ДИНАМИКА механической системы и твердого тела.
Общие теоремы динамики системы.
Теорема об изменении кинетической энергии системы.
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ.
Кинетическая энергия системы.
Опр. Кинетической энергией системы называется скалярная величина Т , равная сумме кинетических энергий всех точек системы.
Т mkVk2 /2. |
(1) |
Кинетическая энергия является характеристикой и поступательного, и вращательного движений системы.
Если система состоит из нескольких тел, то ее кинетическая энергия равна сумме кинетических энергий этих тел.
ВЫЧИСЛЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТЕЛА В РАЗНЫХ СЛУЧАЯХ.
1. Кинетическая энергия при поступательном движении
Все точки движутся с одинаковыми скоростями, равными скорости центра масс Vk = VC . Тогда по формуле (1)
Тпост mkVC2 /2 ( mk )VC2 /2.
Вывод. Кинетическая энергия тела при поступательном |
|
движении равна половине произведения массы тела на |
|
квадрат скорости центра масс. |
(2) |
Тпост М VC2 /2. |
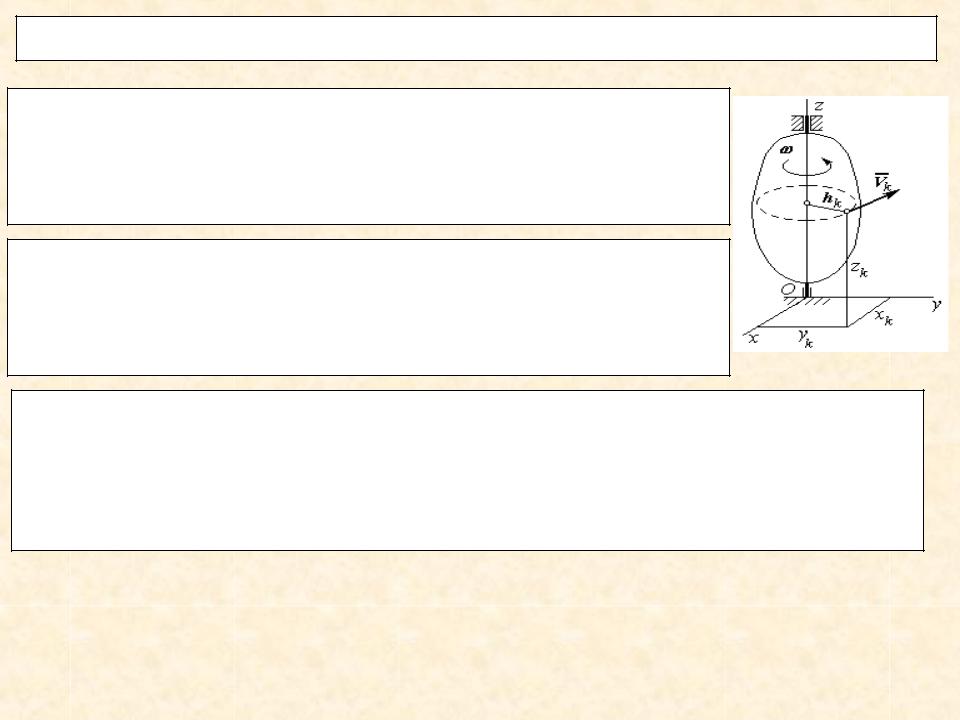
2. Кинетическая энергия при вращательном движении
Если тело вращается вокруг оси Оz, то скорость любой его точки Vk = ω hk, где hk - расстояние
от оси вращения, а ω – угловая скорость тела.
Подставляя это значение в формулу (1) и вынося общий знаменатель за скобки, получим
Твр mk ω2hk2 /2 ( mk hk2 )ω2 /2.
Вывод. Кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела на квадрат его угловой скорости.
Твр J zω2 /2. |
(3) |
3. Кинетическая энергия при плоском движении тела
Кинетическая энергия определяется как при вращательном движении вокруг м.ц.с., т. е. по формуле (3).
VC
900 
С
2 |
/ 2 |
(4) |
Р |
Тпл JР |
z |
||
|
|
|
где JР – момент инерции относительно оси Р z; ω – угловая скорость тела.
По теореме Гюйгенса JР = JC + М d 2, где d = РС. Подставляя это выражение в (4) и учитывая, что ωd = ω РС = VC, получим
Тпл МVC2 / 2 JC ω2 / 2. |
(5) |
Вывод. Кинетическая энергия тела при плоском движении равна энергии поступательного движения со скоростью центра масс, сложенной с кинетической энергией вращательного движения вокруг центра масс.
НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ |
|
||||
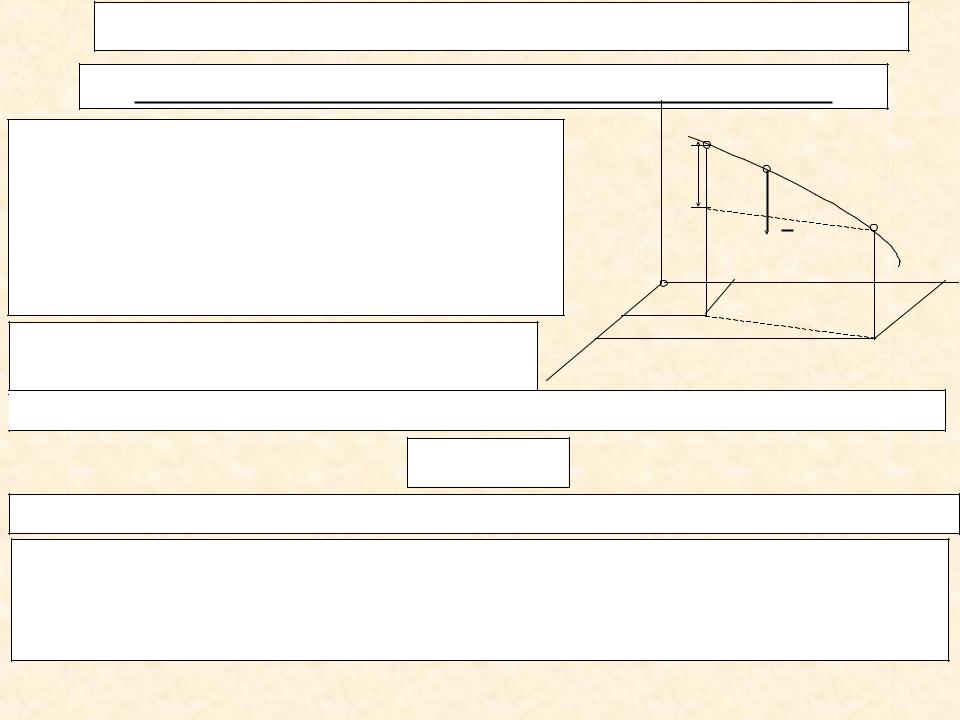
1. Работа сил тяжести, действующих на систему. |
|
|
|||
Работа силы тяжести, действующей |
z |
Мk0 |
|
|
|
|
Мk |
|
|
||
|
hk |
|
|
||
на частицу тела Мk весом рk, равна |
|
|
Мk1 |
|
|
|
z |
|
|
||
рk(zk0- zk1), где zk0 и zk1 – координаты, |
|
k0 |
|
|
|
|
|
Р |
zk1 |
|
|
определяющие начальное и конечное |
О |
хk0 |
|
|
|
положение частицы. |
|
|
|
у |
|
уk0 |
|
|
|||
Тогда, учтя, что рk zk PzC , |
|
хk1 |
|||
х |
уk1 |
|
|
|
|
найдем для суммы работ всех сил |
|
|
|
|
|
тяжести, действующих на систему А рk zk0 |
рk zk1 |
P(zC 0 |
zC1 |
). |
|
А РhC , |
|
|
|
|
|
где Р –вес системы, hC –вертикальное перемещение центра масс.
Вывод. Работа сил тяжести, действующих на систему,
вычисляется как работа их главного вектора |
Р |
на |
перемещении центра масс системы. |
|
|
|
|
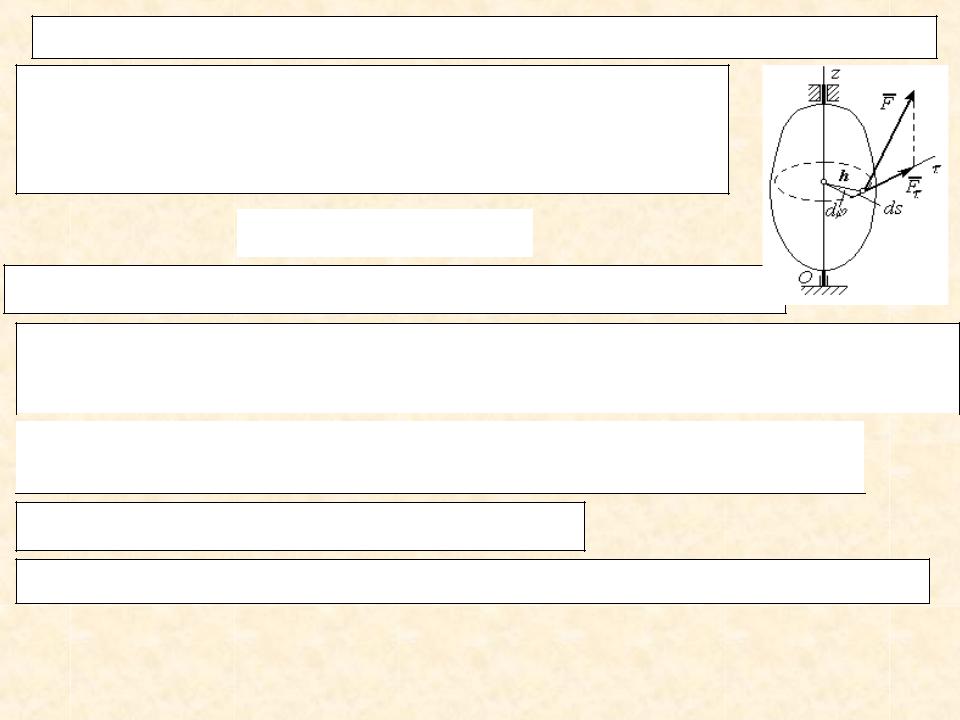
2. Работа сил, приложенных к вращающемуся телу
Элементарная работа силы F определяется по формуле dA = F ds = F h d , так как ds = hd , где
d – элементарный угол поворота тела.
F h = mz ( F). |
(1) |
Величина mZ(F) называется вращающим моментом.
Вывод. Элементарная работа равна произведению вращающего
момента на элементарный угол поворота: dA = Mz d . |
(2) |
|
|
|
|
При повороте на конечный угол А = |
1 |
|
М Z d . |
|
|
|
0 |
|
|
|
|
При постоянном моменте А = Mz 1.
Мощность определится в виде - N = dA/dt = Mz d /dt = Mz ω.
3. Работа сил трения, действующих на катящееся колесо |
|||||
На колесо, катящееся по без |
|
|
|
NQ |
|
скольжения, действует |
|
|
VC |
||
приложенная в точке А сила |
|
С |
|
С |
|
трения |
F . |
|
|
|
k |
тр |
Fтр |
А |
F |
А В |
|
|
|
|
|
|
Р |
Элементарная работа этой силы dA =Fтр dsА. Перемещение |
|||||
dsА= 0, так как точка А совпадает с м.ц.с. Т.е. для каждого |
|||||
перемещения dA = 0. |
|
|
|
|
|
Вывод. При качении без скольжения работа силы трения, препятствующей скольжению, на любом перемещении тела равна нулю.
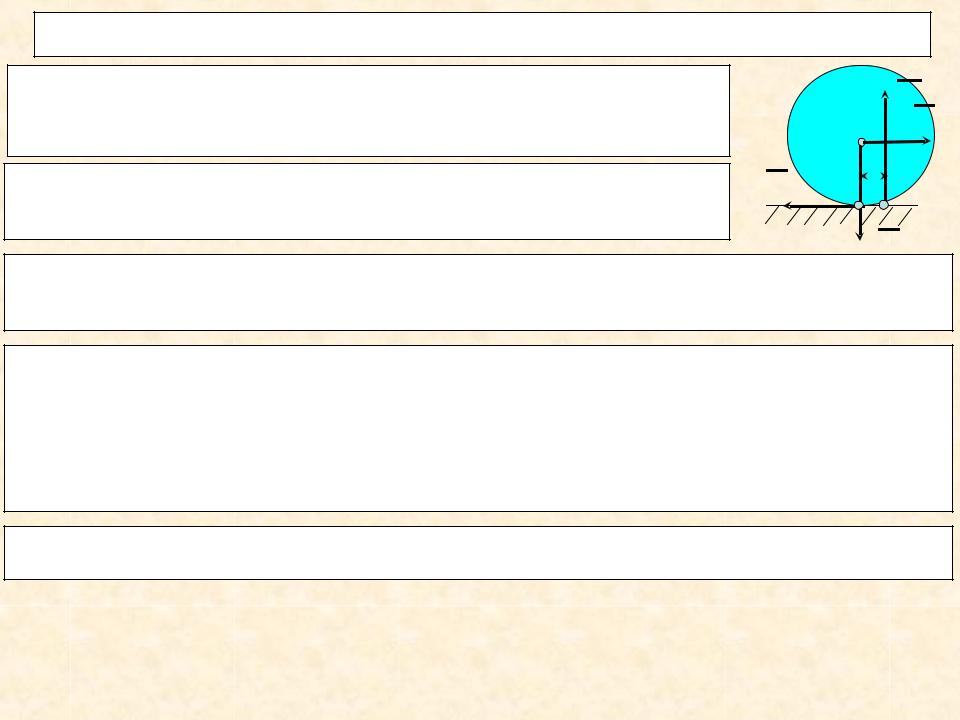
3. Работа сил трения, действующих на катящееся колесо
Сопротивление качению колеса создает |
|
|
|
|
N |
возникающая из-за поверхности пара сил |
N |
и Р. |
С |
k |
Q |
Момент пары М = k ·N, где k – коэффициент |
|
||||
F |
А |
В |
|||
трения качения. |
|
|
|
Р |
|
Вывод 1. |
|
|
|
|
|
|
|
|
|
|
|
Элементарная работа момента пары dAкач = - М кач d = - kN d . |
|||||
Вывод 2.
Работа момента трения1 на конечном1 перемещении1
Акач dAкач M кач d kNd .
0 |
0 |
0 |
Если N = cоnst, то Aкач = - k N φ1 .
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
Рассмотрим какую-нибудь точку системы с массой mk, имеющую скорость Vk.
Для этой точки теорема об изменении кинетической энергии будет иметь вид d(mkVk2/2) =dAek+ dAki,
где dAek и dAki – элементарные работы действующих на точку внешних и внутренних сил.
Составляя такие уравнения для каждой точки системы и складывая их почленно, найдем
d( mkVk2 /2) dAke dAki .
или |
dТ dAke dAki . |
(1) |
Вывод. Равенство (1) выражает теорему об изменении кинетической энергии системы в дифференциальной форме.
Проинтегрировав выражение (1) в пределах, соответствующих начальному и конечному положениям системы, получим
Т1 Т0 Ake Aki . |
(2) |
Равенство (2) выражает теорему об изменении кинетической энергии системы в интегральной (конечной ) форме.
Теорема. Изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и
внутренних сил.
Примечание. В отличие от других теорем внутренние силы в выражениях (1) и (2) не исключаются.