ДИНАМИКА механической системы и твердого тела.
Введение в динамику. Моменты инерции.
МЕХАНИЧЕСКАЯ СИСТЕМА. ВНЕШНИЕ И ВНУТРЕННИЕ СИЛЫ.
Понятие механической системы.
Опр. Систему материальных точек или тел, движение (или равновесие) которой рассматривается называют механической системой.
Внешние и внутренние силы.
Действующие на механическую систему силы разделяют на внешние - Fke и Fki .
Опр. Внешними называются силы, действующие на точки системы со стороны точек и тел, не входящих в состав системы.
Опр. Внутренними называются силы, с которыми точки и тела системы действуют друг на друга.
Свойства внутренних сил.
|
|
|
F i |
А2 |
|
|
|
||
1. Геометрическая сумма (главный вектор) |
|
|
21 |
|
|
|
|
||
всех внутренних сил системы |
|
F12i |
h |
|
i |
|
|
||
равняется нулю Fk 0. |
|
А1 |
|
О |
|
|
|
||
|
|
|
|
|
Доказательство основано на том, что F12i F21i . |
|
|
||
2. Сумма моментов (главный момент) всех внутренних сил
системы относительно любого центра или оси равняется нулю mO(Fki ) 0 и mx(Fki ) 0.
Доказательство основано на том, что F12i h F21i h.
МАССА СИСТЕМЫ. ЦЕНТР МАСС.
Масса системы (обозначатся М или m) равна арифметической сумме масс всех точек (тел), образующих систему: М mk .
Геометрическая точка С, координаты которой определяются формулами:
хС |
1 |
mk xk , |
уС |
1 |
mk уk , |
zC |
1 |
mk zk , (1) |
М |
М |
М |
называется центром масс механической системы.
Если положение центра масс определяется его радиусом –
вектором rC , то |
|
|
1 |
|
|
(2) |
|
rC |
|
mk rk |
, |
||||
М |
|||||||
|
|
|
|
|
|
где rk радиусы – векторы точек, образующих систему.
Для твердого тела, находящегося в поле тяжести, положение центра масс и центра тяжести совпадают.
МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ.
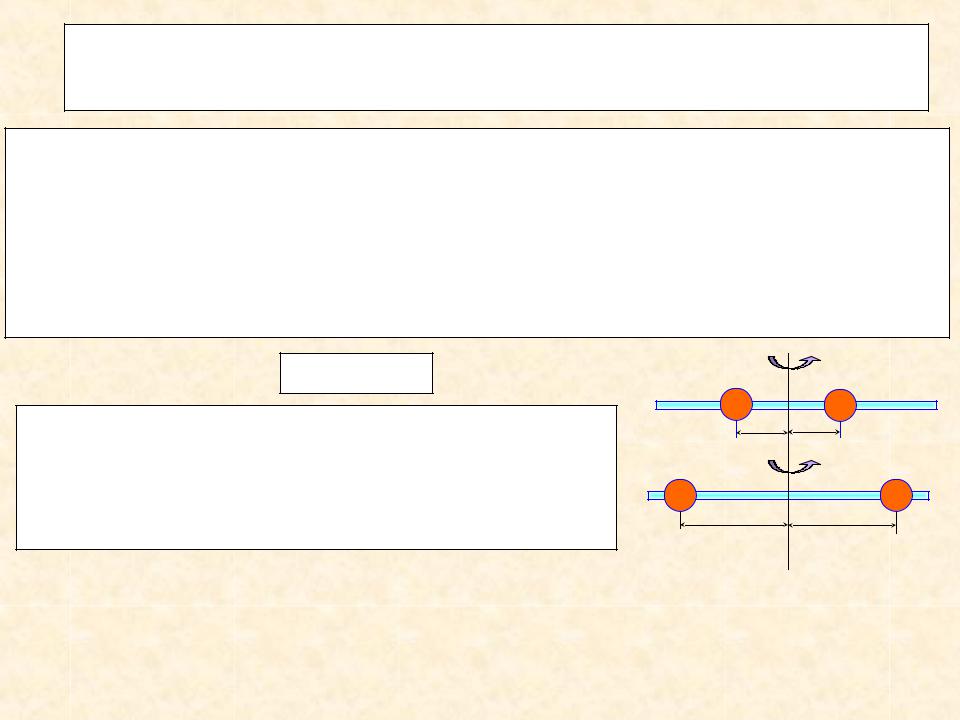
Опр. Моментом инерции тела (системы) относительно данной оси О z (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси:
J Z mk hk2 . |
|
|
(3) |
m2 > m1 |
|
|
m1 |
|
|
|
|
Физический смысл: осевой момент |
|
h1 |
h1 |
инерции является мерой инертности |
|
|
m2 |
тела при вращательном движении. |
h2 |
|
h2 |
|
|
|
Выражение осевых моментов инерции |
|
z |
|
|
|
|
||||
|
|
|
|
|
|||||||
|
через координаты точек системы хk, уk, zk. |
|
|
hk |
|
|
|||||
|
|
|
|
Мk |
|||||||
|
|
|
|
|
|
|
|
|
|
||
Так как h 2 = х 2 |
+ у 2, то |
|
|
|
|
|
|
||||
|
|
|
|
|
|
zk |
|||||
|
k |
k |
k |
|
|
|
|
|
|
||
|
J Z mk ( хk2 уk2 ). |
|
|
|
|
|
|
|
|
||
|
Аналогично |
|
|
(4) |
|
х |
О |
|
хk у |
||
|
Х mk(уk2 zk2 ), |
|
|
|
уk |
|
|
||||
|
J |
|
|
|
|
|
|
|
|
||
|
JУ mk(zk2 хk2 ). |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Опр. Радиусом инерции тела относительно оси Оz называется линейная величина ρz, определяемая равенством
Jz= М ρz2. |
(5) |
Радиус инерции геометрически равен расстоянию от оси Оz той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.
Зная радиус инерции, по формуле (4) можно найти момент инерции и наоборот.
Формулы (3), (4) справедливы как для твердого тела, так и для любой системы материальных точек.
В случае сплошного тела можно получить, что
J |
Z |
h2dm или |
h2dV . |
(6) |
|
|
|
||
|
|
( V ) |
( V ) |
|
Аналогично для сплошного тела формулы (3) примут вид
J |
Х |
|
z2 )dV и т. д. |
(7) |
|
( у2 |
|
( V )
МОМЕНТЫ ИНЕРЦИИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ
1. ТОНКИЙ ОДНОРОДНЫЙ СТЕРЖЕНЬ
Пусть длина стержня l, его масса m.
Вычислим момент инерции относительно оси Аz, ┴ к стержню и проходящей через его конец А.
Направим вдоль АВ координатную ось Ах.
А |
|
z |
|
х
C
dx
Вx
Для любого элементарного отрезка dx величина h = x, а масса dm = ρ1dx, где ρ1 = М / l – масса единицы длины стержня.
|
|
|
|
|
l |
l |
|
|
В результате формула (6) дает J A x2dm 1 |
x2dx 1l3 / 3. |
|
|
0 |
0 |
|
|
|
Заменяя здесь ρ1 его значением, окончательно найдем
JА = М l 2 / 3.
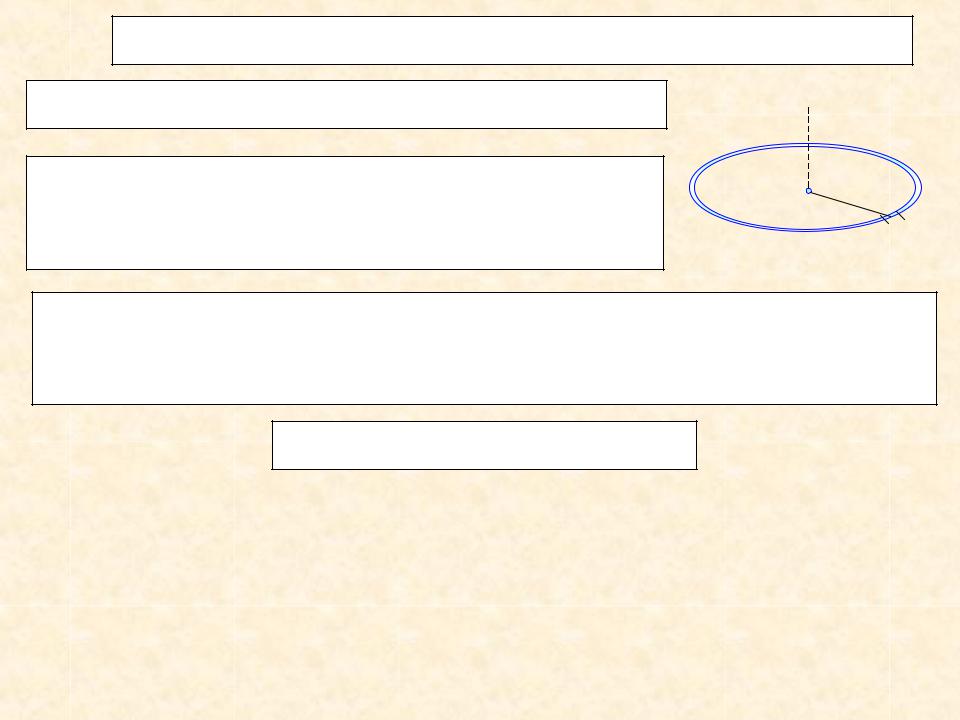
2. ТОНКОЕ КРУГЛОЕ ОДНОРОДНОЕ КОЛЬЦО
Пусть радиус кольца R, его масса m.
Момент инерции относительно оси Cz, перпендикулярной плоскости кольца и проходящей через его центр С.
z
C
R
Так как все точки кольца находятся на оси Сz на расстоянии hk = R, то из формулы (3) JС mk R2 ( mk )R2 M R2 .
Т.е. для кольца JС M R2 .
3. КРУГЛАЯ ОДНОРОДНАЯ ПЛАСТИНКА ИЛИ ЦИЛИНДР
Пусть радиус пластинки R, ее масса m.
Момент инерции относительно оси Cz, перпендикулярной плоскости пластинки и проходящей через его центр С.
R
C
По формуле (6) получим |
JС M R2 / 2. |
|
|