3.2. Среднее и действующее значения синусоидально изменяющейся величины.

Под средним значением, синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Так, среднее значение тока

(3.4)

т. е. среднее значение синусоидального тока составляет 2/= 0,638 от амплитудного. Аналогично, Е_ср=2Е_т/; U_ср=2U_m/.

Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или средне­квадратичным). Действующее значение тока

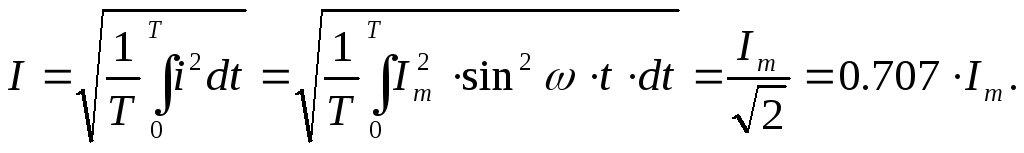(3.5)

Следовательно, действующее значение синусоидального тока равно 0,707 от амплитуды. Аналогично,

Можно сопоставить тепловое действие синусоидального тока с теп­ловым действием постоянного тока , текущего то же время по тому же сопротивлению.

Количество теплоты, выделенное за один период синусоидальным током,

Выделенная за то же время постоянным током теплота равна R I² _пост T. Приравняем их:

или

Таким образом, действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.

Большинство измерительных приборов показывает действующее значение измеряемой величины .

3.3. Коэффициент амплитуды и коэффициент формы.

Коэффи­циент амплитуды k_a — это отношение амплитуды периодически изменяющейся функции к ее действующему значению.

Так, для синусоидального тока

(3.6)

Под коэффициентом формы k_Ф понимают от­ношение действующего значения периодически изменяющейся функции к ее среднему за пол­периода значению. Для синусоидального тока

(3.7)

Иногда пользуются понятием коэффициента формы несинусоидаль­ной функции, определенного следующим образом:

по модулю

где I_ср –среднее по модулю значение тока.

3.4. Изображение синусоидально изменяющихся величин векто­рами на комплексной плоскости. Комплексная амплитуда. Комплекс действующего значения.

На рис. дана комплексная плоскость, на которой можно изобразить комплексные числа. Комплексное число имеет действительную (вещественную) и мнимую части. По оси абсцисс комплексной плоскости откладывают действительную часть комплекс­ного числа, а по оси ординат—мнимую часть. На оси действительных значений ставим +1. а на оси мнимых значений .

И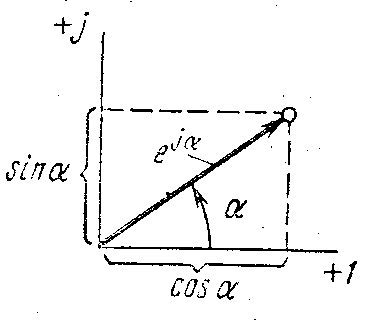з курса математики известна формула Эйлера

(3.8)

Комплексное число e ^ja изображают на комплексной плоскости вектором, численно равным единице и составляющим угол к с осью вещественных значений (осью +1). Угол а отсчитываем против часо­вой стрелки от оси + 1. Модуль функции

П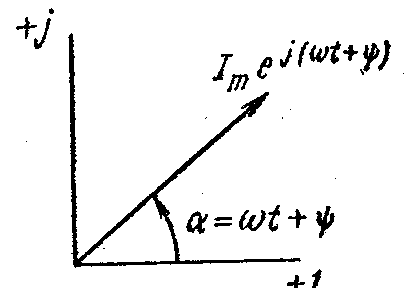роекция функцииe ^ja на ось +1 равна cos a, а на ось +j равна sin а. Если вместо функции e ^ja взять функцию Im e ^ja, то

I_m e ^ja=I_mcosa+jI_msina.

На комплексной плоскости эта функция, так же как и функция e ^ja, изобразится под углом a к оси

+ 1, но величина вектора будет в I_m раз больше.

Угол a в формуле (3.8) может быть любым. Положим, что a=t+ изменяется прямо пропорционально времени. Тогда

I_me ^{j(t+)}=I_mcos(t+)+jI_msin(t+). (3.9)

Слагаемое I_mcos(t+) представляет собой действительную часть (Re) выражения I_me ^{j(t+)}

I_mcos(t+)=Re I_me^{j(t+)} (3.10)

а функция I_msin(t+) есть коэффициент при мнимой части (Im) выражения I_me^{j(t+)}

i= I_msin(t+)=Im I_me^{j(t+)} (3.10a)

Таким образом синусоидально изменяющийся ток i ср. (3.1) и (3.10а) можно представить как Im I_me ^{j(t+)} или, что то же самое, как проекцию вращаю­щегося вектора I_me ^{j(t+)}на ось +j (рис.3.3).

Исторически сложилось так, что в радиотехниче­ской литературе за основу обычно принимают не сину­соиду, а косинусоиду и потому пользуются формулой (3.10).

С целью единообразия принято на комплекс­ной плоскости изображать векторы синусоидально изменяющихся во времени величин для момента времени t=0. При этом вектор равен

I_me ^{j(t+)}= I_me ^j=İ_m , (3.11)

где İ_m — комплексная величина, модуль которой равен I_m;  – угол, под которым вектор İ_m проведен к оси + 1 на комплексной плоскости, равен начальной фазе .

Величину 1_т называют комплексной амплитудой тока i. Комп­лексная амплитуда изображает ток i на комплексной плоскости для момента времени t=0.

Рассмотрим два числовых примера на переход от мгновенного значения тока к комплексной амплитуде и от комплексной амплитуды и мгновенному значению.