1.9. Включение rL-цепи на переменное напряжение

Пусть дана схема (рис 1.36) и параметры:

Определить: i(t) = ?

Начальные условия:

.

Дифференциальное уравнение будет иметь вид:

Общее решение:

i_{св =}.

Корень:

.

После завершения переходного процесса определим принужденный ток комплексным методом по схеме (рис. 1.37):

.

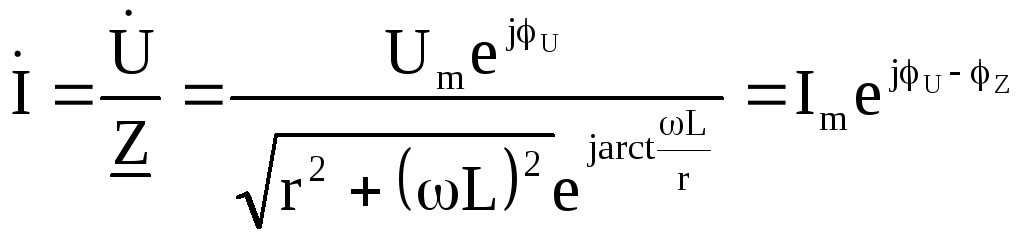Перейдем комплекс тока во временную область:

.

Решение примет вид:

.

При найдем А:

,

отсюда

.

Построим возможный график переходного процесса тока i(t) (рис. 1.38)

1.10. Расчет переходных процессов в цепях с синусоидальными источниками классическим методом

Пусть для цепи (рис. 1.39) дано:.

Определить:

Решение

Начальные условия при :

;

.

Определим эти токи комплексным методом по схеме замещения (рис. 1.40):

.

Тогда при токи равны:

.

Напряжение на конденсаторе:

.

Приt = 0_-

.

По закону коммутации:

.

При t = 0₊ составим схему замещения (рис. 1.41), где .

Составим уравнения законов Кирхгофа:

После решения этих уравнений получаем:

; ;.

Приt →∞ определим принужденные составляющие: .

Для этого составим схему замещения (рис. 1.42). Комплексным методом определим токи и переведем их во временную область:

;

;

.

Находим корень характеристического уравнения. Для этого источник исключаем (рис. 1. 43), ключ оставляем замкнутым.

После преобразований (рис. 1.44), получим сопротивление:

или

,

тогда корень равен:

.

Решение для первого тока:

.

Постоянную интегрирования А найдем при :

;

.

Решение для второго тока аналогично:

;

.

Третий ток найдем по первому закону Кирхгофа:

.

1.11. Расчет переходных процессов при некорректной коммутации классическим методом

Пусть задана схема (рис. 1.45). При размыкании ключа рассмотрим переходный процесс.

Так как при t = 0_- ток первого индуктивного элемента равен: , а второго -, то при размыкании ключа эти токи в первый момент не должны измениться. С другой стороны по закону коммутации:.

Используя обобщенный закон коммутации на индуктивности, найдем ток:;;.

Дальнейший расчет осуществляют обычным классическим методом. Принужденный ток: . Характеристическое уравнение:. Корень:. Решение для тока:. Определение постоянной интегрирования при:,

Если , то

График переходного процесса приведен на рис.1.46

1.12. Решение дифференциальных уравнений методом Эйлера

Возьмем дифференциальное уравнение:

и приведем его к форме Коши: .

Приведем производную к конечным разностям: . Приращение, где к – номер шага,,h – шаг интегрирования, равный постоянной величине. Тогда решение для к+1 шага примет вид: и их первые значения :

к = 1

к = 2

Точность расчета определяется шагом h.

Шаг h связан с постоянной переходного процесса (для рассматриваемого случая).

В настоящее время получил наибольшее распространение в машинных расчетах метод Рунге – Кутта.