Новая папка / Глава 7.3 Метод интеграла Дюамеля

РАЗДЕЛ.

РАСЧЁТ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДОМ ИНТЕГРАЛА ДЮАМЕЛЯ.

Это такой метод, который позволяет рассчитать любой переходный процесс начиная от коммутации и заканчивая любым произвольным воздействием

=

Если Е=1(не вольт а просто 1)

g(t) – переходная проводимость. По ней всегда можно найти i(t)

Если U0=1, то

- переходная функция

ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ ФУНКЦИЙ.

Переходные функции бывают:

1. Неимеющие размерность - h(t).

2. Имеющие размерность – g(t).

Если в эл. цепи в переходном процессе отличном от коммутации требуется найти токи и напряжения в ветвях, то сначала находят передаточные функции в этих ветвях. Для этого любым из известных нам методом рассчитываем процесс включения цепи на напряжение=1.

Найти g1(t), hc(t), g3(t) - ?

А, В и С определяются из начальных условий.

ВЫВОД ФОРМУЛЫ ДЮАМЕЛЯ.

Пусть дано воздействие F

Есть коммутация, линейные законы нарастания и убывания. В первом приближении заменим это воздействие приближенными коммутациями, то есть, заменим F четырьмя коммутациями

Если воздействие не поддаётся аналитическому описанию, то вместо интеграла пользуются суммой Дюамеля. Если же воздействие F описывается одной или несколькими формулами, то пользуются интегралом Дюамеля.

t1 t2 t3

Справедливо в интервале 0 – t1

Имеет смысл с момента t1. Справедливо t1-t2

Справедливо в t2 –t3

Интеграл Дюамеля

ПРИМЕР РАСЧЁТА ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДОМ ИНТЕГРАЛА ДЮАМЕЛЯ.

Найти i(t) - ?, Uc(t) - ?,

Найдём неизвестные величины g(t) - ?, U(t) - ?, h(t) - ?.

1)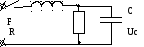

Н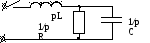 айдём операторным методом

Пользуясь теоремой разложения I(p) переводим в i(t).

При M(p) = 0 p1= 0, p2,3 = из rCLpp + Lp + r = 0. Пусть р2,3 – действительные

Нашли h(t) и g(t).

2) Находим функцию U(t)

Подставляем найденные значения U`(t) и g(t – x) в формулу интеграла Дюамеля, раскрываем его, подставляя пределы. В результате интегрирования получается решение для тока i(t) в промежутке времени от 0 до t1. Верхний предел интеграла – это текущее значение t. Решение справедливо в интервале [0, t].

Если t > t1 , то интеграл будет отсутствовать.

Если t < t1 , то

Вывод 1. То есть решений для каждой из величин будет столько сколькими функциями описывается воздействие.

Вывод 2. При формировании каждого следующего решения предыдущее решение включается в него.