3.7. Первый закон Кирхгофа в операторной форме

По пер­вому закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю. Так, для узла а схемы (рис. 3.5): i₁+i+i₂=0.

Применим преобразование Лапласа и восполь­зуемся тем, что изображение суммы равно сумме изображений. Имеем: I₁(p)+ I(p)+ I₂(p)=0.

В общем случае:

Это уравнение выражает собой первый закон Кирхгофа в операторной форме.

3.8. Второй закон Кирхгофа в опе­раторной форме

Для любого замкнутого контура электрической цепи можно составить уравнение по второму закону Кирхгофа для мгновенных значений. Пред­варительно необходимо выбрать положи­тельные направления для токов в ветвях и направление обхода контура.

Запишем уравнение по второму зако­ну Кирхгофа для контура (рис. 3.7). Кон­тур обходим по часовой стрелке.

Учтем, что индуктивности L₁и L₂имеют магнитную связь. При выб­ранных положительных направлениях для токов i1 и i2 между L₁и L₂имеет место согласное включение.

Падение напряжения на L₁равнона L₂равно

При составлении уравнения учтем, что начальное напря­жение на конденсаторе равно Uc(0). Пусть оно действует согласно с током i₃. Начальное значение тока i₁=i₁(0_-) и тока i₂=i₂(0_-). Имеем:

Каждое из слагаемых заменим операторным изображением:

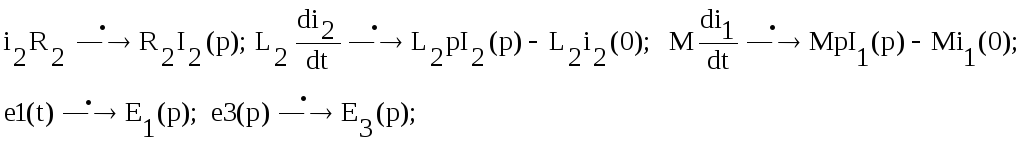
После подстановок, объединим слагаемые с I₁(p), I₂(p), I₃(p). Перенесем в правую часть уравнения Uc(0_-)/p, Li(0_-) и другие внутренние э. д.с. Получим:

I1(p)Z1(p)+I2(p)Z2(p)+I3(p)Z3(p)=E1(p)-E3(p)+E_вн(р),

где Z1(p)=p(L₁-M); Z2(p)=p(M-L₂)-R₂; Z3(p)=; E_вн(p)=(L₁-M)i₁(0)+(M-L₂)i₂(0)-

В общем виде уравнение второго закона Кирхгофа можно переписать так:

.

Это уравнение представляет собой математическую запись вто­рого закона Кирхгофа в операторной форме. В состав E_k(р) в общем случае входят и фиктивные источники начальных условий.

3.9. Расчет переходных процессов операторным методом

Рассчитаем переходный процесс при замыкании ключа в схеме (рис.3.8).

В первую очередь необходимо составить операторную схему замещения. Для этого определим начальные условия на реактивных элементах схемы: u_c1(0_)=E1;i₂(0_)=0;U_c3(0-)=U_c30.

Вводим фиктивные операторные источники начальных условий и составляем операторную схему замещения (рис.3.9).

Составляем уравнения Кирхгофа для расчета операторных токов:

I₁(p) – I₂(p) – I₃(p) = 0

I₁(p)Z₁(p) + I₂(p)Z₂(p)+I₃(p)0 = E₁/p – u_c1(0-)/p +Li₂(0-)

I₁(p) 0 - I₂(p)Z₂(p)+I₃(p)Z₃(p) = -u_c3(0-)/p- Li₂(0-)

Найдем главный определитель:и его алгебраические дополнения:;;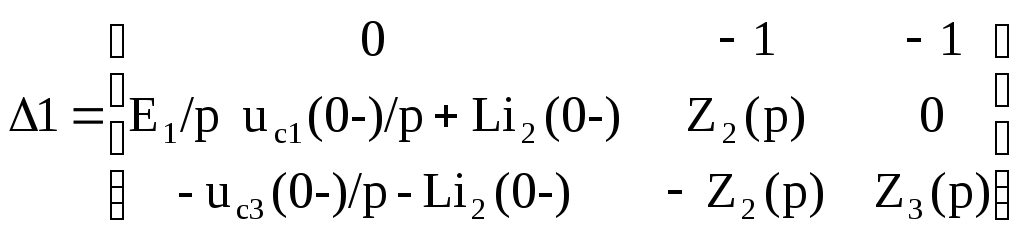

После вычисления определителей получим выражения операторных токов, которые можно представить в виде: I₁(p)=N₁(p)/M₁(p);I₂(p)=N₂(p)/M₂(p);I₃(p)=N₃(p)/M₃(p). Применив к этим решениям теорему разложения можно получить выражения для токов во временной области.

3.10. Расчет переходных процессов операторным методом при действии в цепи синусоидальных источников

Пусть задана схема (рис.3.10) и вид переходного процесса. Напряжение источника имеет вид:

Подвергнем прямому преобразованию Лапласа комплексное напряжение (t), при этом учтём, что:Комплексное напряжениепосле домножения насоставит напряжение источника:. Тогда его изображение равно:

Составим операторную схему замещения (рис.3.11).

Найдём операторное сопротивление Z(p):. Операторный ток источника равен:

Из условия М(Р)=0 находим корни: Производная знаменателя по р равна:.

По теореме разложения находим оригинал этого тока: .