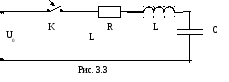
3.3. Включение rL-цепи на постоянное напряжение

Дано: нагрузки r, L, напряжение U₀, схема (рис.3.1) ключ замыкается.

Определить операторный ток I(p) и мгновенный ток i(t).

Решение начнем с начальных условий. Ток индуктивности до замыкания ключа равен: i(0_)=0

Составляем операторную схему замещения электрической цепи (рис.3.2). Ключ замкнут, источник работает наr, L-цепь. Дифференциальное уравнение:

заменяем операторным:. Решаем это уравнение и находим операторный ток:. В знаменателе операторного тока выражение в скобках называютоператорным сопротивлением:

Осталось вернуться из области изображений в область оригинала. Возвращение во временную область осуществляется по теореме разложения или с помощью интеграла Бромвича, если задача не электрическая. Дорешаем эту задачу после рассмотрения теоремы разложения.

3.4. Теорема разложения

Воспользуемся операторным током и запишем его решение в виде дроби:

Если в операторной области решение можно представить в виде отношения двух рациональных дробей, причём (nиm– степени) и если ввести краткое обозначение этих дробейN(P) иM(P), то это отношение дробей можно представить в виде:

,

где: р₁,р₂,р₃… р_m– корни уравнения М(Р)=0, а А₁, А₂…А_к,… А_м– постоянные интегрирования.

Постоянную интегрирования А₁можно определить из условия устремления р, к р₁. Тогда в правой части вместо суммы останется А₁, которую можно определить пределом:

,

где: . Тогда по аналогии для А_к:.

С учётом полученного выражения для А_к, операторный ток примет вид:. Учитывая, что изображениюсоответствует в области оригинала, формула теоремы разложения для оригинала тока примет вид:

Дорешаем задачу (рис.3.1). Числитель и знаменатель операторного тока равны:

N(p)=U0, M(p)=p(r + Lp) . Определим корни уравнения:M(p) = 0 . Первый корень равен:p1=0 , а второй -p2 = -r/L. Найдем производную по р от знаменателя:

. Решение для тока примет вид:

3.5.Фиктивные операторные источники начальных условий

Пусть начальные условия для тока индуктивности i(0_) и напряжения на емкостиu_c(0_) заданы. В области оригинала уравнение процесса в схеме (рис.3.3) примет вид:.

Подвергнем одновременно его левую и правую части преобразованию Лапласа: . Здесьфиктивные операторные источники начальных условий. Их нужно перенести в левую часть уравнения:. Операторная схема замещения примет вид (рис.3.4).

Правило: Фиктивный операторный источник начальных условий включается последовательно с L-элементом и совпадает с направлением тока в нем. Фиктивный операторный источник С-элемента также включается последовательно с ним и имеет направление противоположное току.

3.6. Закон Ома в оператор­ной форме

Пусть задана часть слож­ной разветвленной электрической цепи (рис.3.5). Между узлами а и b этой цепи включена ветвь, содержащая элементы R, L, С и источник ЭДС е (t). Ток ветви обозначим через i .

Замыкание ключа К в схеме приводит к переходному процессу.

До коммутации ток был равен i(0-) и напряжение на конденсаторе u_c(0- ).

Выразим потенциал точки (а) через потенциал точки (b) для после коммутационного режима:

_a=_b+u_c+u_L+u_r-e(t);

u_ab=_a-_b =u_c+u_L+u_r-e(t);

Вместо u_Lзапишем L, вместоu_cзапишемu_c(0_-)+.

Тогда: u_ab=ir+ L+u_c(0_-)+ .

К этому уравнению применим преобразование Лапласа. Преобра­зование Лапласа является линейным, поэтому изображение суммы равно сумме изображений.

Каждое слагаемое уравнения заменим операторным изобра­жением: вместо irзапишемrI(р); вместоu_abзапишем U_ab(p);

L; .

Получим: U_ab(p)=I(p)(R+pL+)-Li(0)+ -Е(р).

Смысл проведенного преобразования состоит в том, что вместо диф­ференциального уравнения получили алгебраическое уравнение, связывающее изображение тока I (р) с изображением ЭДС Е (р) и изображением напряжения U_ab(p). Отсюда сле­дует:

, где Z(p)=R+pL+1/pC представляет собой операторное сопротивление участка цепи между точками а и b. Структура его аналогична структуре комплекса сопротивления того же участка цепи переменному току, если j заме­нить на р.

Комплексное число р = а + jb запишем в виде p = j(b - ja)=j, где=b-jа - комплексная частота, Z (p)=Z (j)- сопротивление, оказываемое рассматриваемой цепью воздействию, подобно тому, как Z (j) есть сопротивление, оказываемое воздействию.

Слагаемое Li(0) представляет собой фиктивный операторный источник начальных условий, обуслов­ленный запасом энергии в магнитном поле индуктивности L вследствие протекания через нее тока i(0) непосредственно до коммутации.

Слагаемое представляет собой фиктивный операторный источник начальных условий, обуслов­ленный запасом энергии в электрическом поле конденсатора вследствие наличия напряжения на немu_c(0) непосредственно до коммутации.

Опера­торная схема замещения участка цепи (рис. 3.5) приведена на рис.3.6.

Рис. 3.6

В частном случае, когда на участке ab отсутствует ЭДС e (t) и к моменту коммутации i(0)=0 и Uс(0)=0 операторный ток имеет более простой вид: I(p)=