2.22. Параллельное включение двух катушек со взаимоиндукцией

Решим следующую задачу:

Дано: схема (рис. 2.30),

Найти: токи и построить векторно-топографической диаграмму.

Решение. Составим уравнения второго закона Кирхгофа. В уравнениях нижний знак (-) выбран для того случая, когда вторая катушка имеет противоположный одноименный зажим.

Главный определитель:

алгебраическое дополнение:

;

ток в первой ветви:

.

Второй ток находится аналогично.

Найдем потенциалы выделенных узлов для построения векторно-топографической диаграммы (рис. 2.30):

Топографическая диаграмма (рис. 2.31) представлена с учетом произвольного выбора токов.

2.23. Расчет цепей переменного тока при наличии взаимоиндукции

Так как напряжения взаимоиндукции учитываются только в уравнениях второго закона Кирхгофа, то при расчете таких цепей применимы все методы, в которых используются уравнения второго закона Кирхгофа. Уравнения второго закона Кирхгофа контуров «к» и «м» для цепей с наличием взаимоиндукции имеют вид :

Линейный трансформатор

Рассмотрим линейный трансформатор (рис. 2.32).

Перейдем от технической схемы к схеме замещения (рис. 2.33).

Решим задачу анализа. Составим уравнения Кирхгофа:

Главный определитель и алгебраические дополнения:

Токи и напряжение нагрузки равны:

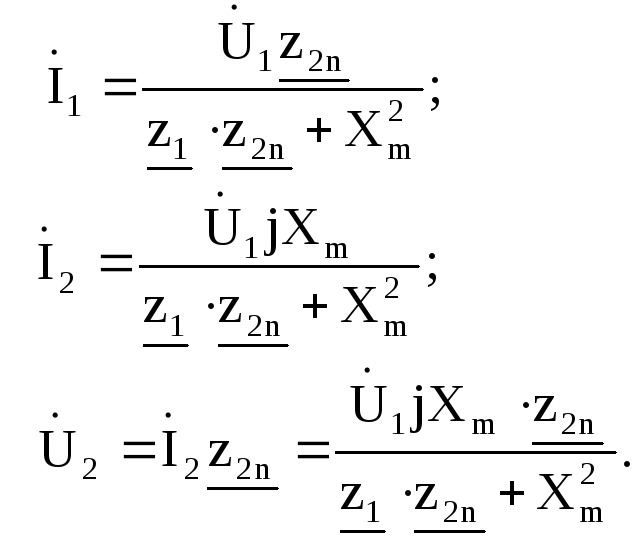
Отношение выходного напряжения к входному называют коэффициентом трансформации:

или через параметры схемы:

.

Еслиk> 1 – трансформатор называют повышающим и еслиk< 1 – понижающим. Более сложные схемы трансформаторов представлены на рис. 2.34. Для тренировки предоставляется возможность самим составить и решить уравнения для этих схем.