2.7. Цепь переменного тока сrL-элементами

Решим задачу:

Дано: u(t) =U_msint;r;L; схема (рис. 2.10).

Найти: напряжение на индуктивности u_L– ? и токi– ?

Решение

Уравнение второго закона Кирхгофа имеет вид: и является дифференциальным уравнением первого порядка. Найти указанные величины можно, но придется решать дифференциальное уравнение. Есть способ решения проще с использованием комплексных чисел.

Использование комплексных чисел в расчетах цепей переменного тока

Представим синусоидально изменяющуюся величину вектором на комплексной плоскости (рис. 2.11,а). Для этого используем формулу Эйлера:

или для амплитуды тока:

.

Так как угол может быть любым, то

Из последней формулы видно, что проекция вращающегося отрезка I_mна мнимую ось, развернутая во времени, равна мгновенному току. Это можно наблюдать по анимационной картинке.Понаблюдайтеэтот процесс, и вам будет понятно это утверждение

Таким образом, если в мгновенный ток подставить момент времени t= 0, то на комплексной плоскости вращающийся отрезок останавливается в начальном положении. Этой информации достаточно для описания любой синусоидальной величины.

Например, ток i= 10sin(t+ 40⁰) на комплексной плоскости (рис. 2.11, б) можно представить вектором:

,

где – комплексная амплитуда тока.

Т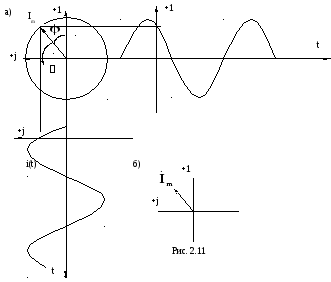еперь дорешаем задачу подраздела 2.7. Дифференциальное уравнениеили с учетом подстановки напряженияприt= 0 в комплексном виде будет иметь вид:

Сопротивление Z=r+jX_Lназывают комплексным.

Закон Ома в комплексной форме записи имеет вид:

.

Его используют для расчета токов в электрических цепях переменного тока. После расчета тока в комплексной форме можно перейти во временную область.

2.8 Цепь переменного тока сRc-элементами

Дано: Электрическая схема (рис. 2.12,а), напряжение источника u=U_msint, активное сопротивлениеr, емкость С.

Найти: комплексный ток в цепи , падения напряжений на элементах,, мгновенный токi(t) , мгновенную мощностьp. Построить топографическую диаграмму напряжений и вектор тока.

Решение

Запишем заданное напряжение и нагрузку в комплексном виде:

По закону Ома комплексный ток равен:

Падения напряжений на элементах цепи можно найти также по закону Ома: .

Второй закон Кирхгофа для схемы (рис.2.12) в комплексном виде примет вид: .

Результаты расчетов можно представить на комплексной плоскости в виде топографической диаграммы напряжений и векторной диаграммы токов. Рассчитаем потенциалы выбранных точек схемы, приняв потенциал точки (а) равным нулю: Используя эти потенциалы, построим топографическую диаграмму напряжений (рис.2.12,б)

Переведем комплекс тока во временную область:

.

Мгновенная мощность равна:

.

2.9. Действующее и среднее значения переменного тока и напряжения

Действующим значением переменного тока или напряженияназывают корень квадратный от интеграла квадрата мгновенных значений тока или напряжения на периоде повторения.

Пользуясь определением, найдем действующее значение синусоидального тока:

После аналогичных вычислений для напряжения получим:

Таким образом, действующие значения переменного тока и напряжения меньше их амплитудных значений в раз.

Действующее значение переменного тока в одной и той же нагрузке rспособствует выделению такой тепловой энергии, которая выделилась бы, если по нагрузке пропустить постоянный ток той же величины.

В комплексном виде действующие значения напряжения и тока имеют вид:

;

Средним по модулю значением напряжения или тока, называют интеграл от модуля мгновенного значения тока или напряжения на периоде повторения.

Найдем среднее значение переменного напряжения:

Средние значения напряжения и тока меньше их амплитудных значений враз. То есть для действующего значения тока:I= 0,707I_m, а для среднего значения тока:I_cp= 0,637I_m.