
устойчивость
.pdf
СОДЕРЖАНИЕ |
|
ВВЕДЕНИЕ |
4 |
1. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ |
|
УПРУГОСТИ |
5 |
1.1.Устойчивость стержня, шарнирно опертого по концам. Формула
Эйлера |
5 |
1.2. Другие случаи закрепления концов |
9 |
1.3.Пределы применимости формулы Эйлера. Равновесные формы в
|
закритической области |
13 |
1.4. Различные критерии устойчивости и методы решения задач |
19 |
|
1.5. |
Приложение принципа возможных перемещений |
23 |
1.6. |
Энергетический критерий устойчивости |
25 |
1.7. Методы Ритца и Тимошенко |
27 |
|
1.8. |
Метод Бубнова-Галеркина |
29 |
1.9.Метод конечных разностей. Упругая шарнирная цепь. Метод
коллокации. Метод последовательных приближений |
30 |
1.10.Применение интегральных уравнений. Приближенное
|
определение первой критической нагрузки |
33 |
1.11. |
Динамический критерий устойчивости |
36 |
1.12. |
Критерий начальных несовершенств |
38 |
1.13. |
Эксцентричное сжатие. Приближенное решение |
40 |
1.14. |
Эксцентричное сжатие. Точное решение |
42 |
1.15. |
Влияние поперечной нагрузки |
44 |
2. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ |
|
|
УПРУГОСТИ. БОЛЕЕ ОБЩИЕ ЗАДАЧИ УСТОЙЧИВОСТИ |
46 |
|
2.1. |
Экспериментальные зависимости |
46 |
2.2. |
Выпучивание стержня при неизменной нагрузке |
48 |
2.3.Влияние формы сечения. Случаи двутаврового и прямоугольного
сечений |
50 |
2.4. Случай сосредоточенной силы в пролете |
51 |
2.5. Действие распределенной продольной нагрузки |
53 |
2.6.Одновременное действие распределенной и сосредоточенной
нагрузок |
56 |
2.7. Устойчивость стержня, связанного с упругим основанием |
58 |
ЗАКЛЮЧЕНИЕ |
61 |
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ |
62 |

В В Е Д Е Н И Е
Расчет на устойчивость, которой посвящен спецкурс, имеет первостепенное значение для элементов конструкций, представляющих собой сравнительно длинные и тонкие стержни, тонкие пластины и оболочки. Напомним основные понятия о видах равновесия.
Равновесие называется устойчивым, если при любом малом отклонении от положения равновесия тело возвращается в исходное положение после устра нения причины, вызвавшей это отклонение. Равновесие называют неустойчи вым, если при любом малом отклонении от положения равновесия тело не воз вращается в исходное положение, а все далее отклоняется от него. При безраз личном равновесии тело, будучи отклоненным, остается в равновесии и в новом положении.
Основы современной математической теории устойчивости движения соз даны в конце XIX в. выдающимся русским математиком и механиком А. М. Ляпуновым. Чтобы иметь представление о том, в чем заключается отли чие приведенных выше определений состояния равновесия от введенного Ля пуновым, сформулируем его применительно к некоторому физическому телу.
Пусть С - произвольное положительное число. Если для любого С, каким бы малым оно не было, можно выбрать такое малое положительное число В (зависящее от С), что при любых начальных отклонениях шарика  от положе-
от положе-
ния равновесия, |
удовлетворяющих условию |
< В, в любой момент времени |
|
выполняется неравенство |
< С, то такое положение равновесия тела устой- |
||
чиво. Здесь под |
подразумевается отклонение тела от положения равновесия |
||
впроцессе его колебательных движений.
Вкурсе сопротивления материалов было изучено устойчивое состояние продольно сжатого стержня сосредоточенной силой. При значении этой силы меньше некоторой критической величины стержень сохранял прямолинейное положение. При достижении этой величины и дальнейшее ее превышение, стержень приобретал криволинейную форму. Расчет критической продольной нагрузки мы проводили путем решения дифференциального уравнения изогну той оси балки, получая известную формулу Эйлера. Необходимо помнить, что эта формула справедлива только в пределах выполнения закона Гука. В других
случаях расчет на устойчивость производился по формуле Ясинского.
Вданном спецкурсе помимо метода Эйлера и Ясинского мы познакомимся
сдругими методиками и принципами расчета критической сжимающей силы и приступим к решению более сложных задач, которые в курсе сопротивления материалов не рассматриваются. Настоящие методические указания составлены по материалам монографии Вольмира А. С. «Устойчивость деформируемых систем» [3].

1. У С Т О Й Ч И В О С Т Ь СЖАТЫ Х С Т Е Р Ж Н Е Й В ПРЕДЕЛА Х
УП Р У Г О С Т И
1.1.Устойчивость стержня, шарнирно опертого по концам.
Формула Эйлера
Определим критическую сжимающую нагрузку для стержня с прямой осью и постоянным по длине поперечным сечением (рис. 1.1.1, а). Пусть один конец стержня О имеет шарнирно неподвижную опору, а второй конец а - шарнирно подвижную. Будем считать, что сжимающая сила Р приложена в центре тяжести сечения и во все время нагружения направлена строго по вер тикали. Расположим оси координат, как показано на рис. 1.1.1.
Рис. 1.1.1. Сжатый стержень, шарнирно опертый по концам
При малых значениях силы Р ось стержня остается прямой и в стержне воз никают напряжения сжатия а=Р/А, где А - площадь поперечного сечения. Когда, постепенно возрастая, сила Р достигнет критического значения, то наря ду с прямолинейной формой равновесия должна иметь место другая, ис кривленная форма, как изображено на рис. 1.1.1, б. Мы предполагаем, что пе реход от прямолинейной формы к изогнутой происходит без изменения вели чины силы Р, т. е. при постоянной длине осевой линии. Но тогда точка а долж на получить некоторое смещение А; можно сказать, что при малых прогибах А пропорционально квадрату стрелы прогиба упругой линии и, таким образом, является величиной второго порядка малости. В дальнейшем на рисунках ус ловно будет приниматься, что точка а вообще не смещается по вертикали.

Выпишем выражение для кривизны изогнутой оси стержня:
(1.1.1)
где / - момент инерции поперечного сечения, М - изгибающий момент в не котором сечении.
Общее выражение для кривизны имеет вид
(1.1.2)
где v - прогиб в сечении х;
Будем считать здесь прогибы малыми по сравнению с длиной стержня.
Изогнутая ось будет тогда пологой |
кривой; считая (dv/dx) « 1 , можно при |
этом принять |
|
|
(1.1.3) |
Изгибающий момент в сечении х |
равен |
 (1.1.4) Получаем дифференциальное уравнение изогнутой оси в виде
(1.1.4) Получаем дифференциальное уравнение изогнутой оси в виде
(1.1.5)
Как видно из рис. 1.1.1, а - б, при изгибе стержня, соответствующим сплош ной линии, прогиб v положителен, а вторая производная отрицательна; таким образом, в уравнение типа (1.1.5) прогиб и вторая производная входят с раз ными знаками. Исходя из этого, мы, независимо от правила знаков для х иМ, приходим к одному и тому же уравнению.
В курсах сопротивления материалов последующее решение задачи ведут исходя из уравнения второго порядка типа (1.1.5). Здесь мы перейдем от (1.1.5) к уравнению четвертого порядка, так как это придаст решению более общий характер и позволит распространить его на другие граничные условия.
Принимая EI=const, продифференцируем (1.1.5) дважды по х; тогда получим:
(1.1.6)
Это соотношение можно также непосредственно получить, исходя из из вестного уравнения упругой линии
(1.1.6а)
вводя фиктивную поперечную нагрузку интенсивностью q. Рассмотрим де формированный элемент стержня, находящийся под действием сжимающих усилий Р (рис. 1.1.2, а); равнодействующая этих усилий, направленная вдоль нормали, будет по рис. 1.1.2, б равна {—Р d2dv/dx2) dx, а величина q равна q=-Pd2v/dx2; отсюда приходим к (1.1.6).
Введем обозначение
(1.1.7)

тогда уравнение (1.1.6) примет вид
(1.1.8)
Однородному линейному дифференциальному уравнению (1.1.6) соот ветствует характеристическое уравнение s2(s2+k2) = 0; корни его равны sx = s2 = 0, s3А = ik. Следовательно, интеграл уравнения (1.1.6) будет
v = A sin кх + В cos кх + Сх + D. |
(1.1.9) |
Рис. 1.1.2. Интенсивность поперечной «нагрузки», вызываемой сжимающими силами
Для решения задачи существенно то обстоятельство, что корни s3 и s4 полу чаются мнимыми; это в свою очередь объясняется тем, что в уравнение типа (1.1.5) величины v и d2v/dx2 входят с разными знаками.
Решение (1.1.9) должно удовлетворять граничным условиям, которые в дан ном случае имеют вид
|
|
(1.1.10) |
Пользуясь этими условиями, находим: |
|
|
B+D= О, В = 0, |
|
|
A sin kl + B cos kl + Cl+ D =0, |
A sin kl+B cos kl =0. |
(1.1.11) |
Отсюда B= С = D = 0. Полагая |
будем иметь |
|
sinkl |
= 0. |
(1.1.12) |
Для аргумента kl получаются значения: |
|
|
kl = |
nn, |
(1.1.13) |
где п - произвольное целое число. Отбрасывая решение kl = 0, как не от вечающее исходным данным задачи, находим:
(1.1.14)
или, по (1.1.6),
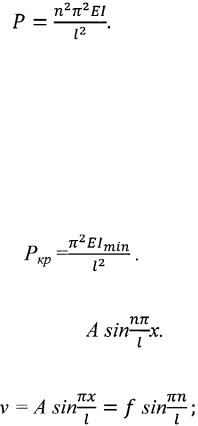
Изменяя число п, получаем последовательный ряд значений силы Р, которым соответствуют различные искривленные равновесные формы.
Под критической силой мы условились понимать силу, при которой прямо линейная форма равновесия стержня перестает быть устойчивой. Следователь но, из всех возможных значений силы надо выбрать наименьшее и принять п=1. Считая, что продольный изгиб произойдет в плоскости наименьшей жест
кости |
стержня, |
будем под |
/ |
понимать |
минимальный момент инерции |
сечения |
7min. |
|
|
|
|
Вводя для критической силы обозначение Ркр, |
получаем: |
||||
|
|
|
|
|
(1.1.16) |
Формула такого вида была получена Л. Эйлером и носит его имя. |
|||||
Вернемся к уравнению изогнутой оси стержня |
|
||||
|
|
v= Asinkx = |
|
(1.1.17) |
|
Мы |
получили |
синусоиду, |
имеющую п полуволн. Критической силе |
||
(при п — 1) соответствует синусоида с одной полуволной: |
|||||
|
|
|
|
|
(1.1.18) |
здесь А |
= f- стрела прогиба. |
|
|
|
|
Принимая последовательно п - 2, 3 и т. д., получим искривленные формы равновесия в виде синусоиды с двумя, тремя и более полуволнами в пределах длины стержня. При этом сила Р будет в четыре, девять и т. д. раз превышать критическую величину.
Эти формы равновесия неустойчивы, но их можно осуществить, если перей ти к новой системе, поставив в точках перегиба синусоиды дополнительные шарнирные подкрепления.
Нами подразумевалось, что сжимающее напряжение в стержне лежит в пре делах действия закона Гука, т. е. не превышает предела пропорциональности материала; следовательно, формулой Эйлера можно пользоваться лишь при этом условии. Напомним также, что мы применяем приближенное выражение (1.1.3) для кривизны изогнутой оси, что является уместным лишь при прогибах, достаточно малых по сравнению с длиной стержня. Именно поэтому величина стрелы погиба f осталась в конечном счете неопределенной. С математической точки зрения рассмотренная нами задача представляет собой задачу о собст венных значениях линейного однородного уравнения типа (1.1.5). Тривиальное решение v = 0 относится к начальному, неискривленному равновесному со стоянию стержня. Нетривиальное решение соответствует так называемым соб ственным функциям задачи, которые в данном случае имеют вид (1.1.17). Пер вая и высшие критические силы (1.1.15) являются собственными значениями параметра Р, входящего в основное уравнение, т. е. такими значениями Р, при которых это уравнение имеет нетривиальное решение, удовлетворяющее всем граничным условиям задачи.
1.2. Другие случаи закрепления концов
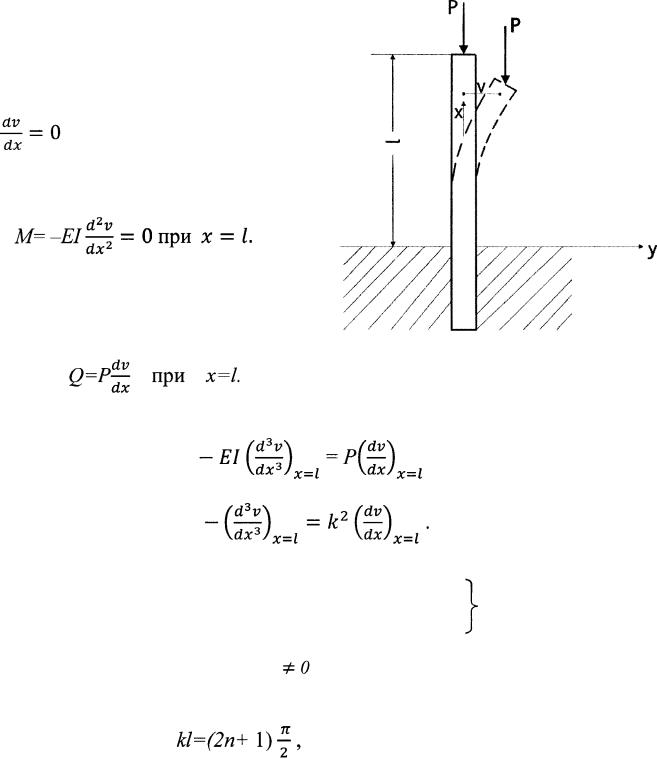
Рассмотрим далее случай, когда один конец стержня защемлен, другой — свободен; сила Р, сохраняющая вертикальное направление, приложена к сво бодному концу (рис. 1.2.1). При потере устойчивости стержень получит прогиб по форме, изображенной на рис. 1.2.1.
Дифференциальное уравнение изо гнутой линии сохраняет вид (1.1.8); об щий интеграл уравнения по-прежнему имеет вид (1.1.9). Выпишем граничные условия. Для защемленного конца имеем: v=0,
п р и х = 0. |
(1.2.1) |
На свободном конце изгибающий мо мент должен обратиться в нуль:
(1.2.2)
Поперечная сила на верхнем конце может быть выражена через силу Р и угол поворота:
Рис. 1.2.1. Стержень, защемленный (1.2.3) одним концом, и со свободным другим
концом
Выражая поперечную силу через прогиб, получим:
|
|
(1.2.4) |
или |
|
|
|
|
(1.2.4 а) |
Используя выписанные условия, находим: |
|
|
B+D = 0, |
Ak+C = 0, |
|
Ак2 sin kl+ Вк2 cos kl = 0, А=0 |
(1.2.5) |
|
Отсюда А = С = 0,В = -D. При В |
будет |
|
cos kl = 0 |
(1.2.6) |
|
и |
n = 0, 1,2,3,... |
(1.2.7) |
Рассуждая так же, как и в предыдущем пункте, находим критическую вели чину силы Р равную (при п - 0)
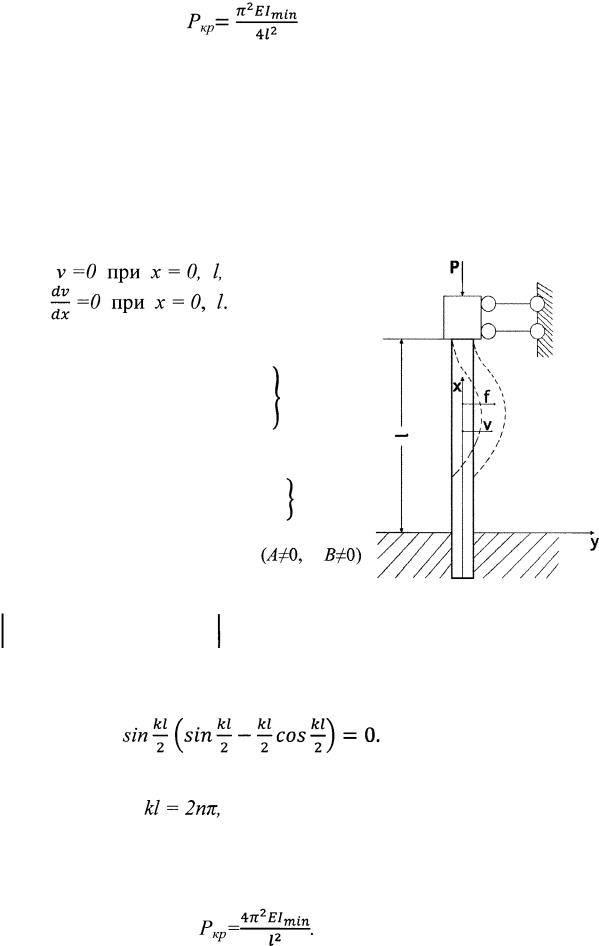
Уравнение изогнутой оси получает вид |
|
|||
|
v = В (cos kx -1). |
(1-2.9) |
||
Если ввести обозначение для перемещения свободного конца, то найдем |
||||
при В = - f |
|
|
|
|
|
v |
= f(l - |
cos kx). |
(1.2.10) |
Примем |
теперь, что один |
конец |
стержня защемлен и |
неподвижен, в то |
время как второй конец защемлен в подвижной опоре (рис. |
1.2.2). Граничные |
|||
условия здесь |
будут: |
|
|
|
(1.2.11)
(1.2.12)
Пользуясь (1.1.9), получаем:
В + D = О, Ак + С = О,
Л sin kl + В coskl + CI + D = О, (1.2.13)
Ak cos kl — Bk sin kl + С = 0.
Для постоянных А, В получаем уравнения
A (sin kl - kl) + В (cos kl |
- 1) |
= |
0, |
(1.2.14) |
|
|||
A(cos kl - 1) - В sin kl |
= |
0. |
|
|||||
|
|
|||||||
Условие нетривиального |
решения |
|
|
|
||||
имеет вид |
|
|
|
|
|
|
|
|
sin kl |
— kl |
cos kl |
— 1 |
= 0. |
(1.2.15) |
Рис. 1.2.2. Стержень с |
||
защемленными концами |
||||||||
cos kl |
— 1 |
—sinkl |
|
|
|
|||
|
|
|
|
|||||
Отсюда для kl находим уравнение |
|
|
|
|||||
|
|
|
|
|
|
|
(1.2.16) |
|
Приравнивая нулю первый множитель, получим: |
|
|||||||
|
|
|
|
|
|
n=1,2, 3,... |
(1.2.17) |
|
Наименьшее возможное значение kl будет равно 2л. Если же приравнять нулю выражение, стоящее в скобках, то наименьший корень будет kl = 8,99. Таким образом, для определения критической силы мы должны положить kl = 2л; тогда

Уравнение упругой линии здесь получает вид (при 2В - —f)
через f по-прежнему обозначена стрела прогиба (рис. 1.2.2).
Наконец, обратимся к случаю, когда нижний конец стержня неподвижно
защемлен, в то время как верхний имеет шарнирную |
опору |
(рис. 1.2.3). |
||||
Граничные условия будут: |
|
|
|
|
|
|
|
v = 0, |
= 0 |
при |
х = О, |
|
|
|
v = 0, |
= 0 |
при |
х = l. |
|
(1.2.21) |
Между постоянными выражения (1.1.9) получим соотношения: |
|
|||||
|
|
В + D = 0, Л/с + С = О, |
|
|||
|
A sin kl + Bcoskl |
+ Cl + D = |
О, |
(1.2.22) |
||
|
|
A sin kl |
+ B cos kl = |
0. |
|
|
При |
- D = В = - Akl, |
С = - Ak будем |
иметь |
|
|
|
|
sin kl - kl cos kl = 0 |
|
|
|||
или |
|
tg kl = kl. |
|
|
|
|
|
|
|
|
|
(1.2.23) |
|
б)
Рис. 1.2.4. Приведенная длина при различных условиях закрепления
Рис. 1.2.3. Один конец стержня защемлен, а другой оперт шарнирно
Наименьшее значение kl, удовлетворяющее этому уравнению, будет

Для критической силы находим выражение
или, с известным приближением,
Г*Р (1.2.26)
~ ,2
Уравнение упругой линии будет
v =A[sin кх - кх + kl(l - cos кх)]. |
(1.2.27) |
На рис. 1.2.4, а - в сопоставлены упругие линии для рассмотренных случаев закрепления. Формулу Эйлера можно записать теперь в обобщенном виде:
(1.2.28)
или
(1.2.29)
Под /о понимается приведенная длина стержня. При произвольных гранич ных условиях ее можно трактовать как длину эквивалентного стержня, имею щего по концам шарнирные опоры. Величину v = l0IL называют коэффициентом приведения длины; он равен отношению длины полуволны синусоиды к дейст вительной длине стержня; на рис. 1.2.4 а - в полуволна синусоиды выделена; здесь же приведены значения v.
Величине Ркр по (1.2.28) соответствует критическое напряжение в попереч ном сечении,равное
(1.2.30)
Обозначим через imin минимальный радиус инерции поперечного сечения:
(1.2.31)
тогда получим:
(1.2.32)
Через 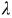 здесь обозначена так называемая гибкость стержня:
здесь обозначена так называемая гибкость стержня:
