5.5. Рекурсия

Рекурсивным называется объект, частично состоя­щий или определяемый с помощью самого себя. Ре­курсия встречается не только в математике, встре­чается она и в повседневной жизни. Кто не видел рекламной картинки, содержащей свое собственное изображение?

В частности, рекурсивные определения представ­ляют собой мощный аппарат в математике.

Примером рекурсии может является вычисление факториала Функция «факториал» n! (для неотрицательных целых чисел) рекурсивно определяется как

0! = 1

n! = n*(n—1)! Еслси n>0

Уравнение вида n! = n*(n-1)! называется рекуррентным соотношением. Рекуррентные соотношения выражают значения функции при помощи других значений, вычисленных для меньших аргументов.

Уравнение Î!=1 — нерекурсивно определенное начальное значение функции. Для каждой рекурсивной функции нужно хотя бы одно такое начальное значение, в противном случае ее нельзя вычислить в явном виде,

Аналогично числа Фибоначчи определяются следующей беско­нечной последовательностью целых чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, . . .. Проверка показывает, что N-í элемент этой последова­тельности равен сумме двух непосредственно предшествующих эле­ментов. Таким образом, значение FIB(N) для N-того числа может быть определено из рекуррентного соотношения:

FIB(N)=FIB(N—1)+FIB(N—2).

Так как FIB(N) определено через два разных значения для мень­ших аргументов, необходимы два начальных значения. Ими служат

FIB(1)=1, FIB(2)=1.

Определенные здесь числа Фибоначчи являются рекурсивным решением следующей задачи:

Каждый месяц самка из пары кроликов приносит двух кроликов (самца и самку). Через два месяца новая самка сама приносит пару кроликов. Нужно найти число кроликов в конце года, если в начале года была одна новорожденная пара кроликов и в течение этого года кролики не умирали,

Эта последовательность названа в честь итальянского математика Фибоначчи, который в 1202 г, сформулировал изложенную здесь задачу.

Функция Аккермана

Две рекурсивные функции, рассмотренные до сих пор, были до­статочно простыми. Поэтому, чтобы не сложилось неправильное впе­чатление о том, насколько сложны рекурсивные функции, представим следующую, довольно простую на первый взгляд, дважды рекурсив­ную функцию, известную как функция Аккермана. Функция дважды рекурсивна, если сама функция и один из ее аргументов определены через самих себя.

N + 1, если М = 0;

А (М, N) = А (М—1, 1), если N = 0;

A [М—1, А (М, N—1)] в остальных случаях.

Беглый просмотр рис. 5.13 показывает, как трудно вычислить эту функцию даже для таких малых аргументов, как М = 4 и N=2. Заметьте, например, что А (4, 1)=A(3, 13).

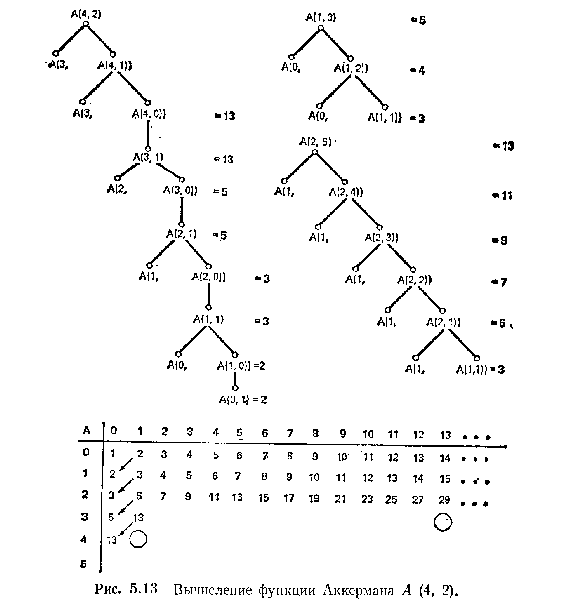
Рис.5.13 Вычисление функции Анкермана А(4,2)

Мощность рекурсивного определения заключается, очевидно, в том, что оно позволяет с помощью ко­нечного высказывания определить бесконечное мно­жество объектов. Аналогично с помощью конечной рекурсивной программы можно описать бесконечное вычисление, причем программа не будет содержать явных повторений. Однако рекурсивные алгоритмы лучше всего использовать, если в решаемой задаче, вычисляемой функции или структуре обрабатывае­мых данных рекурсия уже присутствует явно. В об­щем виде рекурсивную программу Р можно выра­зить как некоторую композицию Р из множества опе­раторов S (не содержащих Р) и самой программы Р:

P = P[S,P]

Для выражения рекурсивных программ необходимо и достаточно иметь понятие процедуры или подпро­граммы, поскольку они позволяют дать любому опе­ратору имя, с помощью которого к нему можно обращаться. Если некоторая процедура Р содержит явную ссылку на саму себя, то ее называют прямо рекурсивной, если же Р ссылается на другую про­цедуру Q, содержащую (прямую и косвенную) ссыл­ку на Р, то Р называют косвенно рекурсивной. По­этому по тексту программы рекурсивность не всегда явно определима.

Как правило, с процедурой связывают множество локальных объектов, т. е. множество переменных, констант, типов и процедур, которые определены - только в этой процедуре и вне ее, не существуют или не имеют смысла. При каждой рекурсивной актива­ции такой процедуры порождается новое множество локальных, связанных переменных. Хотя они имеют те же самые имена, что и соответствующие элементы локального множества предыдущего «поколения» этой процедуры, их значения отличны от последних, а любые конфликты по именам разрешаются с по­мощью правил, определяющих область действия идентификаторов; идентификатор всегда относится к самому последнему порожденному множеству пере­менных. Это же правило справедливо и для пара­метров процедуры, по определению связанных с са­мой процедурой.

Подобно операторам цикла, рекурсивные проце­дуры могут приводить к незаканчивающимся вычис­лениям, и поэтому на эту проблему следует особо обратить внимание. Очевидно основное требование, чтобы рекурсивное обращение к Р управлялось не­которым условием В, которое в какой-то момент ста­новится ложным. Поэтому более точно схему рекур­сивных алгоритмов можно представить в любой из следующих форм;

P º IF В THEN P(S,P) END

или

P ºP (S, IF В THEN P END)

В практических приложениях важно убедиться, что максимальная глубина рекурсий не только конечна, но и достаточно мала. Дело в том, что каждая рекурсивная активация процедуры Р требует памяти для размещения ее переменных. Кроме этих локаль­ных переменных нужно еще сохранять текущее «со­стояние вычислений», чтобы можно было вернуться в него по окончании новой активации Р.

Если взять такой язык как Турбо-Бейсик, то рекурсивными являются подпрограммы: процедура SUB и FUNCTION .

В рекурсивных процедурах реализован принцип "разделяй и властвуй" - сложные алгоритмы разделяются на более простые и решаются. Ниже приведен текст программы для поиска и возврата длины строки.

DECLARE FUNCTION St% (x$)

INPUT "введите строку", in$

PRINT "Длина строки равна", St%(in$)

INPUT a

FUNCTION St% (x$)

IF x$ = "" THEN

REM длина нулевой строки равна 0

St% = 0

ELSE

REM ненулевая строка - рекурсия

REM длина ненулевой строки равна 1 + длина оставшийся части строки.

St% = 1 + St%(MID$(x$, 2))

END IF

END FUNCTION

Рекурсивные алгоритмы особенно подходят для задач, где обрабатываемые данные определяются в терминах рекурсии. Однако это не означает, что та­кое рекурсивное определение данных гарантирует бесспорность употребления для решения задачи ре­курсивного алгоритма. Фактически объяснение кон­цепций рекурсивных алгоритмов на неподходящих для этого примерах и вызвало широко распространен­ное предубеждение против использования рекурсий в программировании; их даже сделали синонимом не­эффективности.

Программы, в которых следует избегать алгорит­мической рекурсии, можно охарактеризовать некото­рой схемой, отражающей их строение. Это следующие схемы:

PºIF В THEN S; Р END

PºS; IF В THEN Р END

Специфично, что в них есть единственное обращение к Р в конце (или начале) всей конструкции.

Такие задачи могут быть решены с помощью простой итерации. Итерация - это последовательное приближение к намеченной цели, когда вычисление нового значения осуществляется циклически, через значения определенные на предыдущем шаге.

Например, вычисление факториала некоторого числа может быть реализовано через рекурсивное решение. Ниже приводится пример такой программы.

DECLARE SUB S (m, f)

INPUT "Введите число", m

m1 = m

CALL S(m, f)

PRINT "Число и его факториал", m1, f

SUB S (m, f)

PRINT f

IF f = 0 THEN f = m

IF m > 1 THEN m = m - 1: f = f * m: CALL S(m, f)

END SUB

Ниже приведен текст программы, когда вычисление факториала можно провести используя итерацию.

INPUT "Введите число", m

m1 = m

IF f = 0 THEN f = m

WHILE m > 1

m = m - 1: f = f * m

WEND

PRINT "Число и его факториал", m1, f

Как видно из примеров, решение задачи для данного случая построенное методом простой итерации более просто и следовательно, более предпочтительнее.

В общем-то программы, построенные по схемам

PºIF В THEN S; Р END

PºS; IF В THEN Р END

нужно переписывать в программы построенные по схемам

Рº(X=Xo; WHILE B S WEND )

Итак, урок таков: следует избегать рекурсий там, где есть очевидное итерационное решение. Однако это не означает, что от рекурсий надо отказываться вообще. Существует много хороших примеров применения рекурсии.

Общий вывод этого раздела состоит в том, что решение задачи может быть проведено как рекурсивно, так и с помощью итераций. А конкретное решение задачи (рекурсия или итерация) зависит прежде всего от построенного алгоритма.