5.3 Программирование с отходом назад

Часто в программировании встречаются задачи в которых необходимо перебрать все возможные комбинации некоторой величины, или ситуация поиска некоторого значения из списка параметров. Встает задача как правильно организовать перебор комбинаций или осуществить поиск, не пропустив при этом ни одного значения. Причем, очень часто складывается ситуацию в которой, при таком переборе необходимо учесть те комбинации на которые условиями задачи поставлен запрет.

Один из методов такой организации вышеназванных процессов является программирование с отходом назад.

Метод разработки алгоритма, известный как программирование с отходом назад, можно описать как организованный исчерпывающий поиск, который часто позволяет избежать исследования всех возмож­ностей.

Этот метод особенно удобен для решения задач, требующих проверки потенциально большого, но конечного числа решений.

Для более полного представления этой задачи ее целесообразно посмотреть на примере задачи о замке с шифр.

Задача о замке

В качестве примера рассмотрим комбинационный замок допустим для вело­сипеда, состоящий из набора N переключателей, каждый из которых может быть в положении «вкл» или «выкл». Замок открывается только при одном наборе положений переключателей, из которых не менее [N/2] (целая часть от N/2) находятся в положении «вкл». Предпо­ложим, что мы забыли эту комбинацию, а нам надо отпереть замок. Предположим также, что мы готовы перепробовать (если необходимо) все комбинации. Нам нужен алгоритм для систематического генери­рования этих комбинаций. Если проигнорировать условие [N/2], то для замка существует 2^N возможных комбинаций. Однако условие [N/2J позволит отбросить (или лучше не генерировать) многие комбинации.

Промоделируем каждую возможную комбинацию вектором из N нулей и единиц. На i-м месте будет 1, если i-й переключатель нахо­дится в положении «вкл», и 0, если i-й переключатель — в положении «выкл». Множество всех возможных N-векторов хорошо моделируется с помощью двоичного дерева. Каждая вершина k-го уровня этого дерева будет соответствовать определенному набору первых k компонент N-вектора. Две ветви, идущие вниз из вершины этого уровня, соответствуют двум возможным значениям (k+1)-й компоненты в N-векторе. У дерева будет N уровней. Рис. 5.5 на примере N=4 поясняет основную конструкцию.

Условие, заключающееся в том, что число переключателей в положении «вкл» должно быть не меньше [N/2], позволяет нам не образовывать части дерева, которые не могут привести к правильной комбинации. Например, рассмотрим вершину 00 на рис. 5.5. Так как правая ветвь (к 000) не может привести к допустимой комбинации, нет нужды ее формировать. Если какие-то вершины, следующие за рассматриваемой вершиной, не удовлетворяют ограничению задачи, то эти вершины не надо рассматривать. В данном случае никакие из вершин, находящихся внутри пунктирных линий, не нужно исследо­вать и даже формировать.

Теперь, воспользовавшись этой моделью двоичного дерева, можно изложить процедуру отхода назад для образования только тех ком­бинаций, в которых по крайней мере [N/2] переключателей нахо­дятся в положении «вкл». Алгоритм сводится к пересечению дерева.

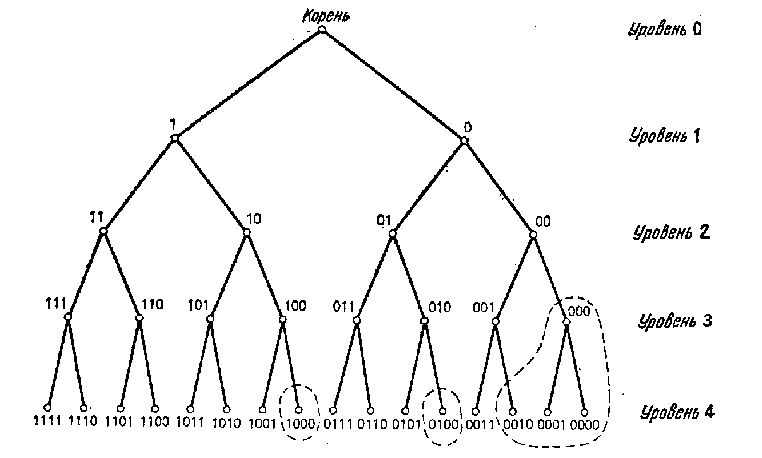
Рис. 5.5 Двоичное дерево, представляющее N-векторы из нулей и единиц.

Двигаемся вниз по дереву, придерживаясь левой ветви, до тех пор, пока это возможно. Достигнув конечной вершины, опробуем соот­ветствующую комбинацию.. Если она не подходит, поднимаемся на один уровень и проверяем, можем ли мы спуститься опять по другой ветви. Если это возможно, берем самую левую из неисследованных ветвей. Если нет, отходим вверх еще на один уровень и пытаемся спуститься из этой вершины. Перед спуском проверяем, можно ли удовлетворить условие об [N/2] включенных переключателях в последующих вершинах. В ситуации, изображенной на рис. 5.5, этот алгоритм просмотрит следующую последовательность вершин:

0001

0011

0111

1111 Проверка этой комбинации.

0111 Отход, так как 1111 —конечная вершина.

1110 Спуск по единственной непросмотренной ветви вниз, про­верка этой комбинации.

0111 Снова отход.

0011 Отход дальше, так как из 0111 все ветви просмотрены.

0110 Спуск по единственной непросмотренной ветви.

1101 Проверка комбинации.

0110 Отход из 1101

1100 Проверка комбинации.

0110 Отход из 1100.

0011 Отход, так как все ветви просмотрены.

0001 Отход, так как все ветви просмотрены.

0010 Спуск по единственной непросмотренной ветви.

0101 Спуск по самой левой непросмотренной ветви.

1011 Проверка комбинации.

0101 Отход.

1010 Проверка комбинации.

0101 Отход.

0010 Отход.

0100 Спуск по единственной непросмотренной ветви.

1001 Проверка комбинации.

0100 Отход.

0010 Отход; заметим, что мы не опускаемся к 1000, так как эта вершина нарушает условие о том, что должно быть по край­ней мере две единицы.

0001 Отход.

Корень Отход.

0 Спуск по единственной непросмотренной ветви.

.

.

.

и т. д.

Алгоритм останавливается, когда мы возвращаемся к корню и не остается непросмотренных ветвей.

Этот простой пример иллюстрирует основные свойства, общие для всех алгоритмов с отходом назад. Если можно сформулировать задачу так, что все возможные решения могут быть образованы построением N-векторов, тогда ее можно решить при помощи процедуры с отходом.