Министерство сельского хозяйства Российской Федерации

Департамент научно-технологической политики и образования

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Красноярский государственный аграрный университет»

Институт экономики и финансов АПК

Кафедра Бухгалтерского учета и статистики

Эконометрика

ЛАБОРАТОРНАЯ РАБОТА №1

Вариант 22

Выполнил

студент группы 39-1, _____________ Шевцова Н.Н.

080101.65 «Экономическая

безопасность»

Очной формы обучения

Принял

к.т.н., доцент _____________ Калягина Л.В.

Красноярск 2014

Район	Потребительские расходы на душу населения, тыс. руб., у	Денежные доходы на душу населения, тыс.руб., х
Северный
Респ. Корелия	596	913
Респ.Коми	417	1095
Архангельская обл.	354	606
Вологодская обл.	526	876
Мурманская обл.	934	1314
Северо-Западный
Ленинградская обл.	412	593
Новгородская обл.	525	754
Псковская обл.	367	528
Центральный
Брянская обл.	364	520
Владимирская обл.	336	539
Ивановская обл.	409	540
Калужская обл.	452	682
Костромская обл.	367	537
Московская обл.	328	589
Орловская обл.	460	626
Рязанская обл.	380	521
Смоленская обл.	439	626
Тверская обл.	344	521
Тульская обл.	401	658
Ярославская обл.	514	746

Построим поле корреляции- совокупность точек результативного и факторного признаков . Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс - индивидуальные значения факторного признака X.

.

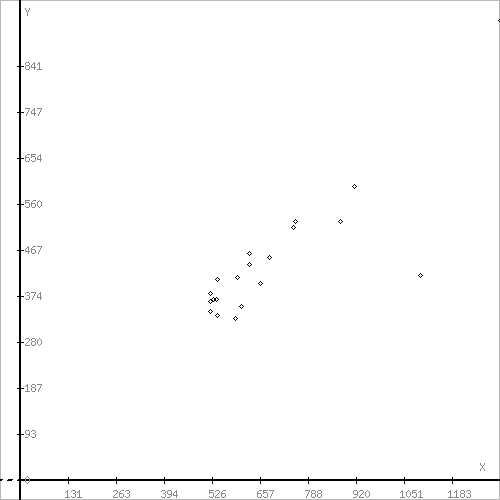
На основании поля корреляции можно выдвинуть гипотезу о том, что связь между всеми возможными значениями X и Y носит линейный характер. Линейное уравнение регрессии имеет вид y = bx + a Оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε. Для оценки параметров а и b - используют МНК (метод наименьших квадратов). Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии.

Для расчета параметров регрессии построим расчетную таблицу (табл. 1)

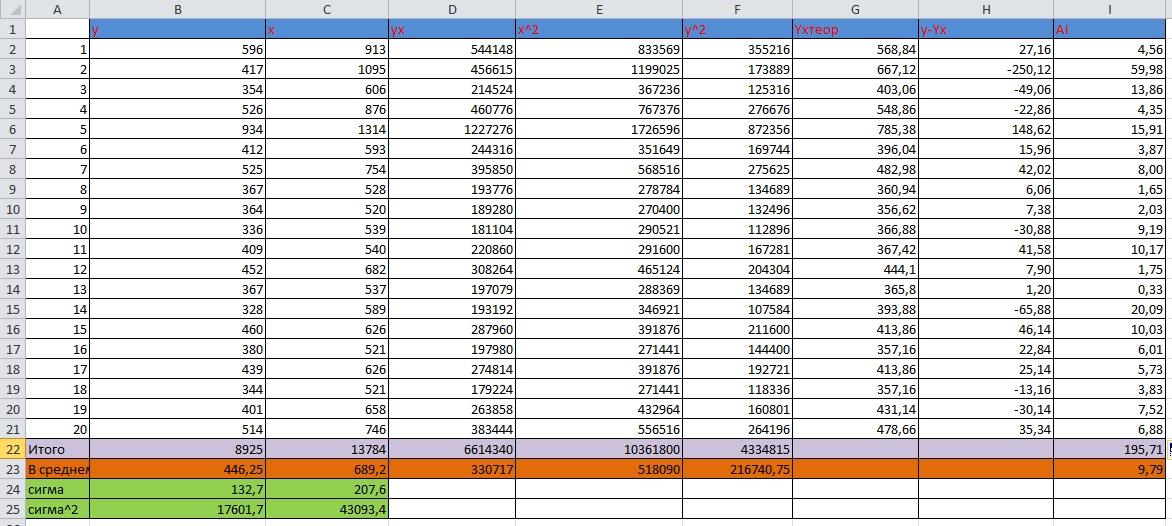табл.1 Расчетная таблиц Система нормальных уравнений. a•n + b∑x = ∑y a∑x + b∑x² = ∑y•x Для наших данных система уравнений имеет вид 20a + 13784 b = 8925 13784 a + 10361800 b = 6614340 Домножим уравнение (1) системы на (-689.2), получим систему, которую решим методом алгебраического сложения. -13784a -9499932.8 b = -6151110 13784 a + 10361800 b = 6614340 Получаем: 861867.2 b = 463230 Откуда b = 0.5375 Теперь найдем коэффициент «a» из уравнения (1): 20a + 13784 b = 8925 20a + 13784 • 0.5375 = 8925 20a = 1516.48 a = 75.8239 Получаем эмпирические коэффициенты регрессии: b = 0.5375, a = 75.8239 Уравнение регрессии (эмпирическое уравнение регрессии): y = 0.5375 x + 75.8239 Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов β_i, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.