Глава 2. Динамика материальной точки.

Первый закон Ньютона

постулирует существование инерциальных систем отсчета (ИСО):

Имеются такие СО, называемые инерциальными, в которых тело не испытывающее воздействия со стороны других тел, находится в состоянии покоя или равномерного прямолинейного движения.

Если одна система инерциальная то другая, движущаяся относительно нее с постоянной скоростью, тоже инерциальная.

Ответ на вопрос, является ли данная СО инерциальной, дает эксперимент.

СО связанная с Землей не является инерциальной, поскольку она движется с постоянным ускорением, вследствие вращения. Но в определенных задачах ее можно считать инерциальной, если точность измерений не высока и мы можем пренебречь эффектами, возникающими из-за вращения Земли.

Масса и импульс.

Состояние тела связано со скоростью. Изменение состояния происходит при взаимодействии тел. Результат взаимодействия зависит от меры инертности тела, в качестве которой выступает масса тела. При взаимодействии двух тел тело с меньшей массой больше изменяет свою скорость, а тело с большей массой меньше изменяет свою скорость. Состояние тела, имеющего скорость и массу, характеризуется величиной, называемойимпульс:

Второй закон Ньютона

связывает получаемое изменение состояния с количественной мерой взаимодействия – силой:

.

При решении задач о движении тела с постоянной массой II Закон Ньютона можно использовать в виде:

,

что представляет собой дифференциальное уравнение для нахождения скорости. Если , то итакже величина постоянная. Тогда удобнее Второй закон Ньютона записывать в виде:

О чем же говорит нам Второй закон Ньютона?

1. Если , тои – совпадают по направлению.

2. Чтобы телу массой придать ускорениенужно приложить силу, равную. Или:скорость изменения импульса равна приложенной к телу силе.

3. II Закон Ньютона связывает различные физические величины, из которых масса, время и расстояние измеряются по сравнению с эталоном. При произвольном выборе единиц измерения силы в этом законе должен появиться коэффициент , связывающий единицы измерения:. Но если положить=1, тов качестве единицы измерения силы мы будем использовать такую силу, которая телу, массой один килограмм сообщает ускорение в один метр в секунду в квадрате; эта единица называется ньютон.

4. В большинстве реальных ситуаций на тело действует не одна, а несколько сил:, Во втором законе Ньютона

–равнодействующая всех сил, действующих на данное тело.

Силы и взаимодействия.

Сила – количественная мера взаимодействия.

Почему и каким образом тела взаимодействуют друг с другом?

Природа взаимодействий сводится к четырем различным видам:

1.Гравитационное

2.Электромагнитгое

3.Сильное

4.Слабое

Сильное взаимодействие – удерживает в одном ядре нейтроны и положительно заряженные протоны (то есть это взаимодействие более сильное, чем кулоновское).

Слабое взаимодействие проявляется при распаде элементарных частиц.

В классической механике 3 и 4 не проявляются, все взаимодействия сводятся к 1 и 2.

1: Притяжение небесных тел и сила тяжести – это проявление гравитационного взаимодействия

2: К электромагнитному взаимодействию кроме силы Кулона, силы Ампера и т. п. относятся также сила упругости и сила трения, поскольку они сводятся к межатомному взаимодействию. А взаимодействие между атомами это взаимодействие между заряженными частицами, то есть электромагнитное.

Сила упругости

Сила упругости подчиняется закону Гука

, – коэффициент жесткости; [] =.

Взаимосвязь деформации и возникающей при этом

Силы можно записать, используя другие величины:

Если величина деформации , а– внутреннее напряжение (нормальное напряжение), то, учитывая, чтоx в законе Гука это то же самое, что Рис 6. Сила и Δl, а значит x=εl, получаем: , где величина упругости

,

которая зависит только от свойств материала, называется модуль Юнга

Сила трения.

Различные виды трения:

При относительном движении соприкасающихся поверхностей твердых тел– сухое трение

При относительном движении твердого тела и жидкости - вязкое трение.

И при относительном движении твердого тела в газовой среде – вязкое трение и сила сопротивления

Сухое трение может проявляться как сила трения покоя или сила трения скольжения.

Сила трения покоя не позволяет соприкасающимся поверхностям смещаться относительно друг друга, противодействуя приложенной силе. Выполняется равенство . Направлена сила трения покоя против приложенной силы. А величина ее может изменяться в пределах от 0 до.(– сила реакции опоры),µ- коэффициент трения. Трение покоя уравновешивает силу, стремящуюся сдвинуть одно тело относительно другого.

Сила трения скольжения возникает, когда два тела двигаются относительно друг друга. Сила трения скольжения равна максимальному значению силы трения покоя:

и направлена против направления движения.

mg

–препятствует движению Рис 7. Сила трения

–обеспечивает движение скольжения

Вязкое трение – осуществляется между твердым и жидким, или между двумя телами с жидкой прослойкой.

,

–коэффициент вязкого трения. Чем меньше скорость, тем меньше сила.

Сила сопротивления (газовая среда).

()

Третий закон Ньютона:

При взаимодействии двух тел сила, действующая на второе со стороны первого, ровна по модулю и противоположна по направлению силе, действующей на первое со стороны второго. (Сила действия равна силе противодействия):

Рис 8. Взаимодействие двух тел.

Принцип относительности Галилея.

Преобразования координат при переходе из одной ИСО в другую .

Если при штриховая и нештриховая ИСО совпадают

(),

и если скорость штриховой ИСОпостоянна и

направлена вдоль оси Ox, то в какой-то момент вре

мени для координат, измеренных в этих ИСО

выполняются следующие равенства:

Рис9. Инерциальные Эти преобразования координат называются

системы отсчёта преобразования Галилея.

Пользуясь ими можно получить формулы

преобразования скорости и ускорения:

=>.

Полученный результат говорит о том, что в обеих ИСО II закон Ньютона записывается совершенно одинаково:

–в штриховой ИСО,

- в нештриховой ИСО

Принцип относительности Галилея:

Все законы механики при переходе из одной ИСО в другую не меняют своего вида, то есть инвариантны по отношению к преобразованию координат.

Сформулированный принцип относительности (инвариантности законов механики) позволяет сделать два важных вывода:

Первый: Никакой эксперимент в области механики, проведенный в пределах одной ИСО не позволит определить скорость этой системы.

И второй: Не существует абсолютной системы отсчета. То есть законы механики не позволяют нам обнаружить ИСО, которая является безусловно покоящейся, и определять некоторую абсолютную скорость движения. Скорость всегда относительна.

В дальнейшем эти выводы были обобщены Эйнштейном на электромагнитные и оптические явления, в результате чего появилась специальная теория относительности.

Закон сохранения импульса

Рассмотрим систему взаимодействующих тел. Учтем, что на каждое тело действуют силы со стороны всех остальных тел, а также сила со стороны внешних (находящихся за пределами системы) тел.

по II Закону Ньютона:

Рис.10 Взаимодействие тел. На рисунке указаны силы,

действующие только на первое тело. Таким же образом

следует учесть силы, действующие на остальные тела

Сложив левые и правые части равенств, получим:

Учитывая, что согласно третьему закону Ньютона ,и так далее, получим:

И если - суммарный импульс всей системы материальных точек, то для него выполняется условие:

Если окакжется,что =0, то система называетсязамкнутой и тогда для суммарного импульса можно записать: или: .

Несмотря на взаимодействие между телами замкнутой системы суммарный импульс замкнутой системы изменяться не будет.

Закон сохранения импульса (ЗСИ):

Суммарный импульс в замкнутой системе сохраняется.

Кинетическая энергия

Согласно второму закону Ньютона .

Умножив это соотношение на равенство , после ряда преобразований получим:

.

Под знаком дифференциала в скобках оказалась величина, которая не будет изменяться при равенстве нулю левой части.

то есть, если , то

Здесь – вектор, модуль которого равен(бесконечно малой часть пути), а направление совпадает с направлением скорости.

Если , то

Эта величина: (или)

Называется кинетическая энергия. .

Если ≠ 0, то,и при переходе из состояния (1) в состояние (2)

,

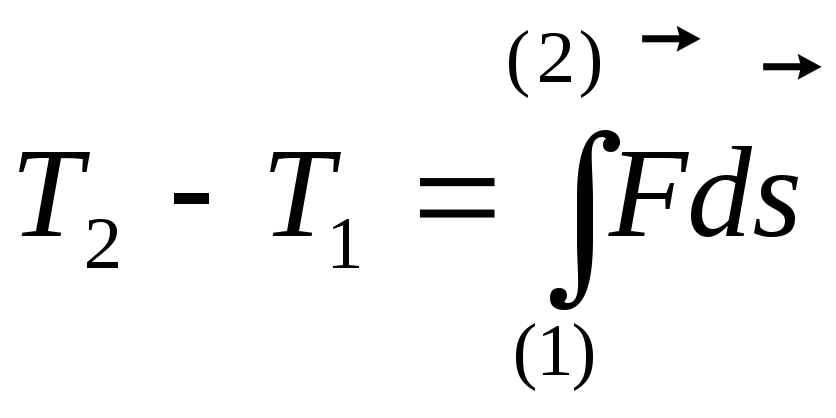где интеграл называетсяработа.

.

Этот результат представляет собой теорему об изменении кинетической энергии:

Изменение кинетической энергии тела равно работе равнодействующей всех сил приложенных к этому телу.

Работа сил

Если - равнодействующая сил, приложенных к данному телу, то интеграл, определяющий работу равнодействующей превращается в сумму интегралов:

то есть мы имеем право говорить о работе отдельной силы .

Работа силы находится как результат интегрирования скалярного произведения, гдеα- угол между векторамии. При вычислении работы можно также использовать вектор. Действительно, на бесконекчно малом участке траектории, где–дуга, а - хорда получим, что при Δдуга окажется равной хорде. (см. рис 11)

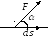
.. Значит работа может быть со-

считана с помощью интеграла:

.

Это говорит о том, что подынтегральное

вы ражение можно представить как

.

Работа не совершается и кинетическая

Рис 11. энергия не изменяется при выполнении

К определению работы одного из трех условий:

; ; .

В частности, не совершает работу сила гравитационного притяжения при движении спутника (или планеты) по круговой орбите, так как в этом случае .

Пример расчета работы: работа силы упругости.

Рис 12. Работа силы упругости

Если мы растягиваем пружину, сила упругости противодействует этому процессу, и работа силы упругости отрицательна. Если растянутая пружина сжимается под действием силы упругости, то работа этой силы будет положительной.

Всегда отрицательной будет работа силы трения, потому что она направлена против движения: α = π и .

Мощность

Мощность – это скорость совершения работы.

Средняя мощность: , где

A₁₂ – работа, совершаемая за интервал времени Δt_{12 .}

Мгновенная мощность: ,где

- бесконечно малая часть работы, приходящаяся на интервал времени dt

Поле сил. Потенциальная энергия.

Поле сил – если каждой точке пространства сопоставить какую-то силу , то мы будем считать, что задано поле сил.

Если сила не зависит от времени , то соответствующее ей поле называетсястационарным.

Если сила во всех точках рассматриваемого пространства одинакова и зависит только от времени , то соответствующее ей поле называетсяоднородным

Будем считать, что имеется некоторое поле сил, заданное функцией , которая связана с вектором силы соотношением:

, то есть . Тогда работа по перемещению тела из точки «1» в точку «2» равняется:

Рис 13. К расчету работы То есть А = П₂ - П₁ — работа равняется

в градиентном поле разности значений функции, задающей поле

в начальной и конечной точках.

Поле, у которого не зависит от формы и длинны пути, а зависит от функции начального и конечного состояния называетсяградиентным (потенциальным). Следует отметить, что величина имеет размерность энергии, и связана с изменением кинетической энергии. Действительно, с одной стороны по теореме об изменении кинетической энергии:

,

с другой:

Введем величину обратную по знаку:; тогда:

.

Это соотношение означает, что уменьшение величины вызывает увеличение кинетической энергии, а увеличениесвязано с уменьшением кинетической энергии. То есть некоторый запасможет превратиться в кинетическую энергию и наоборот. Поэтому эта величина называетсяпотенциальной энергией.

–потенциальная энергия зависит от положения тела в пространстве.

. Сохраняющаяся в градиентном поле сумма кинетической и потенциальной энергий:

,

называется механической энергией.

Взаимосвязь потенциальной энергии и силы, действующей на тело в градиентном поле, определяется по соотношениям:

— разность потенциальных энергий.

Абсолютное значение потенциальной энергии:

определяется с точностью до постоянной, которая зависит от выбора нулевого уровня. Это не имеет решающего значения, поскольку нам важно знать не абсолютное значение потенциальной энергии, а разность потенциальных энергий, которая равна работе сил этого поля:

.