4.3.2. Критерий устойчивости Михайлова

Он был сформулирован А. В. Михайловым в 1936 году и базируется на принципе аргумента. При этом для анализа устойчивости рассматривается характеристический комплекс системы F(jw), который получается из характеристического полинома

(4.16)

заменой p на и имеет вид:

, (4.17)

где можно выделить вещественную и мнимую часть, а также амплитуду и фазу:

(4.18)

Для конкретного численного значения характеристический комплекс представляет собой комплексное число F(j, которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой

При изменении от 0 до конец вектора F(j) выписывает на комплексной плоскости некоторую кривую, которую называют годографом Михайлова. Причем начинается годограф, как следует из соотношения (4.17), в точке с координатами{; j0}.

Рис. 4.8. Вид годографа Михайлова.

Формулировка критерия. Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении от 0 до начинался на вещественной оси в точке и проходил последовательно против часовой стрелки n квадрантов, не обращаясь в ноль и стремясь к в n-ом квадранте.

Доказательство

Утверждение основано на расположении годографа Михайлова на комплексной плоскости, поэтому проанализируем, как связаны корни характеристического уравнения с видом F(j). Поскольку полином (4.16) можно представить как произведение простейших сомножителей

F(p) = (p - )(p - ), (4.19)

характеристический комплекс (4.17) также принимает вид:

F(j) = (4.20)

Его можно представить в форме

(4.21)

Из выражений (4.18) и (4.21) следует, что

(4.22)

(4.23)

Если характеристическое уравнение системы содержит чисто мнимые корни, то, как следует из (4.22), при определенном значении частоты , так как при этом один из сомножителей обратится в ноль. В случае устойчивой системы корни расположены только в левой полуплоскости плоскости корней и не могут быть чисто мнимыми, следовательно, в ноль годограф Михайлова не обращается.

Определим теперь угол поворота вектора при изменении частоты от 0 до . Поскольку , в соответствии с (4.23), есть сумма отдельных , то рассмотрим угол поворота каждого сомножителя выражения (4.20).

• 

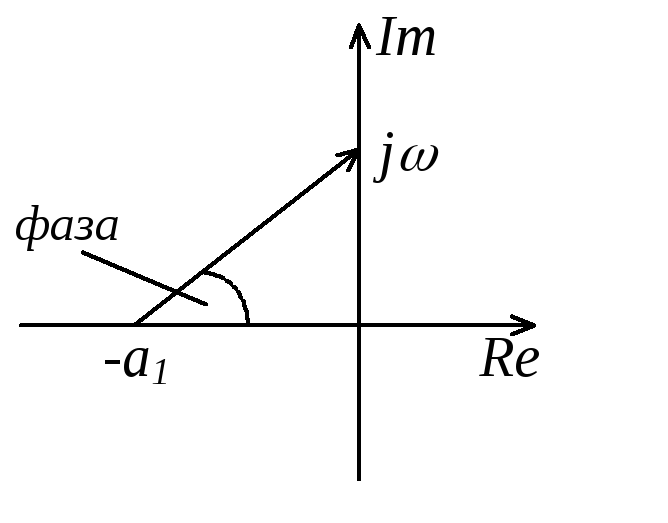
  1). Корень характеристического уравнения вещественный отрицательный; Соответствующий сомножитель в (4.20) имеет вид: (). Изобразим этот элементарный вектор на комплексной плоскости; при изменении от 0 до его вещественная часть остается неизменной и равна , а мнимая часть возрастает до бесконечности.

Как видим, угол поворота элементарного вектора, соответствующего устойчивому вещественному корню, равен

Рис. 4.9. Элементарный вектор, соответствующий

устойчивому вещественному корню

Если корень характеристического уравнения вещественный положительный, , то угол поворота элементарного вектора равен

• 2). Рассмотрим теперь пару устойчивых комплексно - cопряженных корней и соответствующий им угол поворота произведения

У этих двух векторов начальные фазы одинаковы по модулю (), но имеют противоположные знаки. При изменении от 0 до один вектор поворачивается на угол, равный , а второй - на угол

Суммарный угол поворота для пары устойчивых комплексно - сопряженных корней равен

Рис. 4.10. Векторы, соответствующие устойчивым

комплексно - сопряженным корням

Если комплексно - сопряженные корни имеют положительную вещественную часть, то суммарный угол поворота равен

Таким образом, в устойчивой системе каждый из n корней даст приращение фазы , а общий угол поворота согласно (4.23) равен , что и требовалось доказать. Вид годографа Михайлова для устойчивых и неустойчивых систем третьего порядка приведен на рис. 4.11.

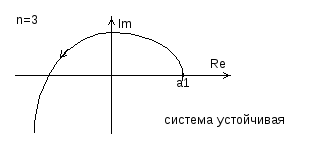
Рис. 4.11. Годограф Михайлова устойчивой и неустойчивой систем

Система будет находиться на границе устойчивости, если годограф Михайлова при некотором значении частоты обращается в ноль, то есть при выполнении условия:

(4.24)

Здесь частота ₀ - есть частота незатухающих колебаний системы.