Глава 5. Случайные величины и их распределения
§1. Понятие случайной величины
Определение. Случайной величиной ξ называется функция, ставящая в соответствие каждому элементарному исходу ω число ξ = ξ(ω).
Пример 1. Рассмотрим схему Бернулли с вероятностью успеха p . Сопоставим каждому элементарному исходу ω =10100...0 функцию ξ(ω), равную числу успехов данно-
го исхода, т.е. числу символов 1, содержащихся в последовательности 10100...0 . Пример 2. Случайными величинами является число очков при бросании игральной
кости, сумма очков при бросании нескольких игральных костей.
Пример 3. Случайной величиной является координата точки, упавшей на отрезок [0;1]. В этом случае ξ(ω)= ω .
В общем случае случайные величины делятся на дискретные и непрерывные. Определение. Дискретной называется случайная величина, которая каждому эле-
ментарному исходу ω ставит в соответствие одно из конечного (или в общем случае счетного) набора чисел x1 ,x2 ,...,xn (x1 ,x2 ,...,xn ,...).
Определение. Непрерывной называется случайная величина, возможные значения которой непрерывно заполняют некоторую область.
Однако существуют случайные величины, не относящиеся ни к одному из этих типов. Простейшим примером такой случайной величины является время работы электроприбора. Купленный электроприбор может с ненулевой вероятностью оказаться бракованным, т.е. время его работы будет равно 0, и в этом смысле необходимо считать рассматриваемую случайную величину дискретной. Если же прибор окажется исправным, то время его работы необходимо считать непрерывной случайной величиной.
§2. Функция распределения случайной величины
Определение. Функцией распределения (вероятностей) случайной величины ξ
называется функция F (x), значения которой в точке x равно вероятности события
(ξ < x):
F (x)= P(ξ < x). |
(5.2.1) |
Свойства функции распределения.
1. Функция распределения является ограниченной, т.е. 0 ≤ F(x)≤1.
Доказательство. Ограниченность функции распределения следует из того, что функция распределения является вероятностью.
2. Функция распределения является неубывающей, т.е. если x2 > x1 , то
F (x2 )≥ F(x1 ).
Доказательство. Если x2 > x1 , то событие (ξ < x1 ) содержится в событии (ξ < x2 ), т.е. (ξ < x1 ) (ξ < x2 ). Отсюда, по свойству 3 вероятности, имеем
P(ξ < x1 )≤ P(ξ < x2 ),
откуда, следует
F (x1 )≤ F(x2 ).
29
3. F(x) обращается в ноль на минус бесконечности, т.е.
F(−∞)= 0 .
Доказательство. Событие (ξ < −∞) является невозможным событием, следовательно, P(ξ < −∞)= 0 .
4. F(x) равна единице в плюс бесконечности, т.е.
F(+ ∞)=1.
Доказательство. Событие (ξ < +∞) является достоверным событием, следователь-
но, P(ξ < +∞)=1.
5. Вероятность попадания случайной величины ξ в интервал [x1 ,x2 ) равна прира-
щению ее функции распределения на этом промежутке, т.е.
P(x1 ≤ ξ <x2 )= F(x2 )− F(x1 ).
Доказательство. При x1 < x2 событие (ξ < x2 ) можно представить как объединение двух непересекающихся событий (ξ < x1 ) и (x1 ≤ ξ <x2 ). Отсюда, используя аксиому
сложения, получаем
P(ξ < x2 )= P(ξ < x1 )+ P(x1 ≤ ξ <x2 ), P(x1 ≤ ξ <x2 )= P(ξ < x2 )− P(ξ < x1 )
или, используя определение функции распределения, получаем
P(x1 ≤ ξ <x2 )= F(x2 )− F(x1 ). 6. F(x) непрерывна слева, т.е.
lim F(x)= F(x0 ).
x→x0 −0
С помощью функции распределения можно вычислить вероятность события
(ξ ≥ x):
P(ξ ≥ x)=1− F(x). |
(5.2.2) |
Иногда, чтобы подчеркнуть, кокой именно случайной величине принадлежит |
|
функция распределения F (x), |
к функции распределения приписывают нижний индекс, |
обозначающий эту случайную величину, т.е.
Fξ (x)= P(ξ < x).
Иногда функцией распределения называется вероятность события (ξ ≤ x). Такое определение ничего не меняет во всех рассуждениях. Единственное изменение касается свойства 6: функция F(x) будет непрерывной справа.
§3. Дискретные случайные величины
Как уже говорилось, дискретной называется случайная величина, которая каждому элементарному исходу ω ставит в соответствие одно из конечного (или в общем случае счетного) набора чисел x1 ,x2 ,...,xn (x1 ,x2 ,...,xn ,...).
Дискретную случайную величину удобно характеризовать рядом распределения.
Определение. Рядом распределения (вероятностей) дискретной случайной вели-
чины называется таблица (таблица 5.1), состоящая из двух строк: в первой строке перечислены все возможные значения случайной величины, а во второй — вероятности pi = P(ξ = xi ) того, что случайная величина ξ примет значение xi .
30
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
x1 |
x2 |
… |
|
xi |
|
… |
xn |
|
… |
|
|
P |
|
p1 |
p2 |
… |
|
pi |
|
… |
pn |
|
… |
|
При этом должно выполняться равенство |
|
|
|
|
|
|
|
||||||
|
∑pi |
=1. |
|
|
|
|
|
|
|
|
(5.3.1) |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
Функцию распределения дискретной случайной величины можно определить по |
|||||||||||||
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (x)= ∑pi . |
|
|
|
|
|
|
|
(5.3.2) |
|
|||
|
|
xi <x |
|
|
|
|
|
|
|
|
|
|
|
Пример 4. Производится один опыт, в результате которого может произойти собы- |
|||||||||||||
тие A с вероятностью p . Рассмотрим случайную величину |
|
|
|
|
|
||||||||
ξ = 1, еслисобытиеA произошло, |
|||||
|
0, еслисобытиеA непроизошло. |
||||
Для случайной величины ξ ряд распределения и найти ее функцию распределения. |
|||||
Решение. Очевидно, что ряд распределения имеет вид: |
|||||
|
|
|
|
|
|
|
ξ |
|
0 |
1 |
|
где q |
P |
|
q |
p |
|
=1− p . |
|
|
|
||
Функцию распределения случайной величины ξ найдем по формуле (5.3.2). |
|||||
Пусть |
x ≤ 0 . В этом случае событие (ξ < x) является невозможным, так как слу- |
||||
чайная величина ξ не принимает значений меньших 0. Отсюда получаем:
F (x)= ∑pi = 0 .
xi <x
Пусть 0 < x ≤1. В этом случае событие (ξ < x) совпадает с событием (ξ = 0), следовательно:
F (x)= ∑pi = P(ξ = 0)= q .
xi <x
Пусть x >1. В этом случае событие (ξ < x) является достоверным, следовательно
F (x)= ∑pi = P(ξ = 0)+ P(ξ =1)= q + p =1.
xi <x
Таким образом, функция распределения примет вид:0, если x ≤ 0;
F (x)= 1− p, если0 < x ≤1;
1, если x >1.
z
Пример 5. Рассмотрим схему последовательных независимых испытаний, в каждом из которых с вероятностью p может произойти событие A . Рассмотрим случайную
величину ξ — число испытаний, которое необходимо произвести, прежде чем событие A произойдет. Построить ряд распределения случайной величины ξ .
Решение. Случайная величина ξ может принимать значения 0, 1 ,...,n,.... Случайная величина ξ принимает значение 0, если в первом же испытании произойдет собы-
тие A , следовательно:
P(ξ = 0)= p .
31
Случайная величина ξ принимает значение 1, если в первом испытании событие A
не произошло, а во втором испытании событие A произойдет, следовательно,
P(ξ =1)= qp .
Случайная величина ξ принимает значение 2, если в первых двух испытаниях со-
бытие A не произошло, а в третьем испытании событие A произойдет, следовательно, |
||||||||||
|
P(ξ = 2)= qqp = q2 p . |
|
|
|
|
|
|
|||
Продолжая аналогично данные рассуждения, получим ряд распределения: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
0 |
|
1 |
2 |
… |
n |
… |
|
|
P |
|
p |
|
qp |
q2 p |
… |
qn p |
… |
|
|
|
|
|
|
|
|
|
|
|
z |
Пример 6. На зачете студент получил n = 4 задачи. Вероятность решить правиль- |
||||||||||
но каждую задачу |
p = 0,8 . Построить ряд распределения случайной величины ξ — числа |
|||||||||
правильно решенных задач.
Решение. Случайная величина ξ может принимать значения 0, 1, 2, 3, 4. Для нахождения вероятности событий (ξ = k ) (k = 0,1,2,3,4) применим формулу Бернулли:
P(ξ = 0)= p4 (0)= C40 p0 (1− p)4 = (1−0,8)4 = 0,0016 ,
P(ξ =1)= p4 (1)= C41 p1 (1− p)3 = 3!1!4! (0,8)1 (1−0,8)3 = 0,0256 , P(ξ = 2)= p4 (2)= C42 p2 (1− p)2 = 2!2!4! (0,8)2 (1−0,8)2 = 0,1536 , P(ξ = 3)= p4 (3)= C43 p3 (1− p)1 = 1!3!4! (0,8)3 (1−0,8)1 = 0,4096 ,
P(ξ = 4)= p4 (4)= C44 p4 (1− p)0 = 0,84 = 0,4096 .
Таким образом, ряд распределения числа правильно решенных задач примет вид:
ξ |
0 |
1 |
2 |
3 |
4 |
P |
0,0016 |
0,0256 |
0,1536 |
0,4096 |
0,4096 |
z
§4. Непрерывные случайные величины
Как уже говорилось, непрерывной называется случайная величина, возможные значения которой непрерывно заполняют какую-то область. Дадим более строгое определение непрерывной случайной величины.
Определение. Случайная величина ξ |
называется непрерывной, если ее функцию |
|
распределения F (x) можно представить в виде: |
||
F (x)= ∫x |
p(y)dy . |
(5.4.1) |
−∞ |
|
|
Определение. Функция p(x), присутствующая в (5.4.1), называется плотностью распределения (вероятностей) случайной величины ξ .
Отметим, что все реально встречающиеся плотности распределения являются непрерывными (за исключением, быть может, конечного числа точек) функциями, и, следо-
32
вательно, для них плотность распределения |
p(x) представляет собой производную функ- |
ции распределения F (x), т. е. |
|
′ |
(5.4.2) |
p( x ) = F ( x ) . |
Свойства плотности распределения:
1. Плотность является неотрицательной функцией, т.е. p(x) ≥ 0 .
Доказательство. Функция распределения — неубывающая функция. Следовательно, ее производная, которая по (5.4.2.) является плотностью, есть неотрицательная функция.
2. Вероятность попадания случайной величины ξ в интервал [x1 ,x2 ) равна определенному интегралу от ее плотности в пределах от x1 до x2 , т.е.
x2
P(x1 ≤ ξ < x2 )= ∫ p(y)dy .
x1
Доказательство. С одной стороны, по свойству 5 функции распределения
P(x1 ≤ ξ < x2 )= F(x2 )− F (x1 ), c другой стороны, в силу (5.4.2):
x∫2 p(y)dy = x∫2 dF(x)= F(x)x2 = F(x2 )− F(x1 ).
x1
x1 |
x1 |
3. Условие нормировки: несобственный интеграл от плотности случайной величины в бесконечных пределах равен единице, т.е.
+∞∫p(x)dx =1 .
−∞
Доказательство. В силу свойства 2, имеем
+∞∫ p(x)dx = F(+∞) − F (−∞) =1.
−∞
4. P(x ≤ ξ < x + x)≈ p(x) x .
Доказательство. Из свойства 2 следует, что вероятность попадания случайной величины на интервал [x1 , x2 ) численно равна площади криволинейной трапеции (рис. 5.1).
Как видно из рис. 5.1, при x → 0 вероятность попадания на интервал [x, x + x) приближенно совпадает с площадью прямоугольника со сторонами x и p(x).
33
5. Для непрерывных случайных величин Ρ(ξ = x)= 0 . Доказательство. Достаточно применить свойство 4, где x = 0 .
6. Для непрерывных случайных величин свойство 2 можно переписать в виде:
Ρ(x1 ≤ ξ < x2 ) = Ρ(x1 < ξ < x2 ) = Ρ(x1 < ξ ≤ x2 ) = Ρ(x1 ≤ ξ ≤ x2 ) .
Пример 7. Случайная величина ξ имеет плотность
0, |
x ≤ a ; |
|
|
|
|
p(x)= |
1 |
, a < x ≤ b ; |
|
||
b − a |
x > b. |
|
0, |
||
График функции p(x)изображен на рис. 5.2.
Найти функцию распределения F(x) случайной величины ξ и изобразить ее гра-
фик.
Решение. Для решения задачи применим формулу (5.4.1). При x ≤ a получаем, что
F(x)= ∫x |
p(t)dt = ∫x 0dt = 0 . |
|
|
|
|
|
|
|
||||||
−∞ |
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
При a < x ≤ b получаем: |
|
|
|
|
|
|
|
|||||||
F (x)= ∫x |
p(t)dt = ∫0 |
p(t)dt + ∫x |
p(t)dt = ∫0 0dt + ∫x |
1 |
dt = |
x − a |
. |
|||||||
|
|
|||||||||||||
−∞ |
|
|
|
−∞ |
|
|
0 |
|
−∞ |
a b − a |
|
b − a |
||
При x > b имеем: |
|
|
|
|
|
|
|
|
|
|
||||
F( x ) = ∫x |
p( t )dt = ∫a |
p( t )dt + ∫b |
p( t )dt + ∫x |
p( t )dt =1. |
||||||||||
−∞ |
|
|
−∞ |
|
|
a |
b |
|
|
|
|
|
||
Таким образом, получаем |
|
|
|
|
|
|
|
|||||||
0, |
|
x ≤ 0, |
|
|
|
|
|
|
|
|
||||
|
|
|
− a |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||
F( x ) = |
|
|
|
, a < x |
≤ b, |
|
|
|
|
|
|
|
||
|
|
− a |
|
|
|
|
|
|
|
|||||
b |
x > b. |
|
|
|
|
|
|
|
|
|||||
1, |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34
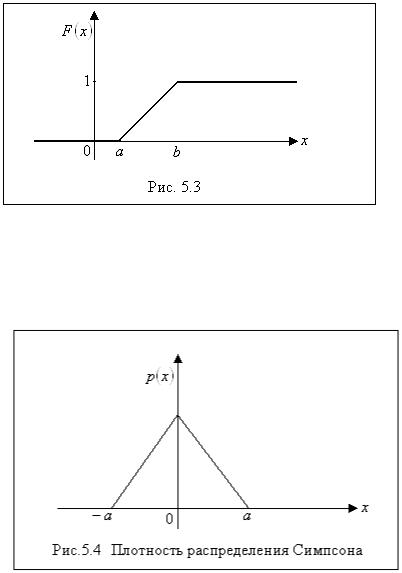
График функции распределения изображен на рис. 5.3. z
Пример 8. Случайная величина ξ подчинена закону Симпсона («закону равнобедренного треугольника») на участке [− a, a] (рис. 5.4).
Найти плотность распределения и функцию распределения.
Решение. Используя свойство 3 плотности, найдем высоту треугольника:
1 = +∞∫p(x)dx = |
1 |
h 2a = ah h = |
1 |
. |
|||||||||||
|
|
|
|
|
|
|
|||||||||
−∞ |
|
|
|
2 |
|
|
a |
||||||||
Далее находим уравнения ребер: |
|||||||||||||||
p(x)= |
1 |
|
− |
|
x |
x [0,a]; |
|
|
|||||||
|
1 |
|
|
|
|
|
, при |
|
|
||||||
a |
|
|
|
|
|
||||||||||
|
|
|
a |
|
|
|
|||||||||
p(x)= |
1 |
|
+ |
|
x |
x [−a,0] |
|
|
|||||||
|
1 |
|
|
|
|
|
, при |
|
|
||||||
a |
|
|
|
|
|
|
|||||||||
или |
|
|
a |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||||
p(x)= |
1 |
− |
|
|
|
|
|
|
|
, при x [− a,a]. |
|||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||
|
a |
|
|
a |
|
|
|
||||||||
Найдем функцию распределения F( x ) .
Очевидно, что при x ≤ −a функция распределения равна нулю, т.е. F(x) = 0 . Далее, при − a < x ≤ 0 :
x |
−a |
x |
x |
1 |
|
|
t |
1 |
|
x |
2 |
|
|
1 |
|
|
F (x) = ∫p(t)dt = ∫p(t)dt + ∫p(t)dt = ∫ |
|
|
|
|
|
|
||||||||||
|
1 |
+ |
|
dt = |
|
|
|
+ |
|
. |
||||||
|
|
|
x + |
|
|
|
|
|||||||||
−∞ |
−∞ |
−a |
−a a |
|
|
a |
a |
|
2a |
|
2 |
|
||||
|
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|