Анализ остатков и прогноз
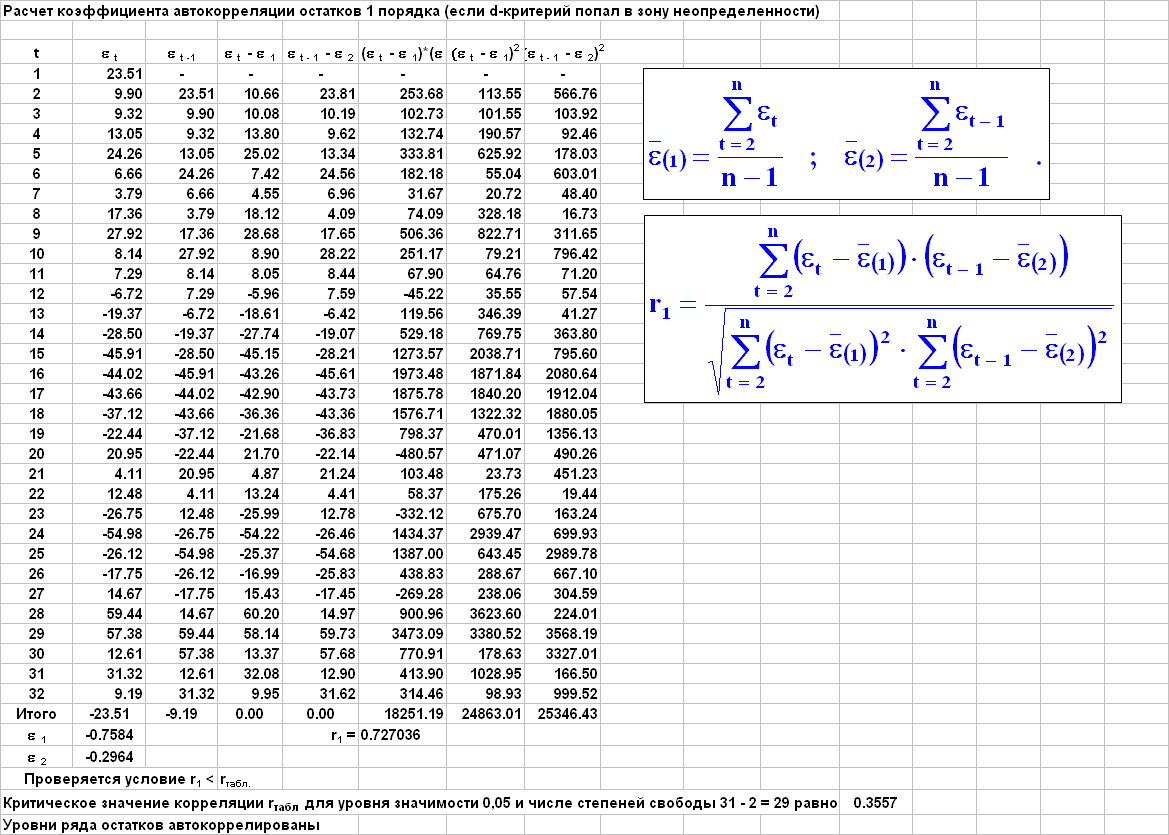
Тесты Колмогорова-Смирнова для проверки гипотезы о нормальном распределении остатков.
Результаты анализа остатков для различных моделей:
Для линейной, экспоненциальной и регрессионной моделей не соблюдаются предпосылки МНК, они могут использоваться лишь для предварительного прогноза анализируемого показателя. Модель Брауна характеризуется хорошей точностью и может применяться для краткосрочного прогноза динамики средней цены анализируемой литературы, если есть основания ориентироваться на последние наблюдения..
Прогноз по линейной модели
Прогноз по экспоненциальной модели
Прогноз строится для линеаризованной модели (для Ln(y)), затем пересчитывается на исходные значения y.
Прогноз по модели Брауна
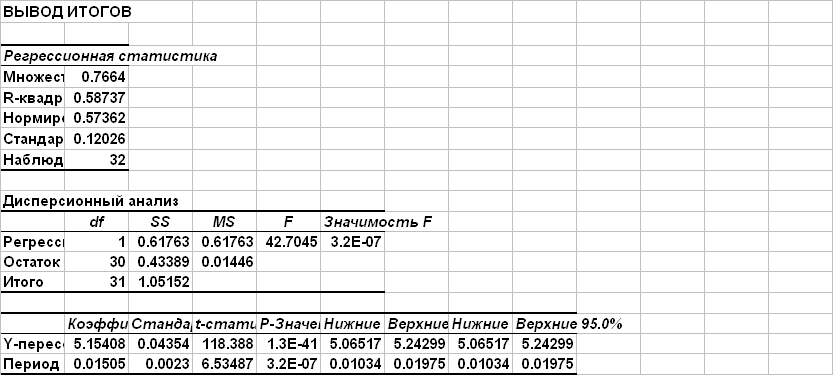
Прогноз по регрессионной модели
Для расчета прогнозных значений уровня цен используется линейный тренд
Далее прогнозные значения уровня цен используются для расчета точечного прогноза средних цен книг по разделу Компьютерная литература.
Модели arima
Построение наиболее популярных моделей ARIMA
p=0, d=1, q=1
Модель содержит незначимый параметр q(1), поэтому далее не рассматривается.
p=0, d=2, q=1
Модель ARIMA(0, 2, 1) не содержит незначимых параметров. Стандартная ошибка прогноза на 1 шаг для модели ARIMA(0, 2, 1) равна 23.20 против 30.97 для линейной модели. При увеличении горизонта прогноза преимущество имеет линейная модель. Стандартная ошибка прогноза на 5 шагов для модели ARIMA(0, 2, 1) равна 61.27 против 31.70 для линейной модели.:
p=0, d=1, q=2
Модель ARIMA(0, 1, 2) содержит незначимые параметры q(1) и q(2), поэтому далее не рассматривается..
p=0, d=2, q=2
Модель ARIMA(0, 2, 2) содержит незначимый параметр q(2) и далее не рассматривается.
p=1, d=1, q=0
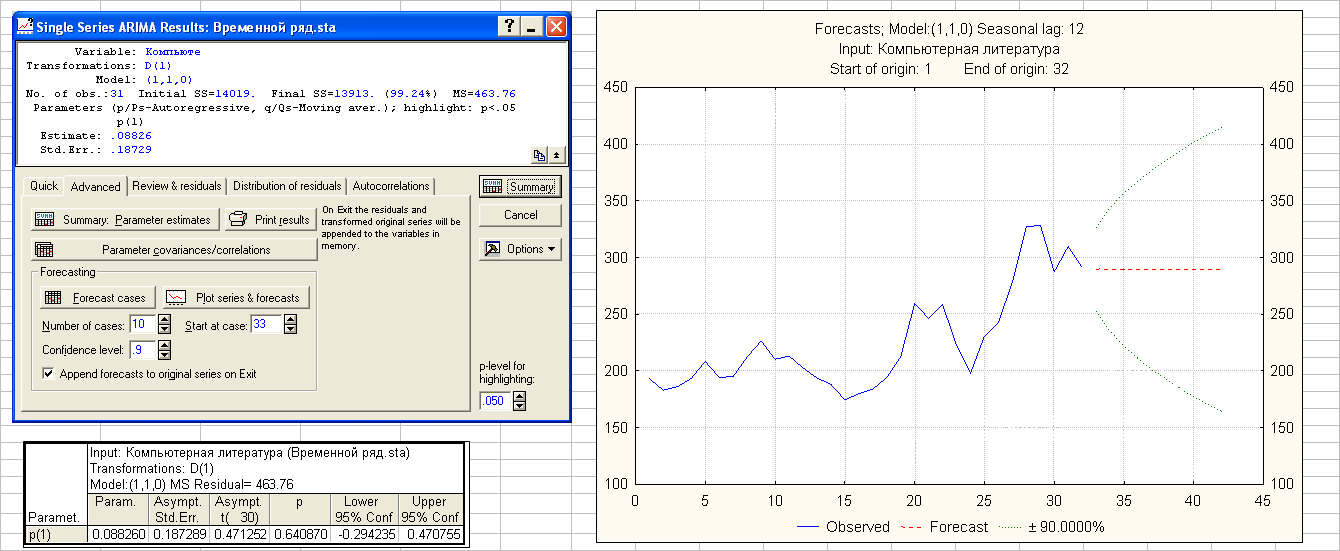
Модель ARIMA(1, 1, 0) содержит незначимый параметр p(1) и далее не рассматривается.
p=2, d=1, q=0
Модель ARIMA(2, 1, 0) содержит незначимые параметры p(1) и p(2), поэтому далее не рассматривается.
p=1, d=2, q=0
По точности прогноза модель ARIMA (1, 2, 0) уступает модели ARIMA (0, 2, 1). Стандартная ошибка прогноза на 1 шаг равна 26.50 против 23.20 для модели ARIMA (0, 2, 1) и резко возрастает с увеличением горизонта прогноза.
p=1, d=1, q=1
Модель ARIMA (1, 1, 1) не содержит незначимых параметров. По точности прогноза она превосходит все рассмотренные ранее модели ARIMA. Стандартная ошибка прогноза на 1 шаг равна 21.36 против 23.20 для модели ARIMA (0, 2, 1) и 30.97 - для линейной модели.
p=1, d=1, q=1
Модель ARIMA (1, 2, 1) содержит незначимый параметр p(1) и далее не рассматривается..
Вывод:
По точности кратковременного прогноза (на 1 - 2 шага) полученные модели ARIMA конкурентноспособны по сравнению с линейной и другими рассмотренными ранее моделями временных рядов. Их целесообразно использовать, когда есть основания считать более значимыми последние наблюдения временного ряда. Из 9 рассмотренных моделей ARIMA лучшей является модель ARIMA (1, 1, 1). Она не содержат незначимых параметров, ей соответствует наименьшее по сравнению с другими рассмотренными моделями значение стандартной ошибки прогноза 1-го шага: 21.36 против 23.20 для модели ARIMA (0, 2, 1) и 30.97 - для линейной модели.