Как написать программу на QuickВаsic, соответствующую этому методу?

Прежде всего, функцию, корень которой мы ищем, лучше всего описать в виде отдельной function. Во время выполнения программа должна запросить начальные значения а и b.

Далее нужно проверить, что f(а) и f(b) действительно разных знаков. Это условие можно записать двумя разными способами:

1. ((f (а) <= 0) and (f (b) > 0)) or ((f (b) <= 0) and (f (a) > 0))

2. f (a) * f(b) <= 0

Если это не так, нужно только напечатать сообщение об ошибке, иначе можно приступать к поиску корня. Поиск проще всего оформить в виде цикла:

Do until (b-а) < eps ... loop

Здесь eps - константа, равная, например 10ˉ⁵. На каждой итерации цикла нужно вычислить значение точки с и сравнить знак функции в этой точке со знаком f(а). Если знаки разные, о точке b можно "забыть": b:=с. Иначе – "забываем" о точке а. После окончания цикла остается лишь напечатать найденный корень. Ближе всего к корню будет, скорее всего, середина окончательного отрезка [а,d],

длина которого не превышает заданной точности eps.

2). Метод касательных.

Метод Ньютона, или метод касательных основан на вычислении не только значений функции, но и значений ее производной. Разложим f(х) в ряд Тейлора и отбросим члены ряда выше второго порядка:

f (х) = f (х0) + f’ (х0)(х – x0)

В этом приближении корень функции легко найти по формуле:

f (x) = 0, при xi = xi+1 – f (x0)/f ' (x0)

Для нелинейных функций это, конечно, не точное равенство, но способ получить значение, более близкое к корню. Таким образом, метод Ньютона состоит в построении последовательности итераций:

x1 = x0 – f (x0)/ f ' (x0)

x2 = x1 – f (x1)/ f ' (x1)

xi+1 = xi – f (xi)/ f ' (xi)

На какой итерации завершать процесс нахождения корня? Возможно два варианта: либо когда значение функции станет достаточно маленьким по абсолютной величине:

| f (x)| < eps, либо когда практически перестанет меняться значение х:

| f (x)/ f '(x)| < eps

| Xi+1 – Xi| <= eps

3). Метод простой итерации

Рассматриваемый метод реализует третий подход к решению задачи. Предварительно исходное уравнение f(х) = 0 преобразуют к виду φ(х)=х, что является частным случа­ем более общей структуры g(х)=f(x).Затем выбирают началь­ное значение х0 и подставляют его в левую часть уравнения, но φ(x)≠ х0, поскольку x₀ взято произвольно и не является корнем уравнения.

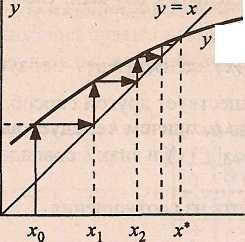
Полученное φ(x)=x1 рассматривают как очередное приближение к корню. Его снова подставляют в левую часть уравнения φ(х1) и получают следующее значение х2 (х2 = φ(x1) и т.д., в общем случае хi+1 =φ(хi). Получающаяся таким образом последовательность х0,x1, х2, х3, х4,… при определенных услови­ях может сходиться к корню х* (рис. 1.a).

Таким условием является |φ’(x)| <= 1 на [а,b], причем чем ближе модуль к нулю, тем выше окажется скорость сходимости к решению. В про­тивном случае последовательность расходится от искомого решения (“метод не сходится”).

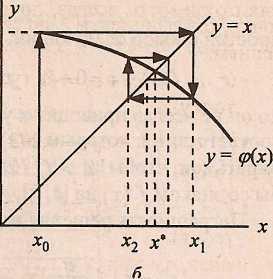
На рисунке 2 приведён один из возможных случаев, когда итерационный

процесс не сходится. Видно, что последовательность х0,x1, х2,… удаляется от

корня х*. Это всегда будет иметь место в том случае, если тангенс угла наклона φ(x) в окрестности корня по модулю больше единицы.

Существуют различные способы преобразования уравнения f(x) = 0 к виду φ(x) = x; одни могут привести к выполнению условия сходимости всегда, другие – в отдельных случаях.

Самый простой способ следующий:

f(x) + x = 0 + x, f(x) + x = φ(x) => φ(x) = x,

(а)	(б)	(в)
	Pис.6

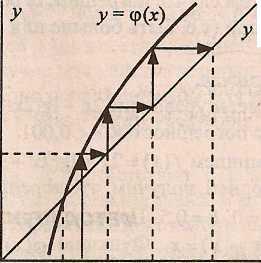
а) 0 < φ’(х) < 1;б) – 1 < φ’(х) < 0

но он не всегда приводит к успеху. Существует другой способ, в соответствии с которым φ(х)=х-f(х)/к, причем k следует вы­бирать так, чтобы

|k| >Q/2, где Q=mах |f'(х)| и знак к совпадал бы со знаком f'(х) на [а, b].

Погрешность решения можно оценить из соотношения

|x* - xi| <= (q/(1 – q))*|X(i) – X(i+1)|, где q = max φ(х).

Вследствие этого для окончания вычислений в методе итера­ций применят соотношение (q/(q – 1))*|X(i) – X(i + 1)|<= ε , где ε — заданная погрешность решения. Часто используют упрощенное условие окончания поиска |X(i) – X(i + 1)|<=ε не вычисляя максимальное значение производной, но в этом случае погрешность решения может не соответствовать заданной (т.е. быть больше или меньше).