Статистическое заключение

По результатам регрессионного анализа можно сделать заключение, что линейное уравнение с логарифмированием факторного признака, представленное результатами опыта у = -14,69 + 11,42×ln x_i в 55,53 раза лучше описывает изменение зависимой переменной чем среднее значение аргумента.

7.2. Уравнение гиперболы

Для вычисления коэффициентов a и b гиперболической зависимости:

необходимо решить следующую систему уравнений:

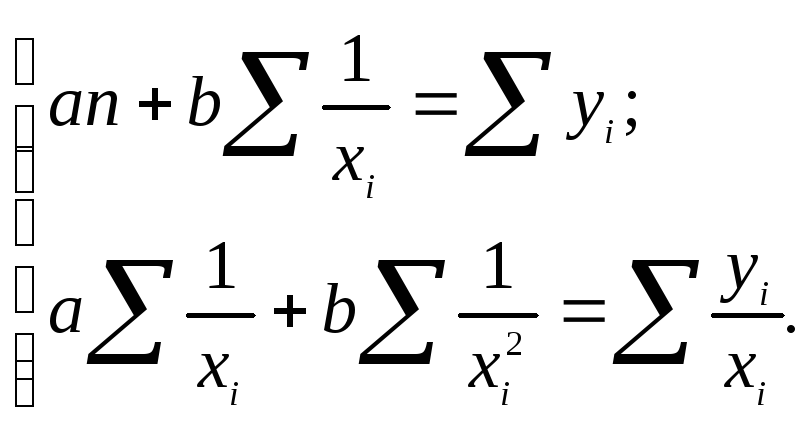
Результатом решения системы нормальных уравнений являются следующие выражения:

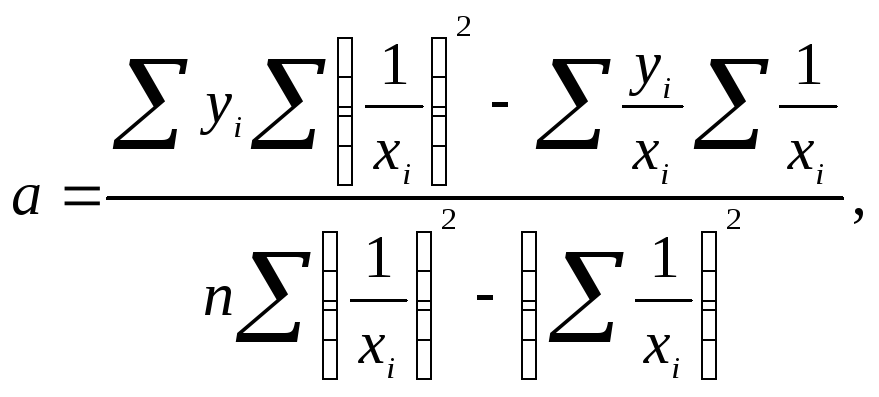
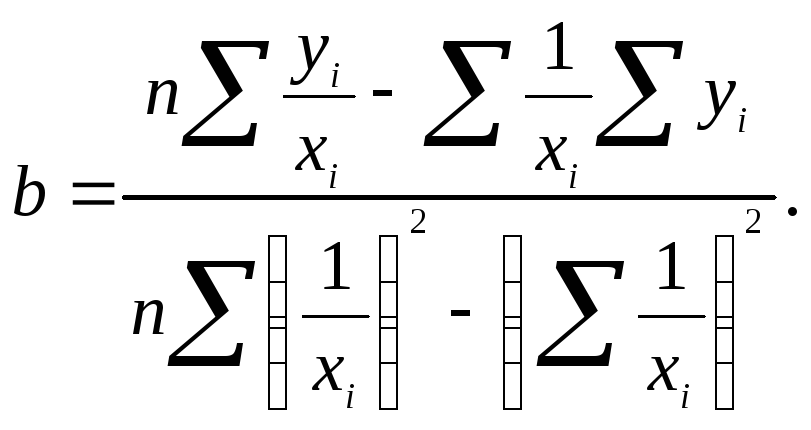
Расчет вспомогательных величин для нахождения коэффициентов уравнения приведен в таблице 1.8.2.

Таблица 7.2 Расчет вспомогательных величин для нахождения коэффициентов a и b

Диаметр, xi, см	Высота, yi, м	yi2	1/xi	(1/xi)2	yi/xi	yx=30,965-197/xi	yi-yx	(yi-yx)2
1	2	3	4	5	6	7	8	9
8	9,5	90,25	0,13	0,02	1,19	6,34	3,16	9,98
12	13,4	179,56	0,08	0,01	1,12	14,54	-1,15	1,32
16	16,3	265,69	0,06	0,01	1,02	18,65	-2,35	5,53
и т.д.
360	264,2	6293,90	0,54	0,04	9,85	сумма	-0,01	53,05

Полученное уравнение регрессии имеет вид y_х = 30,965 – (197 / x_i).

Дальнейшие расчёты производятся по аналогии с пунктом 7.1. Представить графически изменение высот от диаметров (смотри уравнение гиперболы).

Статистическое заключение

По результатам регрессионного анализа можно сделать заключение, что уравнение гиперболы, представленное результатами опыта вид y_х = 30,965 – (197 / x_i) в 8,18 раза лучше описывает изменение зависимой переменной чем среднее значение аргумента.

7.3. Уравнение показательной кривой

Для вычисления коэффициентов а и в для уравнения

необходимо решить следующую систему нормальных уравнений:

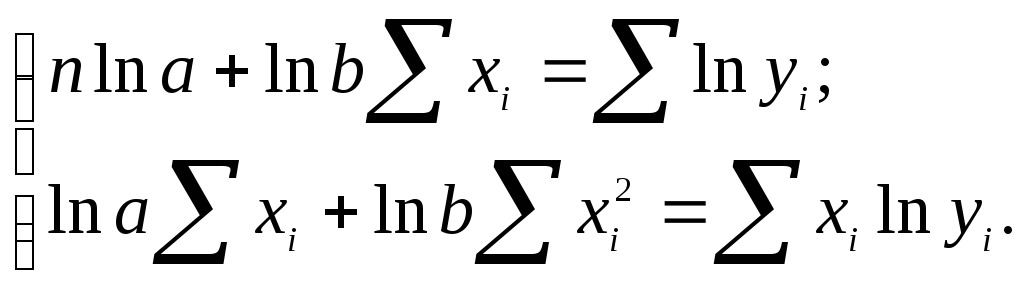
Решение системы относительно неизвестных а и в дает численные значения искомых коэффициентов:

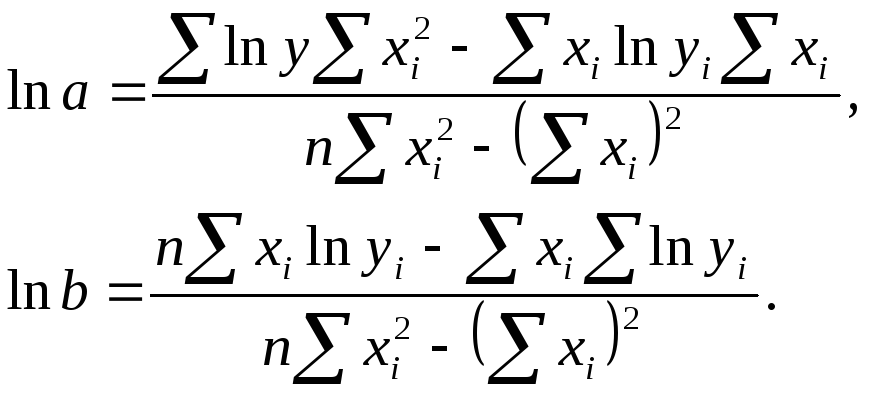
Пример: Найти уравнение регрессии, описывающее фактические значения высот по диаметрам в сосновом древостое, используя уравнение показательной кривой.

Расчет вспомогательных величин для нахождения коэффициентов уравнения приведен в таблице 7.3

Таблица 7.3 Расчет вспомогательных величин для нахождения коэффициентов а и в

Диаметр, хi,см	Высота, уi,м	xi2	yi2	lnyi,м	xilnyi	yx=10,35× ×1,024x	yi-yx	(yi-yx)2
1	2	3	4	5	6	7	8	9
8	9,5	64	90,25	2,25	18,01	12,51	-3,01	9,06
12	13,4	144	179,60	2,59	31,14	13,76	-0,36	0,13
16	16,3	256	265,70	2,79	44,66	15,13	1,17	0,37
и т.д.
360	264	13088,00	6294,00	36,59	1152,00	сумма	-2,81	69,97

Полученное уравнение регрессии имеет вид у=10,35×(1,024^х_i).

Дальнейшие расчёты производятся по аналогии с пунктом 7.1.

Представить графически изменение высот от диаметров (смотри линейное уравнение с логарифмированием факторного признака).