Статистическое заключение

Работа по определению запаса глазомерным способом на пробных площадях, вторым таксатором выполнена более точно, так как его ошибка для всех случаев меньше, по сравнению с первым таксатором.

7.0 Регрессионный анализ Постановка задачи

Математические выражения, отражающие причинно-следственные взаимосвязи и взаимодействия в системах (или модели связи) являются основными типами моделей, применяемых в области лесного дела. В качестве математической формы эмпирических моделей связи, в основном, используют регрессионные уравнения и реже – интерполяционные многочлены. В первом случае применяют различные модификации метода наименьших квадратов, позволяющие просто и достаточно надежно оценить статистическим путем разрабатываемую модель. Второй метод сводится к механической процедуре аналитического выражения числовых массивов.

Для вычисления коэффициентов регрессионных уравнений основным методом является метод наименьших квадратов, предложенный в начале XIX в. Лежандром и Гауссом. Требование метода наименьших квадратов заключается в том, что теоретические точки линии регрессии y должны быть получены таким образом, чтобы сумма квадратов отклонений от этих точек эмпирических значений была минимальной, то есть

7.1. Линейное уравнение с логарифмированием факторного признака

Для вычисления коэффициентов a и b для уравнения прямой с логарифмированием факторного признака

необходимо решить следующую систему уравнений:

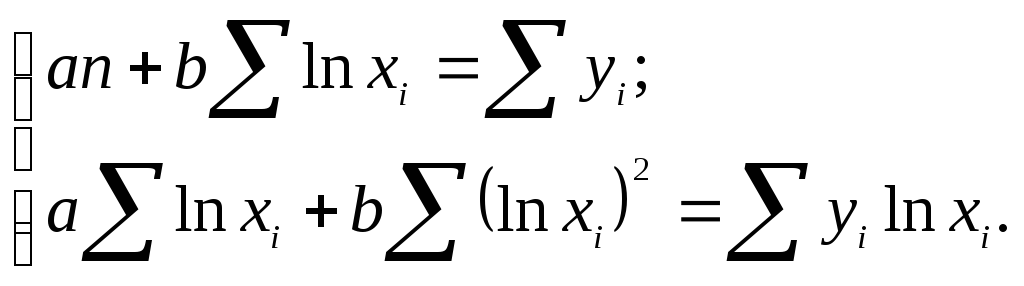
Решение системы относительно неизвестных a и b дает численные значения искомых коэффициентов:

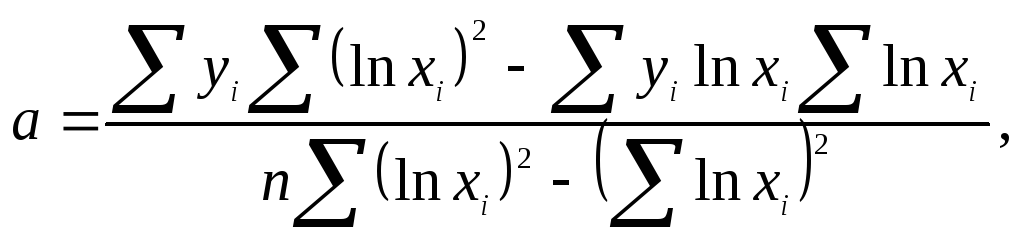
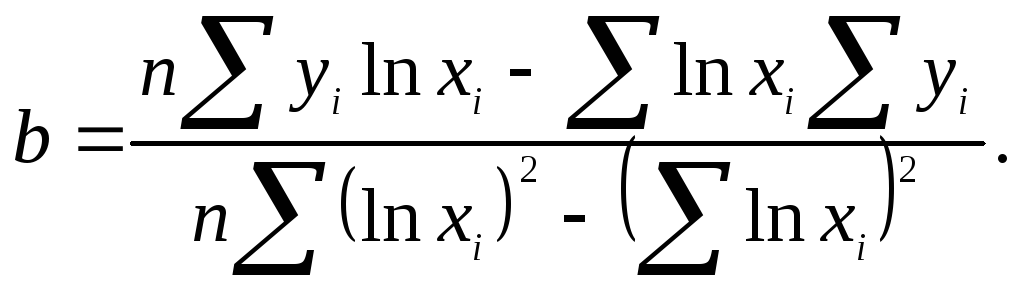
Пример: Найти уравнение регрессии, описывающее фактические значения высот по диаметрам в сосновом древостое, используя линейную модель с логарифмированием факторного признака.

Расчет вспомогательных величин для нахождения коэффициентов уравнения приведен в таблице 7.1.

Таблица 7.1 Расчет вспомогательных величин для нахождения коэффициентов a и b

Диаметр, xi , см	Высота, yi ,м	yi2	ln xi	(ln xi )2	yi×lnxi	yx = –14,69 + 11,42×ln xi	yi – yx	(yi –yx)2
1	2	3	4	5	6	7	8	9
8	9,5	90,25	2,08	4,32	19,75	9,04	0,46	0,21
12	13,4	179,56	2,48	6,17	33,3	13,66	- 0,26	0,07
16	16,3	265,69	2,77	7,69	45,19	16,95	- 0,65	0,42
и т.д.
360,0	264,2	6293,90	39,19	131,74	905,02	сумма	-6,65	7,81

Найдя вспомогательные величины по таблице 7.1 подставляем их в исходные выражения или в формулы определения коэффициентов а и в.

По приведённому примеру коэффициенты а и в соответственно равны:

Полученное уравнение регрессии имеет вид y_х = -14,69 + 11,42×ln x_i.

Далее в 7 колонке таблицы 7.1 вычисляются высоты деревьев по полученному уравнению: например y_x = –14,69 + 11,42×2,08 = 9,04 и так далее.

В 8 и 9 колонках находят расхождение между высотой опытной (колонка 2) и высотой полученной по уравнению (колонка 7) и квадрат этого отклонения.

Проверка значимости уравнения регрессии производим по F – критерию Фишера, который равен отношению общеё дисперсии к дисперсии остаточной.

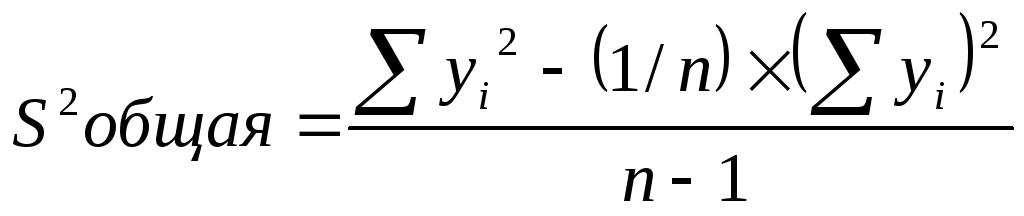
Например:

При сравнении фактического значения F – критерия с F – критерием стандартным на 5 или 1 % уровне значимости делаем заключение об адекватности модели. Если F_ф > F_st, то предложенная модель (уравнение) адекватно предсказывает изменение высот по диаметрам.

F_st берётся из приложения учебника, в зависимости от числа степеней свободы общей дисперсии (большая), и числа степеней свободы остаточной дисперсии (меньшая).

Число степеней свободы для общей дисперсии k₁=n-2

Число степеней свободы для остаточной дисперсии k₂=n-1

Для приведённого примера: k₁=n-2=12-2=10 k₂=n-1=12-1=11

F_st для 5 % уровня значимости равно 2,86.

Так как F_ф > F_st, то предложенная модель (уравнение) адекватно предсказывает изменение высот по диаметрам.

Представить графически изменение высот от диаметров для оценки адекватности модели по полученному уравнению. Построение графиков по исходным данным пунктирной линией (x_i ,y_i), по расчетным данным сплошной линией (x_i , y_x).