Статистическое заключение

При сравнительной оценке двух эмпирических рядов распределения деревьев сосны по диаметру на высоте груди, можно сделать вывод, что между ними имеются существенные различия, так как фактическое значение критерия λ_ф – Колмогорова – Смирнова больше теоретического на всех уровнях значимости.

3.4. Статистическое сравнение двух выборочных средних

по t – критерию Стьюдента при равнозначных выборках

Критерий t-Стьюдента используется для оценки достоверности различий средних значений выборочных совокупностей. Фактическое значение критерия определяют по формуле:

t = ,

где

d – разность между сравниваемыми средними

S_d – ошибка разности средних

и _– значение сравниваемых средних выборочных совокупностей

m_x1² и m_x2²- значение ошибок средних выборочных совокупностей.

Данная формула применяется для сравнения средних выборочных совокупностей с равнозначным объёмом; то есть n₁= n_2, где n₁и n_{2 –} объем сравниваемых выборочных совокупностей.

Пример расчёта t-критерия фактического приведён в таблице 3.4.

Таблица 3.4 Статистическое сравнение двух выборочных средних по t- критерию Стьюдента

Фамилия	Объём выборки n, шт	Средняя величина x, мм	Ошибка средней mx, мм	tфакт	t05/01
Иванов	30	31,08	0,85	12,43	2,05/2,76
Смирнов	30	47,30	0,99

t_{факт =}

Фактическое значения t- критерия (t_ф) сравнивается с t_St на1% и 5%-ном уровне значимости, которые определяются с использованием приложения учебника (Герасимов, Хлюстов). Причём число степеней свободы устанавливается по формуле: k=n – 1.

Для приведенного примера k=30 – 1=29, следовательно, t _{05/ 01} = 2,05/2,76.

Так как t_ф (8,84) больше t₀₁, Н₀- гипотеза отвергается, различия между средними существенные.

В курсовой работе произвести сравнительную оценку со средними пятерых студентов (все данные представить в виде одной таблицы).

Статистическое заключение

В результате сравнения выборочной средней Иванова со средней Смирнова делаем заключение о существенности различий между ними, т.к фактическое значении t критерия больше t на 1 % уровне значимости.

(в курсовой работе отметить с кем выявлены существенные, а с кем несущественные различия)

3.5. Статистическое сравнение двух выборочных средних

по t –критерию Стьюдента при неравнозначных выборках

Если объёмы выборочных совокупностей неравны (выборки неравнозначные), то критерий t- Стьюдента определяется по формуле:

t_ф=,

где S_d =,

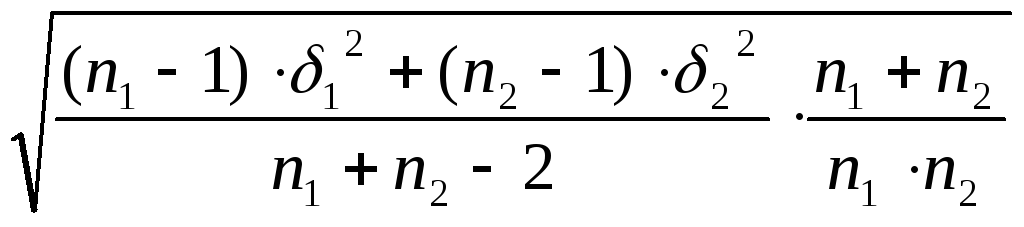d – разность между сравниваемыми средними

S_d – ошибка разности средних

и _– значение сравниваемых средних выборочных совокупностей

n₁ и n₂ –объёмы сравниваемых выборочных совокупностей;

и - значение стандартного отклонения.

Пример расчета вспомогательных величин для вычисления t- критерия фактического приведен в таблице 3.5

Таблица 3.5 Статистическое сравнение двух выборочных средних по t- критерию Стьюдента

Фамилия	Объём выборки n, шт.	Средняя величина , cм.	Стандартное отклонение σ,cм.	t факт	t 05/01
Иванов	100	24,88	7,45	6,23	1,96/2,58
Смирнов	552	22,02	4,08

S_d=

t_ф=.

Фактическое значение t- критерия (t _Ф) сравнивается с t_St на1% и 5%-ном уровне значимости.

t _{05/ 01} определяем по приложению учебника, исходя из числа степеней свободы.

Формула для вычисления числа степеней свободы имеет вид: k = n₁ + n₂ – 2.

Для приведенного примера k = 542 + 552 - 2 = 1092, следовательно, t_{05/ 01} = 1,96/2,58.

Так как t_факт(6,23) больше t₀₁ , Н₀-гипотеза отвергается, следовательно, различия существенные.