3. Критерии оценки статистических гипотез
Понятие статистической гипотезы предполагает проведение статистической оценки в подтверждение или отклонение рассматриваемого предположения. Статистические гипотезы подразделяют на виды:
- параметрические (требуется вычисление параметров распределения);
- непараметрические (не требуется вычисления параметров распределения).
На основании статистической оценки решается вопрос: принять или отвергнуть гипотезу. Для решения этого вопроса требуется выполнить следующее:
- рассмотреть не только проверяемую гипотезу, но и исключающую ее альтернативную гипотезу;
- выбрать статистический критерий, по которому дается заключение о наличии или отсутствии проверяемой или альтернативной гипотезы.
Чаще всего используют так называемую нулевую гипотезу (Н0), т.е. предположение о том, что между генеральными параметрами сравниваемых групп разница равна нулю и различия, наблюдаемые между выборочными показателями, носят случайный характер (т. е. обусловлены случайным характером формирования совокупности).
Критерии проверки статистических гипотез
Истинность принятой гипотезы проверяют с помощью критериев значимости, т.е. специально выработанных случайных величин, функции, распределения которых известны. Для каждого критерия составлена таблица, в которой содержатся критические точки, отвечающие определенным числам (k,ν) и принятым уровням значимости.
Уровень значимости - значение вероятности, при котором различия, наблюдаемые между выборочными показателями можно считать не существенными.
В исследовательских работах обычно пользуются 5%-ным уровнем значимости, которому отвечает вероятность P=0,05.
Схема использования статистических критериев (К) в области лесного дела при строгом доказательстве нулевой гипотезы
К05 > Кф > К01
Не отвергается Отвергается ,
Нулевая гипотеза
где Кф - значение фактически полученного критерия;
К05, К01 - значения критериев на 5% - ном и 1% - ном уровнях значимости.
3.1. Статистическое сравнение эмпирического распределения с теоретическим по критерию χ- квадрат Пирсона
Критерий
χ- квадрат (χ
2) впервые
был предложен К. Пирсоном в 1901 году.
Пользуясь этим критерием можно произвести
оценку различий между эмпирическим и
теоретическим распределением частот.
Он рассчитывается по формуле:
,
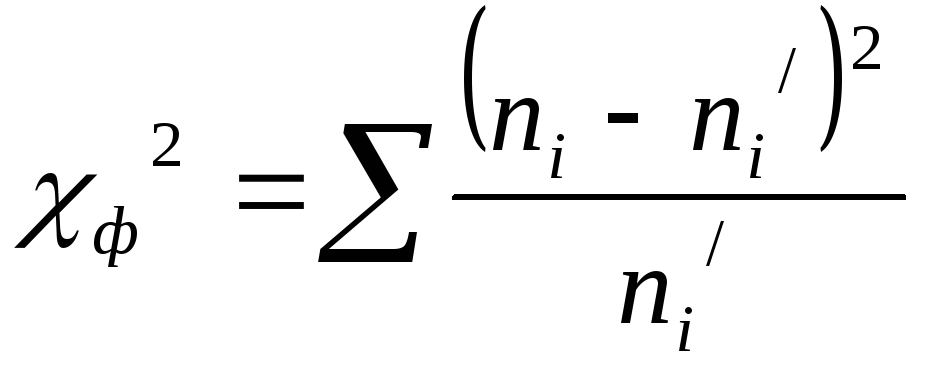где ni – эмпирическая частота; ni'- теоретическая частота.
Оценка значимости критерия χ 2 производится по специальной таблице (приложение 3 учебника Герасимов, Хлюстов), в которой приведены стандартные значения этого критерия (χ 2st) для трех пороговых уровней доверительной вероятности и для разных чисел степеней свободы.
Число степеней свободы равно числу классов без трех k=n-3.
Если χ 2ф< χ 2st , то расхождение между эмпирическим и теоретическим распределением подчиняется тому закону, по которому рассчитаны теоретические частоты.
В таблице 3.1 приводится порядок расчета критерия согласия χ 2 - Пирсона.
Таблица 3.1 Оценка различий между эмпирическим и теоретическим распределением деревьев сосны по диаметру на высоте груди
|
Классы (ступени толщины),см |
Частоты |
ni- ni/ |
(ni – ni/)2 |
| |
|
Эмпирические (ni), штук |
Теоретические (ni/), штук | ||||
|
8 |
2 |
1,63 |
0,37 |
0,14 |
0,08 |
|
12 |
4 |
4,80 |
-0,80 |
0,64 |
0,13 |
|
16 |
11 |
10,55 |
0,45 |
0,20 |
0,02 |
|
20 |
16 |
17,23 |
-1,23 |
1,51 |
0,09 |
|
24 |
30 |
21,27 |
8,73 |
76,28 |
3,59 |
|
28 |
14 |
19,61 |
-5,61 |
31,49 |
1,61 |
|
32 |
10 |
13,51 |
-3,51 |
12,33 |
0,91 |
|
36 |
8 |
7,06 |
0,94 |
0,89 |
0,13 |
|
40 |
3 |
2,73 |
0,27 |
0,07 |
0,03 |
|
44 |
2 |
0,79 |
1,21 |
1,47 |
1,86 |
|
Cумма |
100 |
100 |
|
|
8,44 |
Теоретические частоты берутся неокругленными из таблицы 3.1.
χ 2ф = 8,44
Число степеней свободы k = 10 – 3 = 7, тогда χ 205/01 =14.10/18.50 (на 5 % и 1 % уровне значимости)
Далее сравниваем фактическое значение критерия с теоретическим
χ 2ф < χ 205. , из чего следует, что Н0- гипотеза не отвергается, различия между эмпирическим и теоретическим распределением частот несущественны.