Глава 9. Ряды.

Определение. Пусть ,, ...., , ... бесконечная числовая последовательность. Выражение называется числовым рядом, ,, ...., , ... члены ряда, - общий член ряда.

Необходимый признак сходимости:

Если ряд сходится, то .

Первый признак сравнения.

Пусть даны два ряда (А) и (В), причем каждый член ряда (А) не превосходит соответствующего члена ряда (В), т.е. . Тогда если сходится ряд (В), то сходится и ряд (А); если расходится ряд (А), то расходится и ряд (В).

Интегральный признак Коши.

Если при -непрерывная, положительная и монотонно убывающая функция, то ряд , где , сходится или расходится в зависимости от того, сходится или расходится интеграл .

Признак Даламбера.

Если для ряда существует , то этот ряд сходится при и расходится при .

Признак Лейбница.

Знакочередующийся ряд сходится, если:

1) члены ряда монотонно убывают, по абсолютной величине

2) , общий член стремится к нулю.

Пример

Написать первые три ряда найти интервал сходимости ряда и исследовать его на сходимость на концах интервала.

Решение:

Беря последовательно , запишем данный ряд в виде:

Для нахождения области сходимости ряда применим признак Даламбера

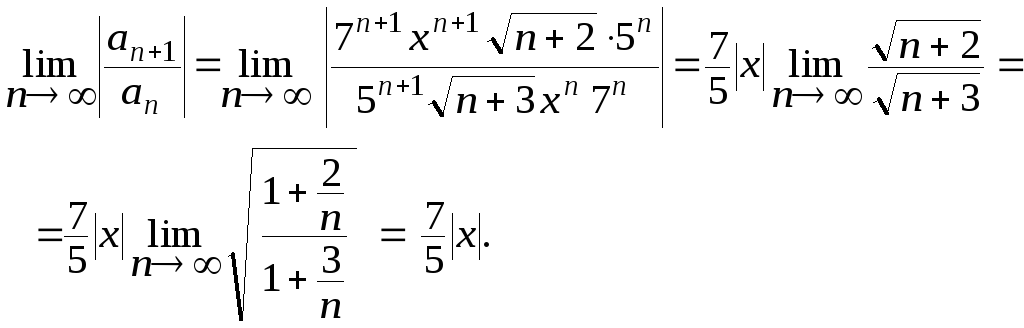
Данный ряд сходится абсолютно при тех значениях , которые удовлетворяют неравенству , или , или .

Исследуем сходимость ряда на концах полученного интервала.

При данный ряд принимает вид это знакочередующийся ряд. Проверим выполнение условий признака Лейбница сходимости знакочередующихся рядов:

1)

2)

Следовательно, по признаку Лейбница ряд сходится. Значит, принадлежит области сходимости данного ряда.

При данный ряд принимает вид . Исследуем сходимость этого числового ряда при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл

.

Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, при исходный ряд расходится.

Таким образом, - область сходимости исходного ряда.

Разложение функций в степенные ряды.

Всякая функция, бесконечно дифференцируемая в интервале , может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора

при получается ряд Маклорена:

Приведем разложения в ряд Маклорена следующих функций:

,

,

,

,

,

Пример

Вычислить с точностью до 0,001 интеграл 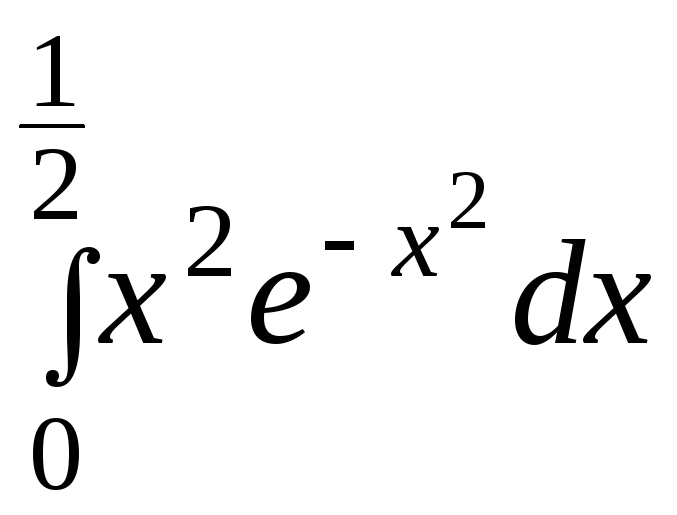путем предварительного разложения подинтегральной функции в степенной ряд и почленного интегрирования этого ряда.

Решение:

В разложении функции в степенной ряд

заменим на.

Тогда получим

Умножая этот ряд почленно на , имеем

. Следовательно,

==

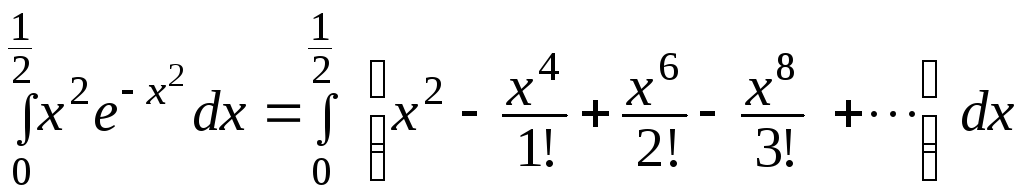Полученный знакочередующийся ряд удовлетворяет условиям признака Лейбница. Третий член этого ряда по абсолютной величине меньше 0,001, поэтому для обеспечения требуемой точности нужно просуммировать первые два члена ряда. Итак,

.

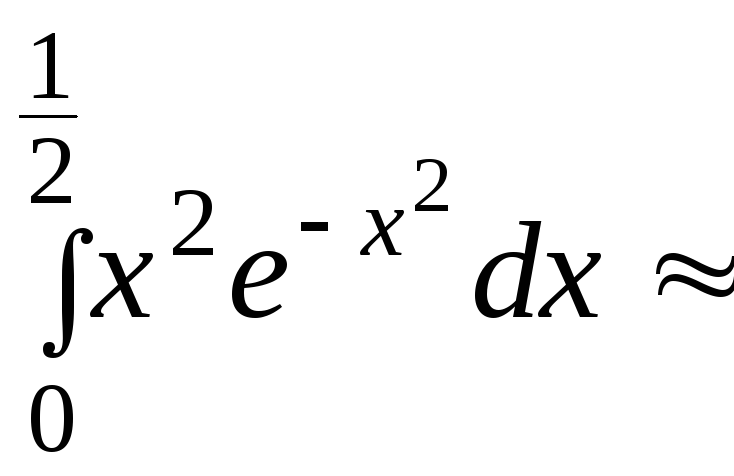
Глава 10. Теория вероятностей