
Кол. методы МБА 2012 / 2. Оптимизация / Книжка по ЛП / 3. Гр.ан.метод 27-44
.pdf
типа приведены в табл. 3.1. Там же указаны недельные запасы ресурсов, которыми располагает фабрика.
Требуется сформировать недельную производственную программу, при которой доход от реализации будет максимальным и в то же время реализацию этой производственной программы можно будет обеспечить имеющимися запасами ресурсов.
Таблица 3.1.
Необходимые |
Кроссовки |
Тапочки |
Недельные запасы |
ресурсы |
|
|
ресурса |
Кожа (кв.ед.) |
7 |
2 |
700 |
Ткань (кв.ед.) |
2 |
4 |
480 |
Труд (ч/час) |
2 |
2 |
300 |
Доход от продажи од- |
100 |
50 |
|
ной пары обуви (руб) |
|
||
|
|
|
Решение
Обозначим через x1 недельный объем выпуска кроссовок, а через x 2 – недельный объем выпуска тапочек. Тогда (x1, x 2 ) – недельная
производственная программа.
При производственной программе (x1, x 2 ) недельный доход от
реализации обуви будет равен |
|
Z =100 x1 +50 x 2 . |
(3.4) |
Для реализации производственной программы необходимо, чтобы затраченные на производство ресурсы не превысили имеющихся запасов. Поэтому выбор x1 и x 2 должен быть таким, чтобы не наруша-
лись ограничения
•по запасу кожи - 7x1 +2x 2 ≤ 700 ,
•по запасу ткани - 2x1 +4x2 ≤ 480 ,
•по запасу трудовых ресурсов - 2x1 +2x2 ≤ 300 .
Кроме того, переменные не могут быть отрицательными числами, т.е. x1 ≥ 0, x2 ≥ 0..
Таким образом, получаем классическую задачу линейного программирования – необходимо максимизировать целевую функцию (3.4) при условии, что переменные удовлетворяют системе ограничений
(3.5).
37
7x1 +2x |
2 ≤ 700, |
|
||
|
+4x |
2 |
≤ 480, |
(3.5) |
2x1 |
||||
|
+2x |
2 |
≤ 300, |
|
2x1 |
|
|||
x1, x 2 ≥ 0.
Это задача с двумя переменными и для ее решения можно использовать графоаналитический метод.
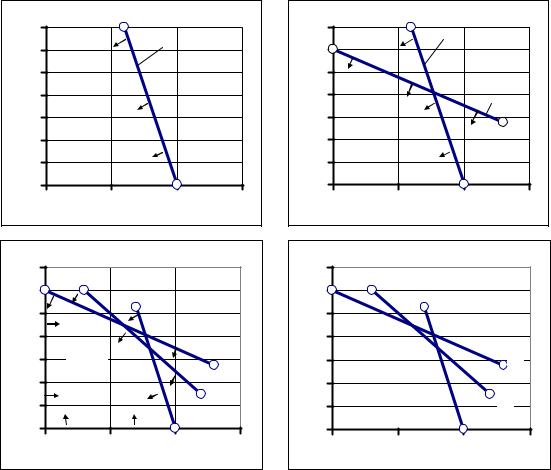
Вначале найдем ОДР, все точки которой, удовлетворяют системе ограничений (3.5). Для этого в координатной плоскости строим гра-
ничные прямые «1», «2», «3» (рис 3.9. a, b, c)
1.7x1 +2x2 = 700 ,
2.2x1 +4x2 = 480,
3.2x1 +2x2 = 300 .
140 |
X2 |
|
1 |
a |
120 |
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
80 |
|
|
|
|
60 |
|
|
|
|
40 |
|
|
|
|
20 |
|
|
|
X1 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
50 |
100 |
150 |
140 X2 |
|
|
c |
|
120 |
|
|
1 |
|
100 |
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
60 |
|
ОДР |
|
2 |
40 |
|
|
||
|
|
|
3 |
|
20 |
|
|
|
|
|
|
|
X1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
50 |
100 |
150 |
140X2 |
|
1 |
b |
|
120 |
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
80 |
|
|
|
2 |
60 |
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
20 |
|
|
|
X1 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
50 |
100 |
150 |
140 |
X2 |
|
|
d |
120 |
|
|
1 |
|
100 |
|
|
|
|
|
|
|
|
|
80 |
|
|
|
2 |
60 |
|
ОДР |
|
|
|
|
|
||
40 |
|
|
|
|
|
|
|
3 |
|
20 |
|
|
|
|
|
|
|
X1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
50 |
100 |
150 |
Рис. 3.9. Построение ОДР для системы ограничений (3.5).
Определяем путем подстановки те полуплоскости, которые удовлетворяют каждому из ограничений. Пересечение полуплоскостей зада-
38
ет искомую ОДР, соответствующую системе ограничений (3.5). По- |
||||||||
следовательность этапов построения ОДР показана на рис. 3.9. a, b, c, |
||||||||
d. Стрелками указаны области (полуплоскости), удовлетворяющие со- |
||||||||
ответствующим ограничениям. |
|
|
|
|
||||
Вектор, |
указывающий |
направление |
роста |
целевой |
функции |
|||
Z =100 x1 +50 x 2 , имеет координаты g ={100,50}. Дадим Z какое- |
||||||||
либо произвольное значение, например Z=4000. Тогда, уравнению ли- |
||||||||
нии |
уровня |
Z=4000 на графике будет соответствовать |
прямая |
|||||
100 x1 +50 x2 = 4000 (рис. 3.10.). Чем далее прямая будет переме- |
||||||||
щаться в направлении g , тем большие значения будет принимать Z. |
||||||||
|
X2 |
|
|
|
|
|
|
|
|
140 |
|
|
|
|
|
|
|
|
120 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
Оптимальная точка |
|
|||
|
|
x |
2opt = 70 |
|
||||
|
80 |
|
|
|
|
|
||
|
60 |
|
|
|
|
|
|
|
|
40 |
|
ОДР |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
g |
Z=4000 |
|
|
|
3 |
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
Zmax=11500 |
X1 |
|
|
|
x1opt =80 |
|
|
|
||
|
0 |
|
50 |
100 |
|
|
150 |
|
|
|
|
|
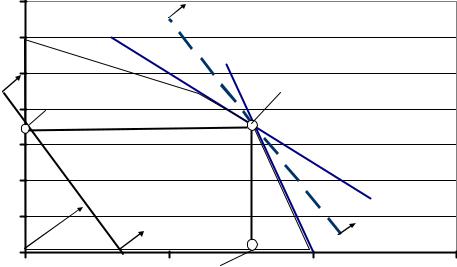
Рис. 3.10. |
|
|
|
|
Область, в которой возможны перемещения линий уровня, ограни- |
||||||||
чена многоугольником ОДР. Следовательно, |
наибольшее значение |
|||||||
будет достигнуто в крайней точке ОДР. Эта точка – (x1opt , x2opt ) – |
||||||||
рис. 3.10. Именно в ней и находится оптимальное решение, при кото- |
||||||||
ром Z примет наибольшее из всех возможных в данной ОДР значений. |
||||||||
Как следует из рис. 3.10, точка оптимума, в которой Z принимает |
||||||||
наибольшее значение – это точка пересечения двух граничных пря- |
||||||||
мых «1» и «3», т.е. 7x1 +2x 2 = 700 и 2x1 +2x2 = 300 . Для того чтобы |
||||||||
найти координаты оптимальной точки, одновременно принадлежащей |
||||||||
как первой, так и третьей прямой, необходимо решить систему урав- |
||||||||
нений |
|
|
|
|
|
|
|
|
|
|
|
|
39 |
|
|
|
|
7x1 +2x 2 = 700,2x1 + 2x 2 = 300.
Решая ее, находим
x1opt =80 , x2opt = 70.
Максимальное значение целевой функции при такой производственной программе будет равно
Zmax =100 x1opt +50 x2opt =8000 +3500 =11500 .
Таким образом, задача решена.
•Кроссовки необходимо выпускать в количестве x1opt =80 пар, тапочки в количестве x2opt = 70 пар.
•При такой производственной программе доход будет максимальным и составит Zmax =11500 руб.
•Все ресурсные ограничения будут выполнены (запасов ресурсов хватит для реализации производственной программы).
3.4. Особенности решения задач линейного программиро- |
|||||||
вания в зависимости от области допустимых решений и |
|||||||
целевой функции |
|
|
|
||||
Отметим некоторые важные особенности задач линейного про- |
|||||||
граммирования и их решений, которые характерны не только для слу- |
|||||||
чая двух управляемых переменных. |
|
||||||
Как было установлено выше, область допустимых решений в зада- |
|||||||
чах линейного программирования |
|
||||||
(ЗЛП) определяется системой огра- |
X2 |
||||||
ничений. В задачах с двумя |
|||||||
|
|||||||
переменными система ограничений |
|
||||||
задает |
на |
плоскости |
некоторую |
|
|||
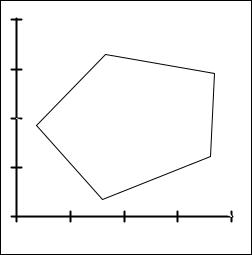
область – многоугольник (рис. |
|
||||||
3.11). |
|
В |
реальных |
задачах |
в |
ОДР |
|
зависимости |
от вида |
ограничений |
|
||||
могут встречаться случаи, когда |
|
||||||
этот |
многоугольник |
может быть |
X1 |
||||
незамкнутым, состоять из одной |
|
||||||
точки или вообще не существовать. |
Рис. 3.11. |
||||||
Пример, когда все граничные |
|||||||
|
|||||||
прямые пересекаются в одной точке показан на рис. 3.12. Это так |
|||||||
|
|
|
|
|
40 |
|
|
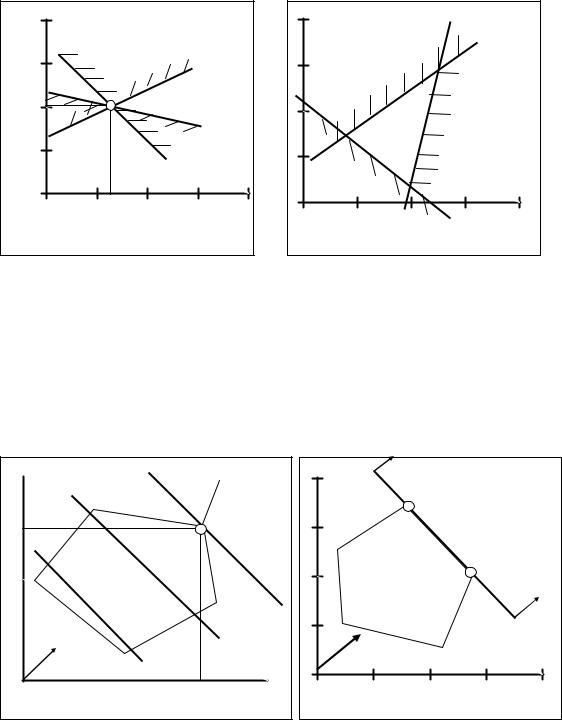
называемый тривиальный случай, когда область допустимых решений состоит из единственной точки, которая и является формальным оптимумом.
X2 |
x2opt |
X1 |
x1opt |
Рис. 3.12. |
X2 |
ОДР |
|
X1 |
|
Рис. 3.13. |
В ряде задач система ограничений ЗЛП может содержать противоречивые условия. Тогда система неравенств не будет иметь общих решений (рис. 3.13.). Геометрически это означает, что области допустимых решений не существует. Очевидно, что говорить о решении задачи с несуществующей ОДР также не имеет смысла.
Решение задачи линейного программирования можно получить, только сопоставляя ОДР и поведение в ней целевой функции. В тех случаях, когда область допустимых решений – замкнутый много-
X2 |
Точка оптимума |
|
x2opt |
|
|
|
|
Z max |
|
ОДР |
|
g |
Z1 |
Z2 |
|
X1 |
|
|
Рис. 3.14. |
x1opt |
|
|
|
X2 |
A |
|
|
|
|
E |
|
|
|
|
B |
|
ОДР |
|
D |
|
Z max |
g |
C |
X1 |
|
Рис. 3.15. |
|
угольник, оптимальное решение как было установлено выше, всегда достигается не во внутренних точках ОДР, а в одной из точек, при-
надлежащей ее границе. При этом, в принципе, возможны два случая.
41
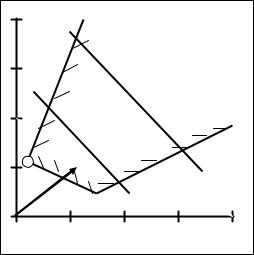
1.Оптимальное решение единственно и оно находится в одной из вершин многоугольника ограничений (рис. 3.14.).
2.В ряде задач может оказаться так, что линия уровня, соответствующая максимальному значению целевой функции в точности совпадает с одной из сторон многоугольника ограничений. В этом случае оптимальными решениями (максимизирующими Z) будут все точки, принадлежащие этой стороне. Пример такой задачи показан на рис. 3.15. Для реальных задач наличие таких альтернативных оптимумов крайне благоприятно, т.к.
позволяет достичь наилучшего ре- |
X2 |
|
|
|||
зультата не единственным спо- |
|
|
|
|||
собом. |
|
|
|
|
|
|
В тех случаях, когда ОДР не |
|
|
|
|||
замкнута, решения может не |
|
|
|
|||
существовать, как, например, при |
|
|
|
|||
поиске |
максимального |
|
значения |
M |
|
Z2 |
целевой |
функции |
в |
ОДР, |
|
||
g |
|
|||||
показанной на рис. 3.16. С другой |
Z1 |
X1 |
||||
стороны, если в этой же задаче, |
|
|
|
|||
требуется найти минимум целевой |
|
Рис. 3.16. |
|
|||
функции, то, как следует из рис. |
|
|
||||
|
|
|
||||
3.16, решение существует, оно будет единственным и расположено в |
||||||
точке М. |
|
|
|
|
|
|
3.5. Понятие о симплекс методе
Выявленные особенности справедливы и положены в основу вычислительных алгоритмов, предназначенных и для решения задач линейного программирования со многими переменными, которые не имеют такой ясной геометрической интерпретации.
В основу симплекс метода и его многочисленных модификаций, применяемых сегодня для решения большинства реальных задач со многими переменными, положены следующие принципы.
•Решение задачи ЛП, если оно существует, всегда находится на границе ОДР.
•Если оптимальное решение, максимизирующее (минимизирующее) целевую функцию, единственно, то оно всегда достигается в одной из вершин ОДР.
42
•Для того чтобы найти оптимальное решение, достаточно перебрать все вершины многогранника и выбрать ту, в которой целевая функция принимает максимальное (минимальное) значение. Такие решения, находящиеся в вершинах многогранника, называют опорными решениями.
•Этап нахождения опорных решений – координат вершин ОДР, является составной частью любого алгоритма поиска оптимального решения.
•Алгоритм перебора опорных решений для поиска оптимума в симплекс методе организуется целенаправленно, так, чтобы при переходе от одной вершины к другой значение целевой функции неуклонно возрастало (убывало).
•Если на одном из этапов переход к соседним вершинам ОДР не приводит к росту (уменьшению) целевой функции, то поиск прекращается, а найденное опорное решение является оптимальным.
Вычислительные алгоритмы поиска оптимальных решений в задачах линейного программирования сегодня реализованы в качестве многочисленных программ для ЭВМ, в том числе и в виде специальной надстройки в MS Excel. Все они используют относительно простые, однако слишком громоздкие при «ручном» счете, итерационные процедуры. Вначале решаются системы линейных уравнений для нахождения опорных решений. Затем найденные опорные решения целенаправленно перебираются.
Вычисления проводятся следующим образом. Вначале программы «находят» некоторое исходное опорное решение и вычисляют для него значение целевой функции. Затем просматриваются соседние вершины и проверяется, улучшается значение целевой функции при переходе в одну из них или нет. Если улучшается, то новая вершина берется за основу и процедура повторяется. Поиск решения прекращается, если переход в соседние вершины не приводит к улучшению. В этом случае найденное решение является оптимальным, и улучшить его в «рамках» данной ОДР уже нельзя.
Автором (основоположником) симплекс метода принято считать Дж. Данцига, который разработал и впервые применил его в 1947 г. Однако первые результаты в этой области были получены академиком Л.В. Канторовичем почти на 10 лет ранее. В силу малой развитости теории линейного программирования в то время, Дж. Данциг, ничего не зная о работах Канторовича, разработал свой метод самостоятельно. Принципиальным отличием предложенного им подхода от неупо-
43
рядоченного перебора опорных решений явился алгоритм целенаправ-
ленного последовательного улучшения решений с учетом изменения целевой функции. Это позволило существенно сократить объемы вычислений при поиске оптимальных решений и сделало метод основным инструментом для решения большинства практических задач линейного программирования. Более подробно вычислительные итерационные процедуры, реализующими симплекс метод, освещены в ра-
ботах [5, 9, 10].
44
