13.4. Скольжение и его влияние на параметры ротора

Из приведенной формулы следует, что скольжение асинхронного двигателя изменяется в диапазоне 0 s 1.

В режиме работы двигателя без нагрузки на валу (режим холостого хода) ротор вращается с частотой лишь немного меньше частоты вращения магнитного поля, которую в дальнейшем будем называть синхронной частотой. В этом случае скольжение весьма мало отличается от нуля. Однако ток холостого хода статора примерно на порядок больше тока холостого хода трансформатора. Напомним, что ток холостого хода трансформатора составляет (2...8) % от номинального значения тока первичной обмотки. Ток холостого хода двигателя составляет (20...40) % от номинального тока статора. Такое увеличение тока холостого хода объясняется тем, что воздушный зазор между статором и ротором увеличивает магнитное сопротивление цепи двигателя для магнитного потока.

Скольжение, соответствующее номинальной нагрузке двигателя, называют номинальным скольжением. Для асинхронных двигателей номинальное скольжение составляет (1…8) %. Меньшие значения соответствуют двигателям большей мощности, большие значения скольжения соответствуют двигателям малой мощности.

Частота вращения ротора (об/мин) может быть определена, если известны синхронная частота магнитного поля статора и скольжение:

n = n1 ( 1 s ) .

Например, для двигателя общепромышленного назначения (f =50 Гц), имеющего четыре полюса и номинальное скольжение 4 %, частота вращения

синхронной частоты и частоты вращения ротора, называется частотой

умножить на значение синхронной частоты, то получим возможность вы-

181

Для f1 = 50 Гц и скольжения s = (2...8) % частота f2 = 1…4 Гц.

Влияние частоты скольжения проявляется на параметрах ротора: ЭДС и реактивном сопротивлении. Выражение для ЭДС обмотки ротора имеет вид E2S = 4,44w2f2Фmкoб, где коб коэффициент, учитывающий специфику выполнения обмотки ротора (обмоточный коэффициент).

Вслучае неподвижного ротора, когда s = 1, частота скольжения f2 равна частоте питающего двигатель напряжения. Поэтому E2S = E2.

Вслучае вращающегося ротора, когда f2 = f1 s, выражение для ЭДС при-

мет вид E2S = 4,44w2fФmko6s = E2 ּs.

Аналогичную связь можно установить и между индуктивными сопротивлениями неподвижного x2S и вращающегося ротора х2:

x2S = x2ּs

Пример 13.1. Для трехфазного асинхронного двигателя известно, что при частоте f1 = 50 Гц. ЭДС и индуктивное сопротивление неподвижного ротора равны: Е2 =120 В., х2 =130 Ом.

Определить значения f2S, Е2S и х2S при скольжении s = 4 % . Воспользовавшись вышеприведенными формулами, получим:

f2S = f1 ּs = 2 Гц; E2S = E2 ּs = 4,8 В; x2 = x2ּs = 5,2 Ом.

13.5. Механическая мощность асинхронного двигателя

Трехфазный асинхронный двигатель нагружает питающую активной мощностью Р1 = 3UФIФcosφФ = 3U лI л cos Ф . Здесь индексом " ф " обозначены

фазные значения напряжения и тока обмотки статора; индексом " л " линейные значения напряжения питающей сети и тока, потребляемого двигателем.

Вдальнейшем будем обозначать индексом 1 параметры обмотки статора,

аиндексом 2 параметры обмотки ротора.

Процесс преобразования электрической энергии в механическую наиболее просто показать в виде энергетической диаграммы (рис. 13.8). На каждой ступени передачи происходят соответствующие потери энергии, обозначенные отдельными ручейками. Эта энергия считается потерянной, а отдельные ее составляющие называются потерями мощности.

На основании энергетической диаграммы двигателя можно определить механическую мощность РМЕХ, отдаваемую двигателем, путем вычитания из

182

подведенной от сети мощности потерь на всех ступенях передачи. К ним относятся потери в обмотке статора, стали сердечника и потери в обмотке ротора.

Уравнение энергетического баланса двигателя запишем в виде

РМЕХ = 3U1I1 соsφ1 - 3I1 r12 pCT m2 I 2 r12 ,

где m2 число фаз обмотки ротора в случае фазного способа его исполнения или число стержней ротора, деленное на два, если обмотка ротора выполнена короткозамкнутой; рСТ потери в стали статора.

Потерями в стали ротора обычно пренебрегают по причине малой частоты тока ротора.

Электромагнитная мощность Рэм, передаваемая ротору, определяется произведением числа фаз, ЭДС, тока и коэффициента мощности ротора. Часть этой мощности выделяется в роторе в виде теплоты.

Рис. 13.8

Таким образом, механическую мощность асинхронного двигателя можно определить как разность между электромагнитной мощностью и потерями в обмотке ротора:

Рмех = m2Е2I2соsφ2 - m2 I 22 r2 .

Это уравнение можно представить в ином виде, если учесть, что Е2 = E2S / s, а произведение E2S соsφ2 = I 22 r2 определяет активную составляющую ЭДС ротора. На основании изложенного выражение для механической мощности примет вид Рмех = m2 I 22 r2 / s m2 I 22 r2, или после некоторого преобразования окончательно запишем:

Рмех = m2 I 22 r2 (1 s)/ s.

Если последнее выражение представить в виде sРмех / (1 s) = m2 I 22 r2 ,

то становится очевидным тот факт, что с увеличением скольжения увеличивается нагрев ротора.

183

Поэтому современные асинхронные двигатели рассчитываются так, чтобы в рабочем режиме скольжение было минимальным.

Полезная механическая мощность на валу двигателя Р2 меньше механической мощности Рмех, развиваемой двигателем, нa величину механических потерь, определяемых трением в подшипниках, а также трением ротора о воздух.

13.6. Вращающий момент и его зависимость от скольжения

Вращающий момент двигателя связан с механической мощностью и угловой частотой вращения ротора известной из механики формулой

М РМЕХ / 2 .

Механическая мощность и ее зависимость от параметров ротора с учетом полученных выше соотношений может быть представлена в виде следующего соотношения:

Рмех = m2Е2I2соsφ2(1 s).

Связь между угловой частотой вращения ротора и магнитным полем статора может быть выражена через скольжение 2 1 (1 s). Если обмотка ста-

тора имеет одну пару полюсов, то 1 , т. е. угловая частота вращения магнитного поля статора равна круговой частоте тока. Однако в общем случае двигатель имеет несколько пар полюсов. Тогда 1 /р , а выражение для угловой частоты ротора примет вид 2 = ( 1 s ) / р .

Учитывая это обстоятельство, выражение для вращающего момента запишем в виде М = (рm2/ )Е2I2соsφ2. Обозначив отношение, стоящее в скобках, как некоторую постоянную СМ, запишем выражение для вращающего момента в виде

М = СМ Е2I2соsφ2.

Анализ полученного выражения показывает, что вращающий момент двигателя пропорционален произведению тока и ЭДС ротора и углу сдвига фаз между ними. Покажем влияние скольжения на отдельные сомножители, опре-

184

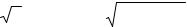
13.7. Коэффициенты мощности и полезного действия асинхронного двигателя

Преобразование электрической энергии в механическую сопряжено не только с потреблением активной и реактивной мощностей, но и с потерями энергии. По этой причине коэффициенты мощности ( cosφ1) и полезного действия (η) асинхронного двигателя не остаются постоянными. Рассмотрим этот вопрос более подробно.

Изменение коэффициента мощности в процессе работы асинхронного двигателя обусловлено изменением составляющих тока статора. Реактивная составляющая тока статора не зависит от нагрузки на валу двигателя и при любом напряжении сети практически неизменна. В то же время, активная составляющая тока двигателя пропорциональна его механической нагрузке. Это приводит к тому, что с увеличением нагрузки относительное значение реактивного тока убывает, а коэффициент мощности увеличивается. При холостом ходе двигателя его коэффициент мощности довольно низок порядка 0,2...0,3. С увеличением нагрузки он быстро возрастает и достигает максимального значения 0,7…0,9 при номинальной нагрузке.

При увеличении нагрузки двигателя свыше номинального значения увеличивается реактивная составляющая тока и коэффициент мощности начинает уменьшаться. Причиной увеличения реактивной составляющей тока является влияние магнитных потоков рассеяния, что и приводит к увеличению реактивной мощности двигателя.

Значение коэффициента мощности трехфазного асинхронного двигателя можно вычислить по формулам

Коэффициент полезного действия ( КПД ) определяется отношением полезной мощности Р2 к подводимой Р1. Следует помнить, что полезной является механическая мощность, развиваемая двигателем на его валу, тогда как подводимая мощность является электрическим параметром и определяется произведением напряжения, тока и коэффициента мощности.

Из приведенной выше энергетической диаграммы следует, что мощность Р1 равна сумме полезной мощности и всех видов потерь в двигателе

Р1 = Р2 + РП .

Потери мощности можно разделить на постоянные, практически не зависящие от нагрузки, и от нее зависящие - переменные. К группе постоянных потерь относятся потери в стале сердечника от гистерезиса и вихревых токов, а

186

также механические потери. Эти потери определяются экспериментально из опыта холостого хода. Переменными потерями являются потери, обусловленные сопротивлением проводников протекающему по ним току:

Р1 = 3 I12 r1; Р2 = m2 I 22 r2, Вт.

КПД двигателя (о.е.) можно вычислить по формуле

η = (Р2 + РП ) / Р1.

Максимальное значение КПД достигается при равенстве постоянных и переменных потерь. Обычно максимум КПД имеет место при нагрузке, равной 75 % от номинальной. Это объясняется тем, что двигатели проектируются с учетом того обстоятельства, что в процессе эксплуатации они не всегда полностью загружены.

13.8. Расчет механической характеристики двигателя по паспортным данным

Основными точками механической характеристики асинхронного двигателя являются: номинальный, пусковой и максимальный моменты, а также соответствующие им частоты вращения. Покажем, как, пользуясь информацией, приведенной в паспорте двигателя, можно рассчитать характерные точки механической характеристики. В табличке, закрепленной на корпусе статора, приведены значения номинальной механической мощности и частоты вращения ротора. По этим данным можно вычислить значения номинального момента на валу двигателя (Н.м):

где ΩН = πn / зо круговая частота вращения ротора.

Для расчета значений пускового и максимального моментов следует взять справочник по электрическим машинам и найти в нем для данного двигателя два параметра: кратность пускового момента КП и кратность максимального момента КМ. Значения коэффициентов определяются соотношением соответствующих моментов к его номинальному значению:

КП = МП / МН , КМ = МКР / МН .

Из приведенных соотношений, находим значения пускового и макси-

мального моментов: МП = КП МН , ММ = КМ МН .

Скольжение, соответствующее пусковому моменту, равно единице. Следовательно, n = 0 об/мин, т. е. ротор неподвижен. Скольжение, соответствующее максимальному ( критическому ) моменту, вычисляется по формуле

187