
- •1. Информация о дисциплине
- •1.1. Предисловие
- •1.2. Содержание дисциплины и виды учебной работы
- •2. Рабочие учебные материалы
- •2.1. Рабочая программа
- •2.2. Тематический план дисциплины
- •2.3. Структурно-логическая схема дисциплины «Электротехника и электроника. Ч. 1»
- •2.6. Рейтинговая система оценки знаний
- •3. Информационные ресурсы дисциплины
- •3.1. Библиографический список
- •3.2. Опорный конспект
- •ВВЕДЕНИЕ
- •РАЗДЕЛ 1. Основы теории электрических цепей
- •1. Электрическая цепь и ее характеристики
- •1.1. Определение цепи
- •1.2. Графическое изображение электрической цепи и ее элементов
- •1.3. О направлениях действия ЭДС, токов и напряжений
- •1.4. Законы электрических цепей
- •1.5. Параметры электрических цепей
- •1.6. Идеальные элементы электрической цепи
- •2. Цепи постоянного тока
- •2.1. Некоторые особенности цепей постоянного тока
- •2.2. Закон Ома и законы Кирхгофа для цепей постоянного тока
- •2.3. Мощность цепи постоянного тока
- •2.4. Расчет простых цепей постоянного тока
- •2.6. Баланс мощностей цепи постоянного тока
- •3. Цепи синусоидального тока
- •3.1. Основные понятия о синусоидальных процессах
- •3.2. Аналитическая запись синусоидальных токов и напряжений
- •3.5. Закон Кирхгофа в векторной форме записи
- •3.7. Действующие значения синусоидальных токов и напряжений
- •3.8. Элементы в цепи синусоидального тока
- •3.10. Цепь с последовательным соединением R, L, C
- •3.11. Цепь с параллельным соединением R, L и C
- •3.14. Понятие о двухполюсниках и об эквивалентных цепях
- •РАЗДЕЛ 2. Методы расчета электрических цепей
- •4.1. Введение. Основы метода
- •4.2. Комплексные токи и напряжения
- •4.3. Комплексное сопротивление и комплексная проводимость
- •4.4. Комплексная мощность
- •4.5. Законы Кирхгофа в комплексной форме записи
- •4.6. Аналогия с цепями постоянного тока
- •5. Методы расчета сложных цепей синусоидального тока
- •5.1. Введение
- •5.2. Метод контурных токов
- •5.3. Метод узловых напряжений (узловых потенциалов)
- •5.4. Метод эквивалентного источника
- •5.5. Метод наложения
- •5.6. Баланс мощностей цепи синусоидального тока
- •РАЗДЕЛ 3. Резонанс, индуктивно связанные цепи и трехфазные цепи
- •6. Резонансные явления. Индуктивно связанные цепи
- •6.1. Резонансные явления
- •6.3. Резонанс в параллельной цепи из элементов R, L,C (резонанс токов)
- •6.5. Цепь с трансформаторной связью между катушками
- •7. Трехфазные электрические цепи
- •7.1. Введение
- •7.2. Соединение трехфазной цепи звездой
- •7.3. Соединение трехфазной цепи треугольником
- •7.4. Расчет трехфазных цепей
- •7.5. Мощность трехфазной цепи
- •РАЗДЕЛ 4 Несинусоидальные токи, напряжения и переходные процессы
- •8.1. Общие положения
- •8.4. Мощность в цепи при несинусоидальных токе и напряжении
- •8.5. Расчет линейных цепей с несинусоидальными ЭДС
- •9.1. Общие положения
- •9.2. Законы коммутации. Начальные условия
- •РАЗДЕЛ 5. Нелинейные электрические и магнитные цепи
- •10. Нелинейные электрические и магнитные цепи постоянного тока
- •10.1. Нелинейные электрические цепи. Общие положения
- •10.2. Нелинейные сопротивления
- •10.3. Нелинейные свойства ферромагнитных материалов
- •10.4. Нелинейная индуктивность
- •10.5. Нелинейная емкость
- •10.6. Нелинейные электрические цепи постоянного тока
- •10.8. Магнитные цепи с постоянным магнитным потоком
- •11. Нелинейные цепи переменного тока
- •РАЗДЕЛ 6. Электрические машины
- •12. Трансформаторы
- •12.1. Назначение и принцип действия
- •12.2. Холостой ход трансформатора
- •12.3. Нагрузка трансформатора
- •12.4. Схема замещения
- •12.5. Режим холостого хода
- •12.6. Режим короткого замыкания
- •12.7. Внешняя характеристика трансформатора
- •12.8. КПД трансформатора
- •13. АСИНХРОННЫЕ МАШИНЫ
- •13.1. Общие вопросы теории электрических машин
- •13.2. Классификация электрических машин
- •13.4. Скольжение и его влияние на параметры ротора
- •13.5. Механическая мощность асинхронного двигателя
- •13.9. Пуск асинхронных двигателей
- •14. Cинхронные машины
- •14.1. Устройство и принцип действия
- •14.2. Характеристика холостого хода
- •14.3. Внешние характеристики синхронного генератора
- •14.4. Включение синхронного генератора на параллельную работу
- •14.5. Пуск в ход синхронных двигателей
- •14.6. Синхронные компенсаторы
- •15. Машины постоянного тока
- •15.1. Конструктивные особенности машин постоянного тока
- •15.2. Классификация по способу возбуждения
- •15.3. Генераторы постоянного тока
- •15.4. Двигатели постоянного тока
- •15.5. Пуск двигателей постоянного тока
- •15.7. Пример решения задачи
- •РАЗДЕЛ 7. Электрические измерения и приборы
- •16. Электрические измерения и приборы
- •16.1. Общие сведения об электрических измерениях
- •16.2. Эталоны единиц электрических величин
- •16.3. Измерительные приборы
- •16.4. Измерение напряжения переменного тока
- •ЗАКЛЮЧЕНИЕ
- •ГЛОССАРИЙ
- •3.4. Лабораторные работы
- •Общие указания
- •3.5. Практические занятия
- •Общие указания
- •4. БЛОК КОНТРОЛЯ ОСВОЕНИЯ ДИСЦИПЛИНЫ
- •Общие указания
- •ЗАДАЧА 1
- •ЗАДАЧА 2
- •ЗАДАЧА 3
- •ЗАДАЧА 4
- •ЗАДАЧА 5
- •ЗАДАЧА 6
- •ЗАДАЧА 7
- •ЗАДАЧА 8
- •ЗАДАЧА 9
- •4.2. Текущий контроль (вопросы для самопроверки, тестовые задания)
- •Тема 1. Репетиционный тест 1
- •Тема 1. Тест 1
- •Тема 2. Репетиционный тест 2
- •Тема 2. Тест 2
- •Тема 3. Репетиционный тест 3
- •Тема 3. Тест 3
- •Тема 4. Репетиционный тест 4
- •Тема 4. Тест 4
- •Тема 5. Репетиционный тест 5
- •Тема 5. Тест 5
- •Тема 6. Тест 6
- •Тема 7. Репетиционный тест 7
- •Тема 7. Тест 3.7
- •Тема 8. Тест 8.
- •Тема 9. Тест 9
- •Тема 10. Репетиционный тест 10
- •Тема 10 Тест 10
- •Тема 11. Тест 11
- •Тема 12. Тест 12
- •Тема 13. Тест 13
- •Тема 14. Тест 14
- •Тема 15. Тест 15
- •Тема 16. Тест 16
10.4. Нелинейная индуктивность
Характеристикой |
катушки индуктивности |
является зависимость (i) , |
выражающая связь потокосцепления самоиндукции |
и тока i в катушке. |
|
Эта характеристика |
называется вебер-амперной. Если магнитный поток |
|
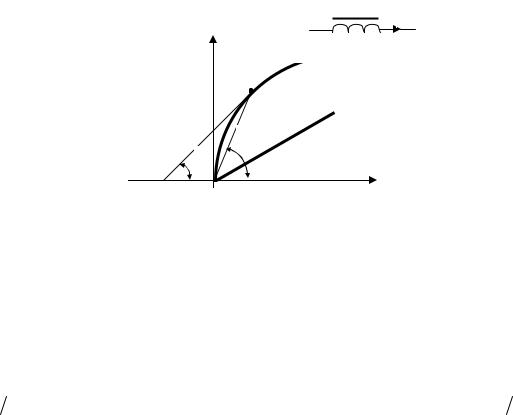
распространяется в линейной среде, например в воздухе, где = 0 = const, то вебер-амперная характеристика линейна (рис. 10.3). Для катушки с ферромагнитным сердечником (i) нелинейна (рис. 10.3), так как магнитная проницае-
мость ферромагнитного материала сильно зависит от напряженности магнитного поля. Вебер-амперная характеристика катушки с замкнутым ферромагнитным сердечником имеет тот же характер, что и начальная кривая намагничивания B(H) материала сердечника.
i
const
|
= const |
|
|
i |
|
0 |
|
|
Рис. 10.3 |
Различают два типа вебер-амперных характеристик статические, получаемые при медленном изменении тока; и динамические, которые полу-
чают при |
достаточно |
быстрых |
изменениях |
тока. |
Динамическая характери- |
|||||
стика отличается от статической из-за |
магнитной |
вязкости и вихревых токов. |
||||||||
Из статической характеристики определяют |
статическую индуктивность: |
|||||||||
LСТ i ; |
из динамической динамическую индуктивность: Ld d di . |
|||||||||
При достаточно медленном изменении |
тока |
статическая |
и динамиче- |
|||||||
ская характеристики катушки совпадают, |
и динамическая индуктивность в |
|||||||||
этом случае равна дифференциальной |
Ld |
d / di , |
определяемой |
из стати- |
||||||
ческой характеристики. |
|
|
|
|
|
|
|
|
||
Статическая индуктивность пропорциональна тангенсу |
угла |
наклона |
||||||||
прямой, проведенной |
из начала |
координат |
в соответствующую точку на ха- |
|||||||
148
рактеристике, а динамическая пропорциональна тангенсу угла наклона касательной в этой точке (рис. 10.3):
LСТ |
|
|
ktg ; |
Ld d |
ktg , |
|
|
i |
|
di |
|
где k отношение масштабов потокосцепления и тока.
10.5. Нелинейная емкость
Самыми распространенными устройствами, которые используются в качестве накопителей энергии электрического поля, являются конденсаторы. Характеристики конденсаторов зависят от свойств диэлектрика, в котором распространяется электрическое поле. В большинстве диэлектриков диэлектрическая проницаемость зависит от напряженности электрического поля E. В этом случае кулонвольтная характеристика конденсатора q(u) нелинейная.
Аналогично нелинейным сопротивлению и индуктивности вводят поня-
тия статической и динамической емкости: |
|
|
||
CСТ |
q |
, |
Cd |
dq . |
|
u |
|
|
du |
Нелинейные емкости применяют, например, в радиоэлектронике.
10.6. Нелинейные электрические цепи постоянного тока
Задача расчета нелинейных электрических цепей постоянного тока значительно сложнее аналогичного исследования линейных электрических цепей. Это связано с тем, что при расчете нелинейных цепей неприменимы принцип наложения и методы, основанные на этом принципе. Для анализа простых нелинейных цепей можно эффективно применять графические методы расчета. При расчете сложных нелинейных цепей с помощью первого и второго законов Кирхгофа составляют системы нелинейных алгебраических уравнений, описывающих процессы в этих цепях. В большинстве случаев получить аналитическое решение таких систем уравнений невозможно. Поэтому для их решения широко используются численные методы расчета.
10.6.1.Расчет электрической цепи при последовательном
ипараллельном соединении нелинейных резистивных элементов
149
Если вольтамперные характеристики нелинейных элементов цепи постоянного тока заданы графическими зависимостями, то расчет такой цепи выполняется графическими методами. Расчет таких цепей производится с использованием законов Кирхгофа.
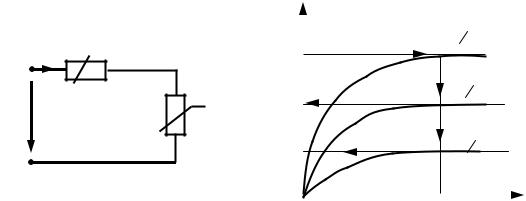
Рассмотрим цепь (рис. 10.4,а) с последовательным соединением нелинейных элементов U1(I) и U2(I) (приведены на рис. 10.4,б в виде кривых 1 и 2).
Согласно второму закону Кирхгофа |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
U = U1 (I) + U2 (I), |
|
|
|
|
|
|
|
|||||
где U приложенное |
напряжение, U1 (I) и U2 (I) |
напряжения на первом и |
||||||||||||||
втором нелинейных элементах. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Элементы соединены |
последовательно, |
и |
в |
них |
протекает одинако- |
|||||||||||
вый ток I. |
Поэтому |
результирующая |
вольтамперная характеристика нели- |
|||||||||||||
нейной цепи U(I) определяется кривой 3 |
на рис. 10.4,б. Она получена в резуль- |
|||||||||||||||
тате сложения ординат кривых 1 и 2 при одних и тех же значениях тока. |
|
|
||||||||||||||
По характеристике U(I) находим значение тока I' в |
цепи |
при заданном |
||||||||||||||
значении |
приложенного |
напряжения |
U'. |
По |
этому значению тока определя- |
|||||||||||
ем падения напряжения U1 |
и U 2 |
на первом и втором элементах по кривым |
||||||||||||||
U1 (I) и U2(I). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
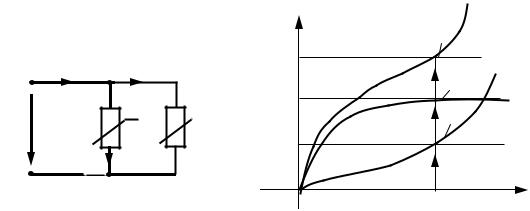
Если элементы |
соединены |
параллельно |
(рис. 10.5,а) |
и |
заданы их |
|||||||||||
вольтамперные характеристики I1 (U) и I2 (U) кривыми 1 и 2 (рис. 10.5,б), то в |
||||||||||||||||
этой цепи по первому закону Кирхгофа |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
I = I1 (U) + I2 (U). |
|
|
|
|
|
|
|
|
||||
Элементы включены параллельно, и напряжения на первом и |
втором |
|||||||||||||||
элементах одинаковы |
и |
равны |
U. |
Поэтому |
вольтамперную характеристи- |
|||||||||||
ку цепи (рис. 10.5,б) |
I (U) |
(кривая |
3) |
можно получить, суммируя |
токи |
|||||||||||
(ординаты кривых) при |
одинаковых значениях U. По кривой I (U) определим |
|||||||||||||||
значение тока I' при заданном U', а по кривым I1 (U) и I2 (U) находим токи не- |
||||||||||||||||
линейных элементов I1 |
и I 2 . |
|
|
|
U |
|
|
|
|
|
|
|
|
|
||
а) |
НЭ1 |
|
|
|
б) |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
||
|
I |
|
|
НЭ2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
U |
U1(I) |
|
|
|
U2 |
|
|
|
|
|
|
|
|
|||
|
|
U2(I) |
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
U1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.4 |
0 |
I |
I |
|
150
а) |
б) |
I |
I2 |
|
U |
НЭ1 |
|
I1 |
НЭ2 |
Рис. 10.5
I |
3 |
|
I |
2 |
|
I2 |
|
|
1 |
|
|
|
|
|
I1 |
|
|
0 |
U |
U |
10.7. Аналитическое представление характеристик нелинейных элементов
Характеристики нелинейных элементов задаются в виде кривых или графиков, построенных по экспериментальным данным. Но для аналитических расчетов нелинейных цепей характеристики элементов должны быть представлены аналитическими выражениями. Процесс замены нелинейной харак-
теристики, заданной графиком |
или |
таблицей, |
приближенным математи- |
|
ческим выражением называется аппроксимацией. |
|
|
||
При подборе математического |
описания нелинейной характеристики |
|||
желательно выполнить следующие условия. |
|
|
||
Во-первых, аппроксимация должна быть по возможности более |
точной. |
|||
Во-вторых, необходимо, чтобы |
аппроксимирующее выражение |
было не- |
||
сложным, так как, чем сложнее |
выражение, тем труднее дальнейшее реше- |
|||
ние уравнения, описывающего нелинейную цепь. |
Поэтому необходим ком- |
|||
промиссный выбор между усложнением функции и точностью приближения.
Наиболее распространенной |
является |
аппроксимация нелинейных харак- |
||
теристик полиномом |
|
|
|
|
y(x) 0 |
1х 2 x2 |
3 x3... n xn . |
||
Такая аппроксимация широко используется |
для |
математического опи- |
||
сания вебер-амперных характеристик |
нелинейных |
индуктивностей i( ) с |
||
ферромагнитными сердечниками. Достаточно |
хорошие результаты по точ- |
|||
ности дает аппроксимация усеченными полиномами вида |
|
|||
i( ) 3 ; |
i( ) 1 3 3. |
|||
|
151 |
|
|
|
