6.Резонансные явления. Индуктивно связанные цепи

Втеме 6 рассматриваются вопросы, входящие в третий раздел рабочей программы. Для изучения данной темы следует иcпользовать материал темы 6. Эти вопросы также разобраны в [1], [2], [3].

Обратите особое внимание на ключевые моменты этой темы, которыми являются:

условие возникновения резонанса;резонанс напряжений;

резонанс токов;

закон электромагнитной индукции;

коэффициент взаимной индуктивности;

согласное и встречное включение катушек;

цепь с трансформаторной связью.

6.1. Резонансные явления

Резонансом в цепи, содержащей сопротивления индуктивности и емкости,

называется такой режим, при котором ток и напряжение на входе цепи сов-

падают по фазе. Это обусловлено тем, что реактивные сопротивления и про-

водимости отдельных участков цепи могут быть как положительными, так и отрицательными величинами и, следовательно, взаимно компенсироваться.

Существует резонанс напряжений и резонанс токов.

6.2. Резонанс в последовательной цепи из элементов R, L, C (резонанс на-

пряжений)

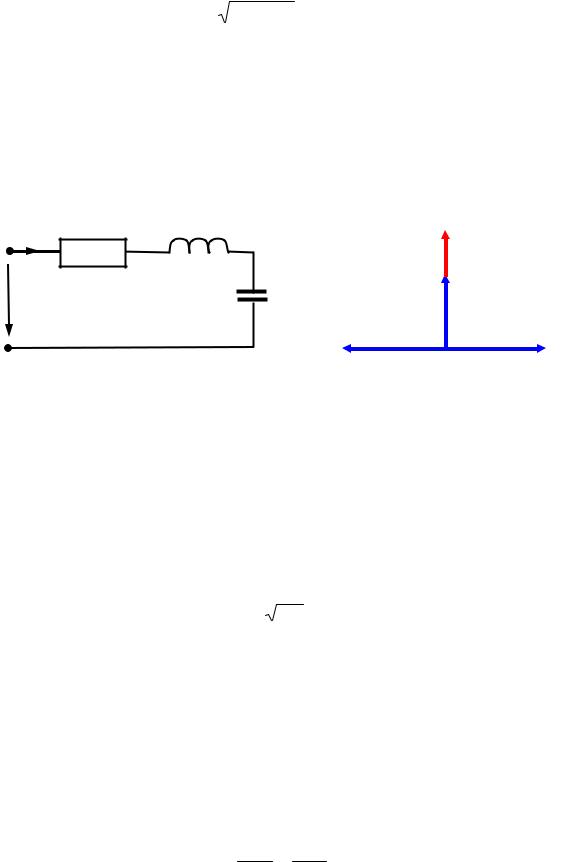
Комплексное сопротивление цепи, состоящей из последовательно соединенных элементов R, L и C (рис. 6.1), имеет вид

101

Резонанс имеет место, как указано выше, при φ = 0, что равносильно при последовательном соединении условию

Резонанса можно достичь, изменяя или частоту приложенного к цепи напряжения, или индуктивности катушки или емкости конденсатора. При этом значения угловой частоты, при которой наступает резонанс, определяется формулой

Частоту ω0 называют резонансной частотой. Если реактивные сопротивления xL xC при резонансе превосходят по величине активное сопротивление R,

превосходить напряжение на зажимах цепи. Поэтому такой резонанс назы-

вают резонансом напряжений.

Отношение

Q UUC 0 UUL0

102

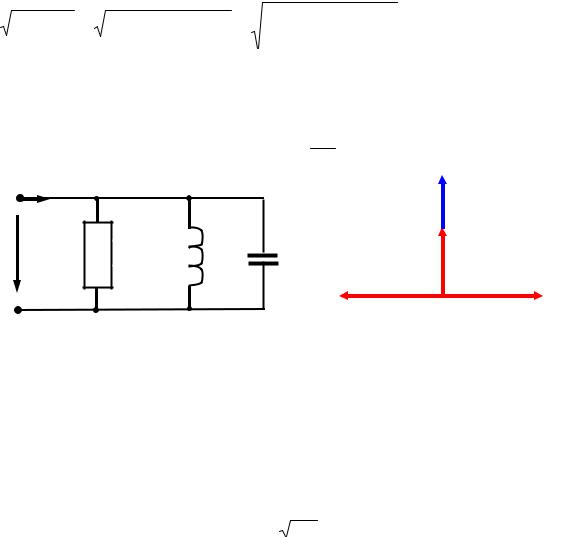
определяет кратность превышения напряжения на индуктивности и на емкости над напряжением на зажимах всей цепи. Величину Q, определяющую резонансные свойства контура, называют добротностью контура

6.3. Резонанс в параллельной цепи из элементов R, L,C (резонанс токов)

Условием резонанса при параллельном соединении активного индуктивного и емкостного сопротивлений (рис. 6.2,а) является также отсутствие сдвига фаз между током и напряжением на входе цепи.

Комплексная проводимость цепи имеет вид

Y g jb ye j , где

Резонанс имеет место, как указано выше, при φ = 0, что равносильно при параллельном соединении условию

Резонанса токов можно достичь, изменяя или частоту приложенного к цепи напряжения, или индуктивности катушки или емкости конденсатора. При этом значения угловой частоты, при которой наступает резонанс, определяется формулой

При резонансе реактивная проводимость цепи равна нулю и полная проводимость цепи достигает своего минимального значения. Поэтому ток в об-

103

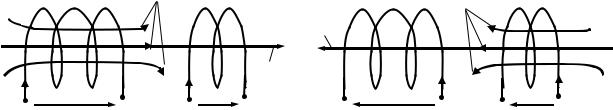
щей ветви I = Uy при неизменном значении оказывается наименьшим в отличие от резонанса с последовательным соединением. Векторная диаграмма при резонансе в рассматриваемой цепи приведена на рис. 6.2,б. При этом токи в индуктивности и в емкости равны и находятся в противофазе. По величине они могут превосходить, а иногда намного, суммарный ток в цепи. Поэтому такой резонанс называют резонансом токов.

определяет кратность превышения токов в индуктивности и токов в емкости над суммарным током всей цепи. Величину Q, определяющую резонансные свойства контура, называют добротностью контура

6.4. Особенности расчета цепей синусоидального тока при наличии взаимных индуктивностей

Если при изменении во времени тока в одной катушке на зажимах второй возникает ЭДC такие катушки называются индуктивно связанными. Это, например, катушки на стальных сердечниках электрических машин и аппаратов, провода линий электропередач, а также многие другие электротехнические устройства.

На рис. 6.3,а показаны две идеальные (без активных сопротивлений) катушки индуктивности.

При протекании в первой катушке синусоидального тока i1 в ней возникает магнитное поле, характеризуемое потокосцеплением самоиндукции L1 w1 , где w1 число витков первой катушки, Ф магнитный поток, проходящий через

104

один виток катушки. Это потокосцепление в соответствии с законом электромагнитной индукции индуцирует в первой катушке ЭДС самоиндукции:

еL1 d L1 / dt .

Напряжение u1 на этой катушке численно равно этой ЭДС, но направлено в противоположную сторону и поэтому имеет обратный знак:

u1 = eL1= + d dtL1 =L didt1 ,

где L1= L1i1, L1 индуктивность первой катушки.

В комплексной форме записи это напряжение имеет вид U1 j L1I1 , где L1 X L1 индуктивное сопротивление первой катушки.

При наличии магнитной связи между катушками 1 и 2 , некоторая часть потокосцепления самоиндукции первой катушки L1 проникает во вторую ка-

тушку. Эта его часть M 21 называется потокосцеплением взаимной индукции второй катушки, вызванное током i1 первой катушки.

Потокосцепление M 21 индуцирует во второй катушке ЭДС взаимной

M 21 к току в первой катушке i1 есть взаимная индуктивность этих кату-

шек: М 21 i1 М21. Взаимная индуктивность также, как и собственная индук-

тивность, измеряется в генри (Гн). С учетом последнего соотношение ЭДС взаимной индукции второй катушки приобретает вид

Аналогичные рассуждения можно привести и для случая, когда синусоидальный ток i2 протекает только по 2-й катушке (рис. 6.3,б). Потокосцепление

самоиндукции L2 второй катушки индуцирует в ней электродвижущую силу самоиндукции еL2 (d L2 dt) . Напряжение на второй катушке равно ей по величине и противоположно по знаку: u2 еL2 d L2 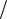dt L2 di2 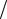dt . Здесь

вую катушку и образует там потокосцепление взаимной индукции M12 . Оно индуцирует в 1-й катушке ЭДС взаимной индукции еM12 d M12 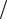dt . Отно-

105

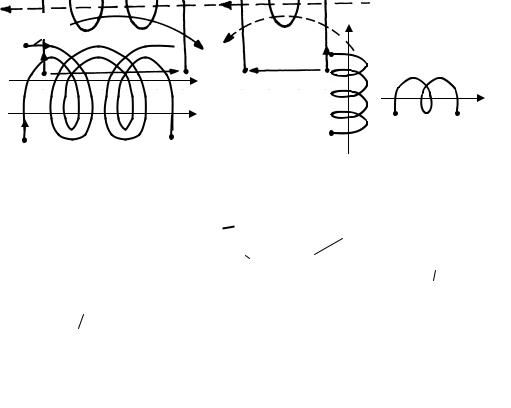
шение потокосцепления взаимной индукции M12 к току во второй катушке i2 есть взаимная индуктивность этих двух катушек: М12 i2 = М12. С учетом этого соотношения ЭДС взаимной индуктивности в первой катушке

еM12 M12 di2 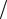dt .

Заметим, что для линейных электрических цепей взаимная индуктивность двух катушек не зависит от того, каким образом она была определена экспериментально:

Она является их общим параметром и не зависит от величин потокосцеплений и токов, а определяется только конструкцией катушек, их взаимным расположением и магнитными свойствами окружающей среды.

Придвигая катушки друг к другу, мы увеличиваем М, а отодвигая их друг от друга – уменьшаем М. Наибольшей взаимной индуктивностью обладают две катушки, навитые одинаково друг на друга (рис. 6.4,а), а наименьшей расположенные своими осями под углом 90 друг к другу (рис. 6.4,б) или далеко удаленные друг от друга.

При одновременном протекании токов в обеих катушках в соответствии с

Рис. 6.5

106