5.Методы расчета сложных цепей синусоидального тока

Втеме 5 рассматриваются вопросы, входящие в третий раздел рабочей программы. Для изучения данной темы следует иcпользовать материал темы 5.

Эти вопросы также разобраны в [1], [2], [3].

Обратите особое внимание на ключевые моменты этой темы, которыми являются:

метод контурных токов;

метод узловых напряжений (узловых потенциалов);

метод эквивалентного источника;

метод наложения;

баланс мощностей цепи синусоидального тока;

комплексная мощность.

85

5.1. Введение

Сложной называют электрическую цепь, имеющую разветвленную структуру и содержащую несколько источников энергии.

В основу расчета (определения токов) будет положено изображение исходных данных цепи комплексными числами. Напомним, что законы Ома и Кирхгофа в комплексной форме выполняются. Поэтому все рассмотренные ниже методы можно использовать для расчета цепей постоянного тока.

Метод расчета, основанный на непосредственном применении 1-го и 2-го законов Кирхгофа, рассматривался во второй лекции для цепей постоянного тока, и поэтому он здесь не представлен.

5.2.Метод контурных токов

Воснове метода лежит представление о независимых контурах, по которым протекают не зависимые друг от друга контурные токи.

Независимым называется контур, который содержит хотя бы одну новую ветвь, не входящую в другие контура.

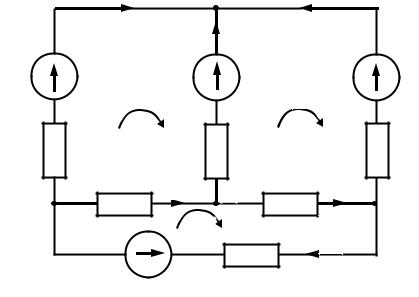
На рис. 5.1 показана схема сложной цепи, в которой можно насчитать семь контуров. В ней можно выбрать только три независимых контура, например, контуры I, II, III. Остальные контуры окажутся зависимыми поскольку каждый из них содержит новые ветви, не входящие в другие контура.

В каждом из трех независимых контуров цепи протекает свой контурный ток. На рис. 5.1 показаны произвольно (по часовой стрелке) принятые направ-ления действия контурных токов İI, İII и İIII в независимых контурах цепи.

Контурные токи – промежуточные неизвестные данного метода рас-

чета. Относительно них составляется система уравнений (используется второй закон Кирхгофа). Легко заметить, что контурных токов меньше, чем токов в ветвях цепи. Это позволяет понизить порядок системы уравнений по сравнению с решением задачи по 1-му и 2-му законам Кирхгофа.

86

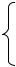
Z11 İI + Z12 İII + Z13 İIII = Ė11

Z21 İI + Z22İII + Z23 İIII= Ė22 .

(5.2)

Z31 İI + Z32 İII + Z33 İIII = Ė33 .

Сумму сопротивлений каждого контура будем называть собственным сопротивлением контура и обозначать для сокращения записи одним сопротивлением с двойным индексом вида ZКК. Для нашего примера имеем следующие собственные сопротивления контуров: Z11=Z1+Z2+Z5; Z22=Z2+Z3+Z6;

Z33=Z5+Z6+Z4. Все собственные сопротивления входят в уравнения (5.2) со знаком (+).

Сумму сопротивления общих для любых двух смежных независимых контуров будем называть взаимным сопротивлением контуров и обозначать его двойной индексацией вида ZКМ. Взаимные сопротивления входят в уравнение для каждого независимого контура со знаком (+), если контурные токи смежных контуров направлены в них в одну сторону (согласно) и со знаком ( ), – если в разные стороны (встречно). В нашем примере взаимное со-

противление первого и второго контуров Z12 = Z21 = Z2; взаимное сопротивление первого и третьего контуров Z13 = Z31= Z5; взаимное сопротивление второго и третьего контуров Z23 = Z32 = Z6 . Все они взяты со знаком ( ) потому, что контурные токи в каждом из смежных контуров направлены встречно друг другу.

Алгебраическую сумму ЭДС каждого независимого контура будем обозначать одной буквой с двойным индексом вида ЕКК . Решая полученную

систему уравнений, находим контурные токи İI ,İII и İIII. Однако на этом решение задачи не завершается, поскольку надо найти еще токи во всех ветвях цепи.

Во внешних ветвях (в нашем примере это ветви с сопротивлением Z1, Z3 и Z4) их токи равны контурным (с учетом знака).

88

Пример 5.1. Два источника энергии (рис. 5.2) работают параллельно на одну нагрузку. Параметры источников и нагрузки известны: Е1 = 120 В;

Ė2=115 В; Z01 = Z02 = (1+j2) Ом; ZН =10 Ом. Требуется определить комплексные токи всех ветвей цепи, используя метод контурных токов.

1. Выбираем (произвольно) направления токов во всех ветвях цепи (İ1, İ2, İН ), как это показано на рис. 5.1.

2. Выбираем в качестве независимых контуры I и II и направления контурных токов İI и İII в них, как это показано на рис. 5.1.

3. Составляем систему уравнений по образцу системы (5.2)

Z11 = Z01+Z02=(1+j2) + (1+j2)= (2+j4) Ом; Z22=Z02+ZН (1+j2)+10 = (11+j2) Ом;

Z12=Z21= Z02= (1+j2) Ом .

4. Рассчитываем контурные токи İI и İII, воспользовавшись теорией определителей.

Главный определитель системы

= (2+j4) (11+j2) (1+j2) (1+j2) =17 + j44 = 47,2е j68,8 .

Первый дополнительный определитель получаем из главного заменой первого столбца свободными членами уравнений:

89