Сигналы с полосовыми спектрами

Если сигнал S(t) непрерывный, имеет полосовой спектр шириной DF₁=f₁-f₂, то его можно представить в виде ортогонального разложения следующего вида:

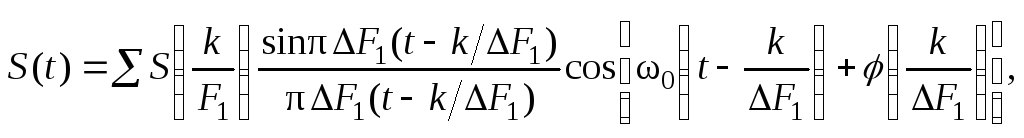
где w₀=2p(f₁+f₂)/2 – среднее значение угловой частоты спектра сигнала; Dt=1/2DF₁; S(k/DF₁); j(k/DF₁) – отсчеты амплитуды и фазы сигнала в моменты t_k=kDt. Из формулы видно, что для сигналов с полосовыми спектрами необходимо через интервал дискретизации отсчитывать мгновенные значения не только амплитуд, но и фаз. Так, в частности, дискретизируют однополосные колебания – сигналы с полосовыми спектрами.

Основные особенности ортогонального разложения Котельникова следующие: базисная система включает совокупность ортогональных функций отсчетов, каждая из которых представляет собой модулированное по амплитуде колебание с несущей частотой w₀ и огибающей, определяемой функцией g_k(t); помимо отсчетов амплитуд берутся отсчеты фаз; если длительность сигнала Т, то число отсчетных точек n=T/Dt=2TDF₁.

В целом, все ортогональные разложения Котельникова – теоретическая основа большинства методов дискретной передачи непрерывных сигналов. Они позволяют с единых позиций рассматривать передачу как дискретных, так и непрерывных сигналов.

Теорема отсчетов в частотной области

При анализе сигналов с непрерывными спектрами часто бывает необходимо представить сигнал с помощью частотных выборок спектральной функции , а не временных выборок функцииS(t).

Для функции можно составить ряд, аналогичный предыдущему выражению , на основании взаимной заменяемости переменныхt и w в паре преобразований Фурье. Это означает, что t следует заменить на w, 2W=2pF на Т, Dt=1/2F на Dw=2p/T.

Таким образом, получаем

.

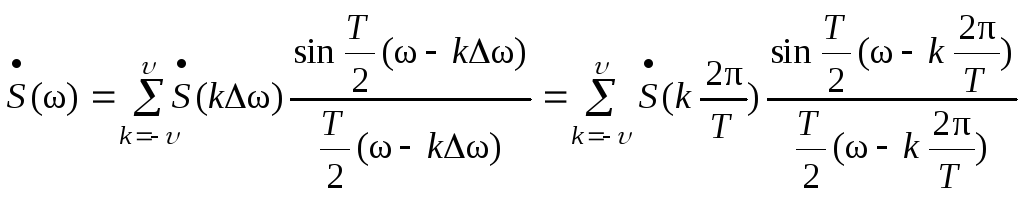Расстановка частотных выборок иллюстрируется следующим рисунком.

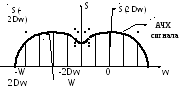
Если ранее временной интервал между двумя соседними выборками не должен был превышать 2p/2W, то теперь частотный интервал не должен превышать 2p/T. При ширине спектра 2W, охватывающей область частот W<W<W, число выборок равно 2W/Dw=2FT, т. е. как и при представлении сигнала рядом.

В общем случае выборки являются комплексными числами, и в каждой отсчетной точке на оси частот должны быть заданы два параметра – действительная и мнимая части, или модуль и аргумент. Таким образом, общее число параметров получается вдвое большим, чем при временном представлении сигнала, когда выборкиS(k/2F) – действительные числа. Избыточность представления сигнала в частотной области легко устраняется, если учесть, что иявляются комплексно-сопряженными функциями, так что задание одной из них однозначно определяет другую. Таким образом, спектр сигнала полностью характеризуется совокупностью комплексных выборок, взятых только в области положительных частот, и числом независимых параметровn=2FT, как и при представлении сигнала во временной области.

1.5. Корреляционные характеристики сигналов

Автокорреляционная (автоковариационная) функция

Выражение

называется корреляционной функцией сигнала (правильнее, автоковариационной) АКФ S(t).

Свойства АКФ:

1) (очевидно),

2) (замена переменных),

3) .

Связь между АКФ и его энергетическим спектром

По определению АКФ определяется выражением

Используя формулу Рэлея, получим

Используя теорему о сдвиге,

подставим в :

т. е. есть обратное преобразование Фурье от . Следовательно, есть прямое преобразование Фурье от :

так как , то - действительная положительная функция, четная

, где

Это способ определения спектральной плотности энергии:

.

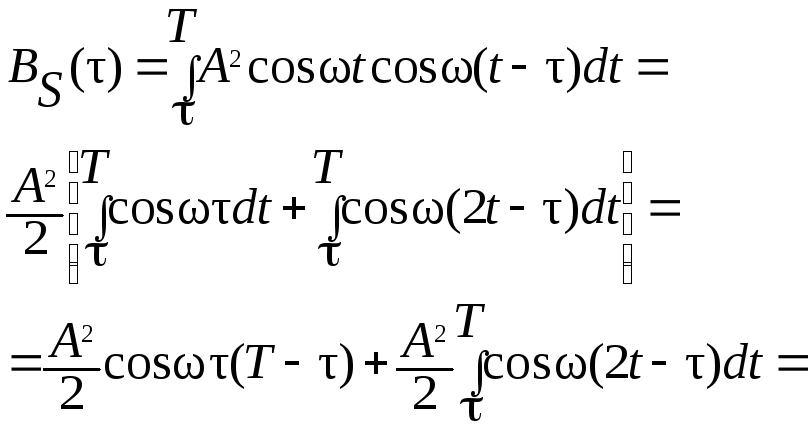
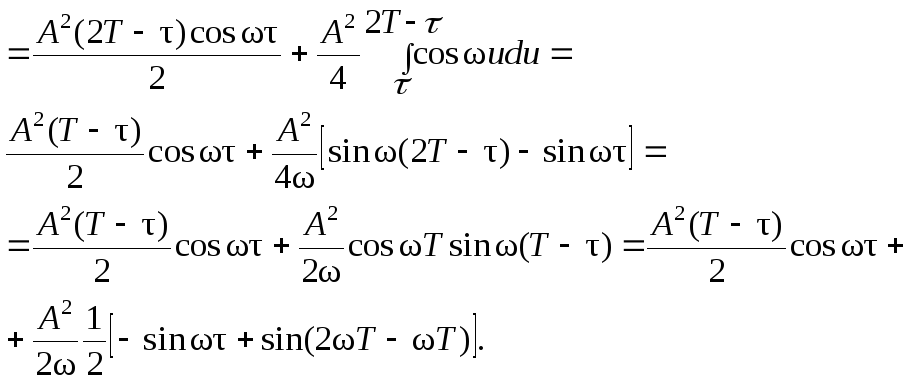Здесь была сделана замена переменных

.

Взаимокорреляционная функция двух сигналов (ВКФ)

Эта функция описывает похожесть или различие сигналов и их взаимное расположение на временной оси.

Пример

,

,

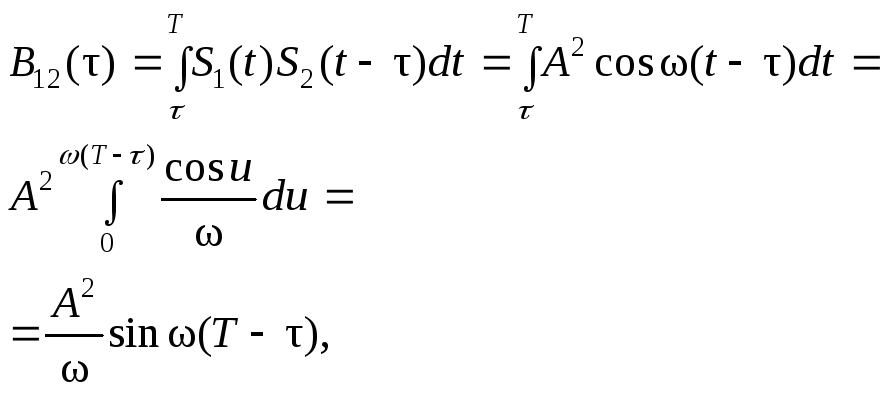
Связь ВФК со взаимной спектральной плотностью

Используя формулу Релея:

Общие свойства сигналов:

1. Сигналы с постоянными параметрами информацию не несут.

2. Чем чаще во времени изменяется сигнал, тем большую информацию он

может нести (примеры – цифровые сигналы, последовательный код). Для передачи большого объёма информации надо использовать высокочастотные сигналы.

3. Чем выше частота сигнала, тем легче его излучать и концентрировать

энергию в нужном направлении.

4. Если сигналы не перекрываются по спектру, то их скалярное произведение равно 0.

5. Если сигналы не перекрываются по времени, то их скалярное произведение равно 0.

6. Некоторые сигналы могут перекрываться и по спектру, и по времени,

но их скалярное произведение равно 0 на ограниченном отрезке времени (пример – разные системы отрезков функций).

7. Некоторые сигналы могут перекрываться и по спектру, и по времени,

но их скалярное произведение равно 0 по всей оси времени (Котельников – время).

8. Некоторые сигналы могут перекрываться и по спектру, и по времени, но их скалярное произведение равно 0 по всей оси частот (Котельников – частота). Но нет перекрытий по времени, так как если Котельников – частота, то во времени – это импульс.