Квадратичный детектор

Напряжение на выходе детектора можно представить в виде ,

где К – коэффициент пропорциональности.

Используя выражение

,

получим закон распределения шумового напряжения на выходе квадратичного детектора:

,

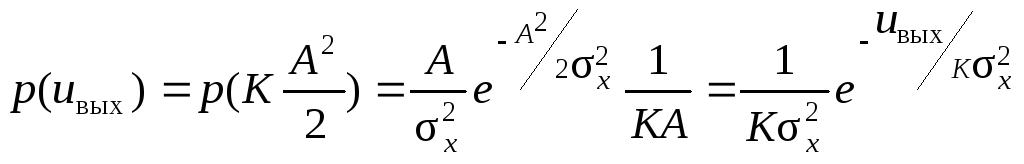т. е. напряжение на выходе квадратичного детектора имеет экспоненциальное распределение.

Математическое ожидание выходного напряжения:

,

средний квадрат напряжения:

.

Отсюда следует, что дисперсия шума на выходе квадратичного детектора:

.

Найдем корреляционную функцию сигнала на выходе: , где.

Энергетический спектр сигнала:

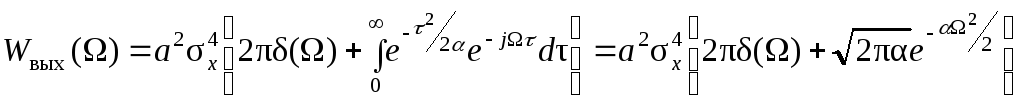.ВЫВОД. Спектры на выходах квадратичного и линейного детекторов одинаковы по форме, отличаются только масштабом оси ординат. Сам сигнал на выходе отличается от сигнала на входе. Это говорит о том, что они воспроизводят спектр огибающей, т. е. то, что необходимо получить.

10.2. Совместное воздействие гармонического сигнала и гауссовского шума на амплитудный и частотный детекторы

Любой сигнал можно преобразовать в гармонический (по теореме Фурье). Поэтому будем рассматривать только гармонический сигнал.

При наложении узкополосного шума на сигнал суммарное колебание можно записать в форме

.

Разложим этот процесс на квадратурные составляющие:

,

где

––

амплитуда,

––

фаза.

Будем рассматривать только амплитуду, так как имеет место амплитудный детектор.

Плотность вероятности огибающей

,

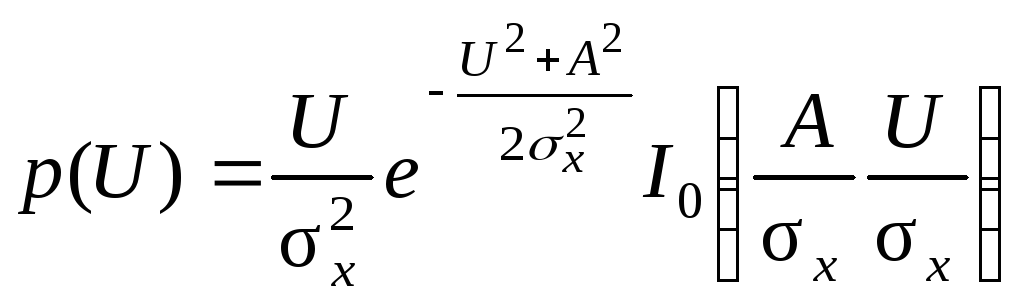где I₀ – бесселева функция нулевого порядка от комплексного аргумента. Это есть обобщенное распределение Релея.

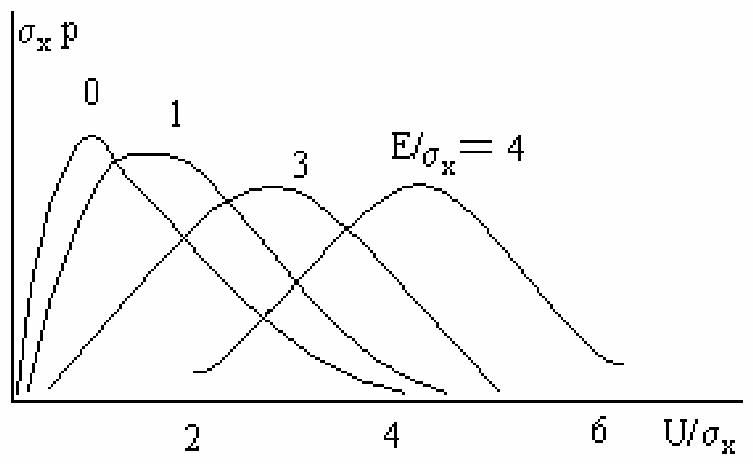
Вид распределения при различных значениях E/_х. При E/_х=0 выражение принимает вид релеевского распределения, при Е>>_х получим распределение, близкое к нормальному, с математическим ожиданием, равным Е, и дисперсией .

Линейный детектор

Пусть напряжение на выходе детектора совпадает с огибающей амплитуды высокочастотного напряжения на входе. Тогда математическое ожидание равно

,

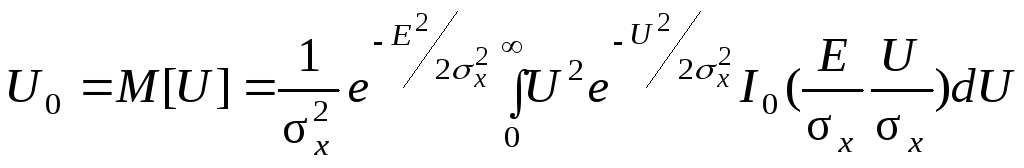а средний квадрат напряжения

.

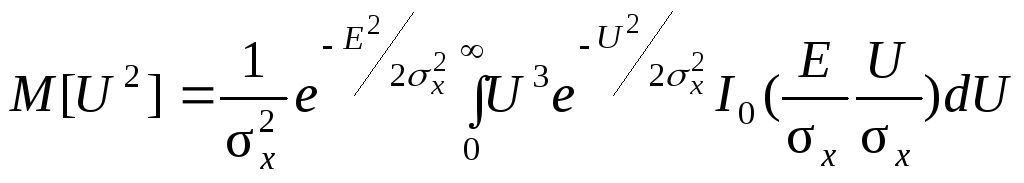После вычисления интегралов получим следующие выражения:

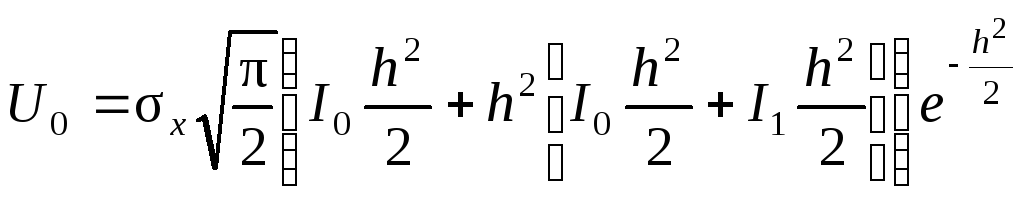, где –– отношение сигнал/шум на входе (отношение мощности полезного сигнала к мощности паразитного сигнала).

Дисперсия сигнала на выходе

.

В отсутствие полезного сигнала математическое ожидание шума распределено по Релею

().

Если есть полезный сигнал на входе, то для получения полезного сигнала на выходе необходимо вычесть шумовую составляющую

().

Следовательно, отношение сигнал/шум на выходе будет .

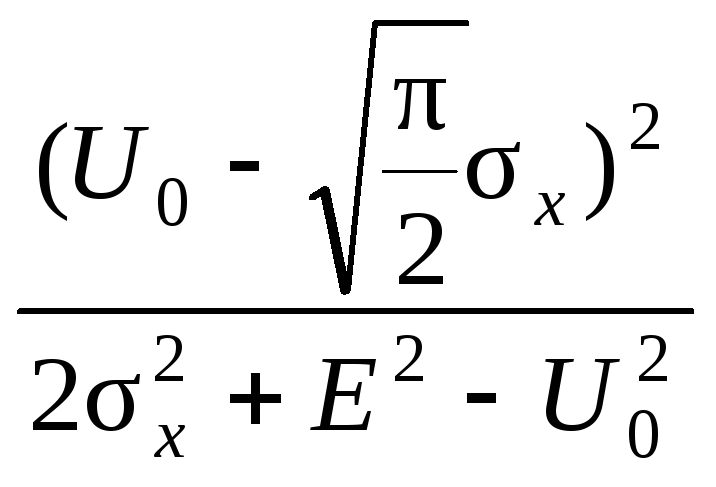Рассмотрим два предельных случая:

1. –– слабый сигнал. В этом случае вводятся упрощения:,.

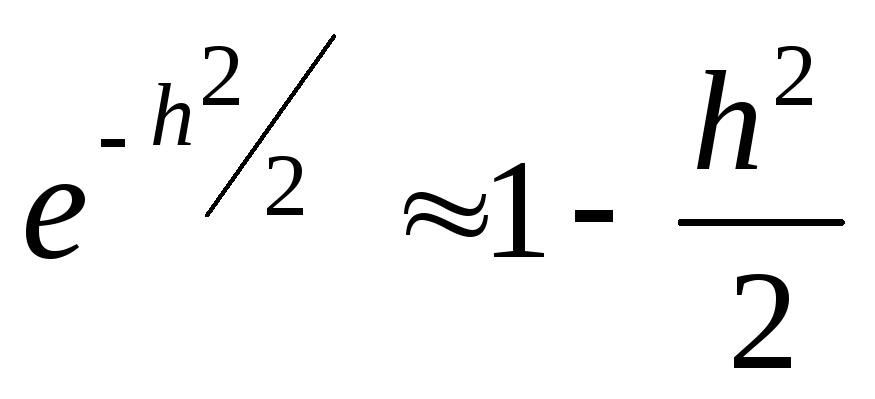Отсюда выражение для U₀ можно записать в укороченном виде: .

Дисперсия:

.

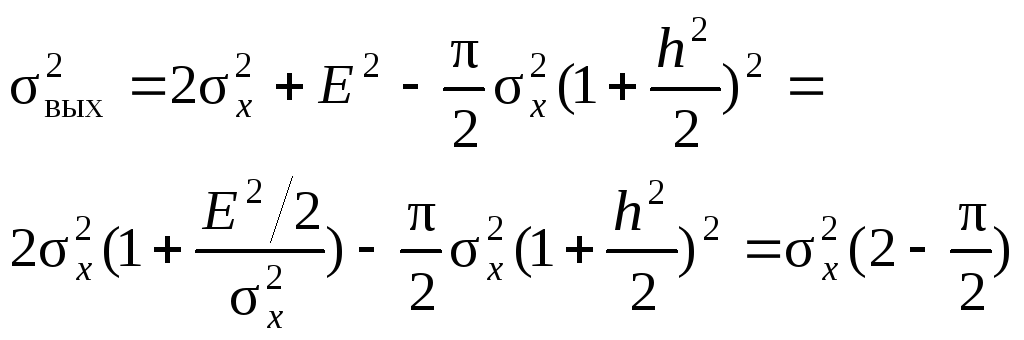При слабом сигнале отношение сигнал/шум на выходе:

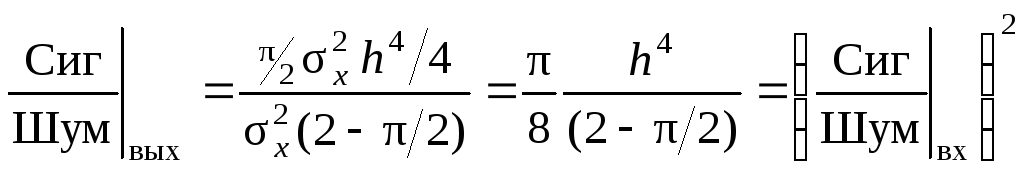
ВЫВОД. Слабый сигнал в линейном детекторе подавляется помехой.

2. –– сильный сигнал. Проведем аналогичный анализ:

, .

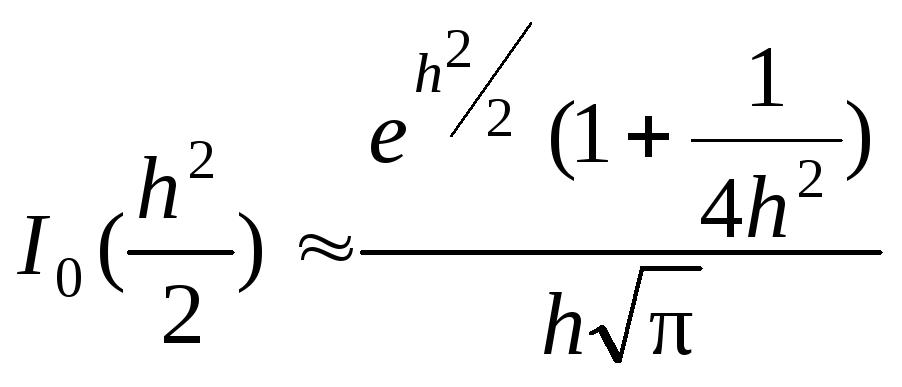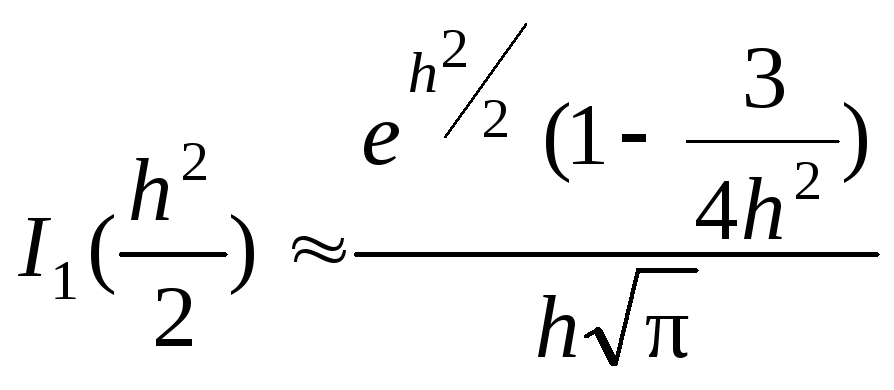U₀ в этом случае принимает вид

,

но

.

Отсюда дисперсия сигнала на выходе

Найдем соотношение сигнал/шум на выходе:

.

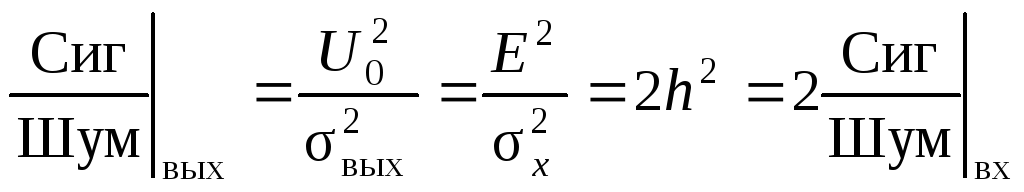ВЫВОД. При сильном сигнале помеха подавляется сигналом.

Квадратичный детектор

Проведем аналогичные рассуждения.

Напряжение на выходе квадратичного детектора

.

Учитывая, что

, и

(так как ), а также

,

получим среднее значение напряжения по времени на выходе: ,

где К – характеристика детектора, Е – амплитуда немодулированного гармонического сигнала, U_ОС – слагаемое, обусловленное помехой, U_ОП – слагаемое, обусловленное сигналом.

Найдем из исходного соотношения:

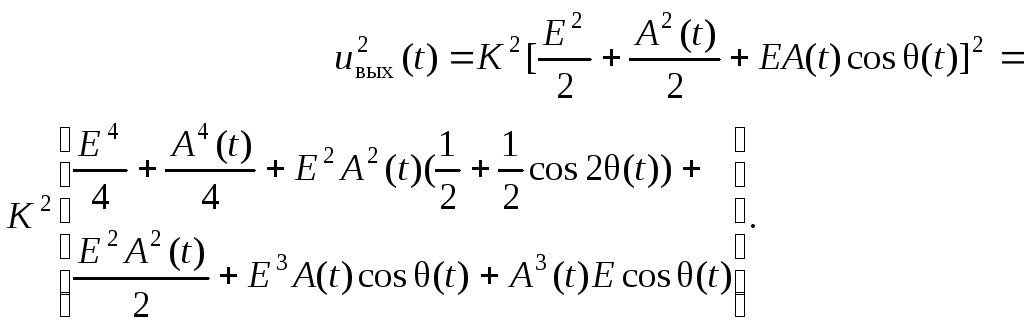
При усреднении по времени все слагаемые с иобращаются в ноль. Следовательно,

.

Вычитая из этого выражения , найдем дисперсию шума на выходе квадратичного детектора:

.

Запишем соотношение сигнал/шум на выходе детектора:

,

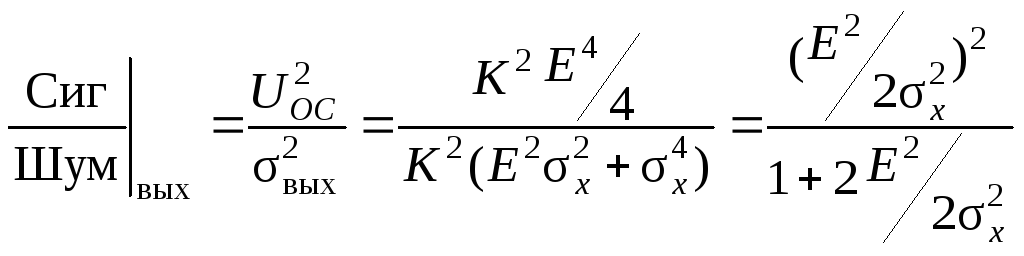где .

При значениях сигнал/шум на входе << 1 (т. е. при )

.

ВЫВОД. При малом отношении сигнал/шум на входе имеет место сильное подавление сигнала.

При значениях сигнал/шум на входе >> 1 (т. е. при )

.

ВЫВОД. При сильном сигнале отношение сигнал/шум на выходе пропорционально отношению сигнал/шум на входе.

Сопоставим результаты для линейного и квадратичного детекторов. При слабом сигнале детекторы ведут себя одинаково: отношение сигнал/шум на выходе пропорционально квадрату отношения сигнал/шум на входе.

При сильном сигнале отношение сигнал/шум на выходе квадратичного детектора в четыре раза меньше, чем у линейного. Это объясняется тем, что при квадратичном детектировании сильный сигнал выносит помеху на участок характеристики с повышенной крутизной, что приводит к относительному увеличению помехи.

Наличие амплитудной модуляции сигнала не вносит существенных изменений в оценку отношения сигнал/шум на выходе детектора. Все результаты не зависят от соотношения между несущей частотой сигнала и мгновенной частотой помехи, т. е. наложение паразитной частотной или фазовой модуляции не оказывает существенного влияния на оценку отношения сигнал/шум на выходе детектора.