
- •Раздел второй Кинематика точки и твердого тела
- •Глава 5. Кинематика точки
- •5.1. Введение в кинематику
- •5.2. Способы задания движения точки
- •5.2.1. Координатный способ задания движения точки
- •5.2.2. Векторный способ задания движения
- •5.2.3. Естественный способ задания движения
- •5.3. Определение скорости точки
- •Векторный способ задания движения точки
- •Координатный способ задания движения
- •5.3.3. Естественный способ задания движения
- •5.4. Определение ускорения точки
- •5.4.1. Векторный способ задания движения
- •5.4.2. Координатный способ задания движения
- •5.4.3. Естественный способ задания движения
- •Глава 6. Поступательное и вращательное движения твердого тела
- •6.1. Поступательное движение твердого тела
- •6.2. Вращательное движение твердого тела
- •6.6. Определение линейных скоростей и ускорений точек вращающегося тела
- •Глава 7. Плоское движение твердого тела
- •7.1. Уравнения плоского движения
- •7.2. Определение скоростей точек тела
- •7.3. Мгновенный центр скоростей.
- •7.4. Определение ускорений точек тела
- •7.5 Мгновенный центр ускорений
- •Глава 8. Сложное движение точки
- •8.1. Относительное, переносное и абсолютное движения
- •8.2. Определение абсолютной скорости
- •8.3. Определение абсолютного ускорения. Теорема Кориолиса
- •Глава 9. Сложное движение твердого тела
- •9.1. Сложение вращательных движений вокруг параллельных осей
- •9.1.1 Вращения направлены в одну сторону
- •9.1.2 Вращения направлены в противоположные стороны
- •9.2. Сложение поступательных движений
- •9.3. Сложение поступательного и вращательного движений
- •9.4. Сложение вращательных движений относительно пересекающихся осей
- •9.5. Сферическое движение тела
- •9.6 Общий случай движения твердого тела
Глава 6. Поступательное и вращательное движения твердого тела
6.1. Поступательное движение твердого тела
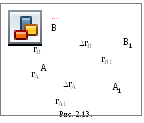
Поступательным называется такое движение твердого тела, при котором любой отрезок прямой, связанный с этим телом, во все время движения остается параллельным самому себе (рис. 2.14). По аналогии с предыдущим найдем:
![]()
![]()
![]()
![]()
Так как по определению,
![]() ,
,
![]()
то
![]() .
.
Переходя к пределу, получим:
![]()
![]()
Очевидно,
![]() ,
,![]() ,
то есть
,
то есть
|
|
(2.20) |
Таким образом при поступательном движении тела все точки его движутся по одинаковым траекториям и в один и тот же момент времени имеют одинаковые скорости и ускорения. Следовательно для поступательного движения твердого тела могут быть использованы все результаты, полученные при изучении движения точки.
6.2. Вращательное движение твердого тела
Вращательным называюттакое движение твердого тела, при котором две какие-нибудь его точки во все время движения остаются неподвижными.
A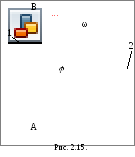 B– ось вращения, 1 – неподвижная плоскость,
2 – подвижная плоскость, жестко связанная
с телом (рис. 2.15).
B– ось вращения, 1 – неподвижная плоскость,
2 – подвижная плоскость, жестко связанная
с телом (рис. 2.15).
Для задания
вращательного движения, надо задать
угол поворота тела как некоторую функцию
времени
![]() (всегда в радианах).
(всегда в радианах).
Основными характеристиками вращательного движения являются угловая скорость и угловое ускорение. Угол поворота меняется с течением времени.
Отношение приращения угла поворота к приращению времени называется средней угловой скоростью.
![]()
![]()
![]()
Истинное значение угловой скорости найдется как предел
|
|
(2.21) |
Таким образом значение угловой скорости в заданный момент времени определяется алгебраической производной от угла поворота по времени.
Для характеристики изменения угловой скорости с течением времени вводится понятие углового ускорения:
|
|
(2.22) |
Среднее угловое ускорение определяется отношением приращения угловой скорости к соответствующему промежутку времени.
Для определения истинного значения углового ускорения необходимо вычислить предел отношения (2.22).
|
|
(2.23) |
У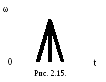 гловая
скорость и угловое ускорение являются
основными характеристиками любой
машины. При пуске
гловая
скорость и угловое ускорение являются
основными характеристиками любой
машины. При пуске![]() и
и![]() увеличивается; в рабочем режиме
увеличивается; в рабочем режиме![]() ,
,![]() ;
после выключения двигателя
;
после выключения двигателя![]() ,
угловая скорость падает до нуля
(рис. 2.16).
,
угловая скорость падает до нуля
(рис. 2.16).
6.6. Определение линейных скоростей и ускорений точек вращающегося тела
Для определения скорости и ускорения какой-нибудь точки Mвращающегося с угловой скоростьюи угловым ускорениемтела воспользуемся естественным способом задания движения. Так как все точки тела движутся по окружностям (рис. 2.17), то закон движения точкиMможно записать в виде
|
|
(2.24) |
П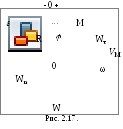 олучив
закон движения точкиM,
найдем ее скорость:
олучив
закон движения точкиM,
найдем ее скорость:
|
или
|
(2.25) |
Таким образом, для определения скорости точки тела необходимо умножить угловую скорость тела на радиус, то есть расстояние точки до оси вращения. Пользуясь уравнениями (2.16)-(2.18), найдем касательное, нормальное и полное ускорения точки M:
|
|
(2.26) |
|
|
(2.27) |
|
|
(2.28) |
Из анализа уравнений (2.25)-(2.28) следует, что скорость и ускорение любой точки вращающегося тела пропорциональны расстоянию этой точки до оси вращения.
Пример 2.8.Для передачи вращения от электродвигателя к смесителю используется плоскоременная передача, при этом на валу двигателя установлен шкив 1 радиусаR1= 0,2 м, а на валу смесителя шкив 2 радиусаR2= 0,4 м (рис. 2.18).
 Определить
угловую скорость
Определить
угловую скорость
![]() и угловое ускорение
и угловое ускорение![]() вала смесителя приt = 2 с,
если известно, что вал двигателя вращается
в соответствии с законом
вала смесителя приt = 2 с,
если известно, что вал двигателя вращается
в соответствии с законом![]() рад.
рад.
Решение.Очевидно, линейные скорости точекAиBшкивов равны (скольжением
ремня и его растяжением пренебрегаем).
Но![]() ,
а
,
а![]() .
Тогда
.
Тогда
![]()
При указанных допущениях касательные ускорения точек AиBтакже равны, но
![]() ,
,
![]() и тогда
и тогда
![]()
Следует заметить, что нормальные ускорения точек AиBне равны. (почему?).
