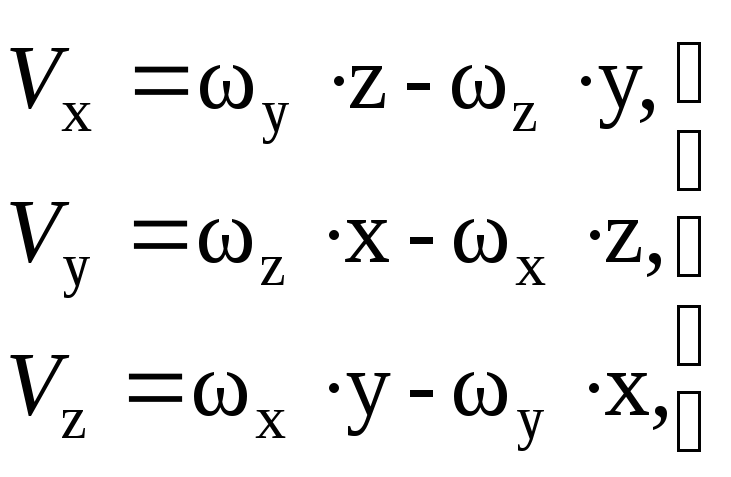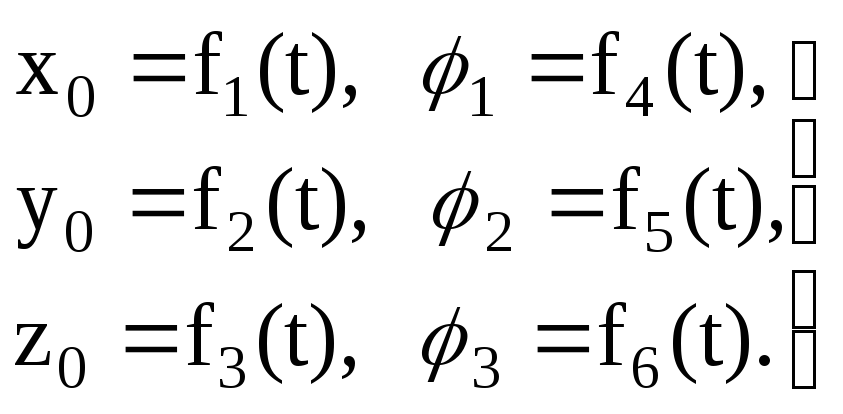9.4. Сложение вращательных движений относительно пересекающихся осей

По аналогии с предыдущим можно утверждать, что результирующее движение будет мгновенно вращательным относительно подвижной оси, совпадающей с вектором мгновенной угловой скорости (рис. 2.41). Величина и направление вектора мгновенной угловой скорости может быть найдена по правилу сложения векторов

.

(2.53)

В данном случае точка О является неподвижной. Такое движение, при котором одна точка тела остается неподвижной, называется сферическим.

9.5. Сферическое движение тела

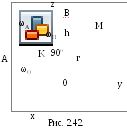
Для удобства назовем вращение тела относительно подвижной оси OAотносительным движением, а вращение вокруг неподвижной осиOB– переносным движением (рис. 2.42). Тогда величина и направление вектора абсолютной мгновенной угловой скорости будет определяться геометрической суммой векторов относительной и переносной угловых скоростей

,

(2.54)

или

Пример 2.15.В планетарном редукторе водило 1 делает 9 об/мин. Определить угловую скорость колеса 2 относительно водила; радиус неподвижного колеса 3 в 1,5 раза больше радиуса колеса 2 (рис. 2.43).

Р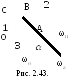ешение.Вектор относительной угловой скорости колеса 2 направлен по оси водилаAB, а переносной по сои 0A. Вектор абсолютной угловой скорости должен проходить через точкуC, в которой подвижное колесо 2 соприкасается с неподвижным колесом 3. Изложенное позволяет построить параллелограмм векторов угловых скоростей на основе (2.54), из которого находим.

Пусть n– число оборотов водила, тогда его угловая скорость. Уголнайдем из соотношения радиусов подвижного и неподвижного колес:.

Окончательно получим:

При решении задач удобнее пользоваться аналитическим методом, спроектировав уравнение (2.54) на оси координат.

Тогда .

(2.55)

Угловое ускорение мгновенного вращения равно векторной производной от абсолютной угловой скорости по времени

	(2.56)
или	(2.57)
			(2.58)

Определение скоростей и ускорений точек тела при сферическом движении

Рассмотрим порядок решения таких задач применительно к произвольной точке М.

Скорость точки Mможно найти как произведение абсолютной угловой скорости на расстояние точки до оси вращения

.

(2.59)

Вектор скорости точки Mперпендикулярен плоскости треугольникаOKMи направлен в сторону абсолютного вращения Если задать положение точкиMрадиусом-вектором, то вектор скорости точкиMможно определить векторным произведением

.

(2.60)

Проецируя (2.60) на оси координат получим:

(2.61)

Для определения ускорения точки необходимо вычислить векторную производную от вектора скорости (2.60):

или

.

(2.62)

Первое слагаемое называется вращательным ускорением, а второе– осестремительным. Тогда

(2.63)

9.6 Общий случай движения твердого тела

Движение тела в общем случае можно рассматривать как сложное, состоящее из поступательного движения вместе с некоторым центром О и сферического движения относительного данного центра. Таким образом уравнения движения тела в общем случае имеют вид:

(2.64)

Скорость любой точки Mможно найти как геометрическую сумму скорости центра О от поступательного движения тела и ее скорости от сферического движения относительно центра О

(2.65)

Заметим, что для равновесия тела в общем случае также необходимо выполнить шесть условий, при этом все уравнения (2.64) не будут зависеть от времени.

83