Введение.

Лекция продолжает изучение темы «Определенный интеграл», включающей в себя четыре лекции, три практических занятия, одно лабораторное занятие. Тема «Определенный интеграл» и данная лекция, в частности, связаны с предыдущей темой «Неопределенный интеграл». Основоположниками интегрального исчисления, по праву следует считать Г. Лейбница, И. Ньютона. В 19 веке Г. Риман (1826-1866) создал теорию интеграла, обобщающую результаты, полученные О. Коши. Приложениями определенного интеграла занимались И. Кеплер (1571-1630) в своих исследованиях по астрономии, Б. Кавальери (1598-1647) и Э. Торричелли (1608-1647). Ответы на многие вопросы, связанные с существованием площадей и объемов фигур были получены К. Жорданов (1838-1922). В дальнейшем обобщения понятия интеграла были предложены французскими математиками А. Лебегом (1875-1941) и А. Данжуа (1884-1974), советским математиком А. Хинчиным(1894-1959). Лекция тесно связана с тематикой последующих и предыдущих тем.

1.Вычисление площадей плоских фигур.

Как известно, площадь криволинейной трапеции, ограниченной непрерывной линией и прямыминаходится по формуле

, (1)

где .

Если , то определенный интеграл (1) неположителен. Его абсолютная величина равна площади криволинейной трапеции, расположенной ниже осиOx, т.е. .

Если же функция f(x) меняет на отрезке знак конечное число раз, то для вычисления площади фигуры можно разбить отрезок интегрирования на части, гдеf(x) не меняет знака, а затем найти по формуле (1) площади фигур, полученных таким образом и взять их алгебраическую сумму.

Пример 1. Найти площадь фигуры, ограниченной косинусоидой и прямыми

Решение. Разобьем отрезок на такие части, где функциясохраняет постоянный знак. Посколькуприипри, имеем

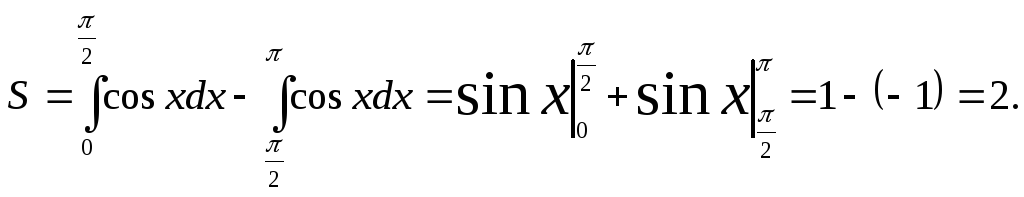
S

a b x a c b x

Рис 1. Рис.2

Найдем площадь фигуры, заключенной между двумя кривыми (рис.1). Пусть для определенности. Тогда площадьS равна разности площадей криволинейных трапеций, ограниченных сверху соответственно графиками функций , т.е.

. (2)

Если графики функций пересекаются на отрезке конечное число раз (рис.2), то отрезок интегрирования нужно разбить на такие части, где разность сохраняет постоянный знак, и найти площади полученных частей по формуле (2).

Вычисление площади криволинейной трапеции для кривой, заданной параметрически.

Пусть кривая задана параметрическими уравнениями

(3)

где функция непрерывна, анепрерывно дифференцируема. Пусть, далее, уравнения (3) определяют интегрируемую функциюy=f(x) на отрезке, так, что различнымсоответствуют различные точки кривойy=f(x), которая сама себя не пересекает, причемплощадь криволинейной трапеции определяется по формуле (1). Выполним в формуле (1) подстановку; имеемЕсли; если. Тогда формула (1) примет вид

(4)

Пример 2. Найти площадь фигуры, ограниченной эллипсом.

Решение. Параметрические уравнения эллипса имеют вид . В силу симметрии эллипса достаточно найти площадьодной его четверти, а затем умножить результат на 4. Еслиxизменяется в

пределах , то параметрtизменяется. По формуле (4) получим

Вычисление площадей в полярных координатах.Пусть в полярной системе координат задана функция, где- полярный радиус,- полярный угол. Пусть, далее, функциянепрерывна при изменении углав пределах. Фигура, ограниченная частьюABграфика функциии прямыми, соединяющими полюсOс точкамиAиB, называется криволинейным сектором.

B

(рис.3)

Вычислим площадь криволинейного сектора OAB. Разобьем уголнаnчастей лучами, соответствующими значениям полярного угла. Обозначим углы между проведенными лучами через. Дляk-го угла имеем. Ясно, что площадь криволинейного сектораOABравна суммеnмалых площадей, его составляющих. Рассмотри криволинейный сектор. Выберем некоторый угол, удовлетворяющий неравенствам, и обозначим длину соответствующего этому углу радиуса через. Заменим площадьk-го криволинейного сектора площадью кругового сектора с радиусоми центральным углом. Его площадь равна. Так как, то площадьk-го кругового сектора вычисляется по формуле. Сумма площадейnкруговых секторов составит

(5)

Сумма является интегральной суммой Римана для функциина отрезке. Переходя в равенстве (5) к пределу при, получим

. (6)

В равенстве (6) левая часть есть площадь Sкриволинейного сектораOAB, а правая часть равна определенному интегралу. Таким образом, соотношение (6) примет вид

. (7)

Пример 3. Найти площадь круга радиуса R.

Решение. Уравнение окружности в полярных координатах имеет вид . В силу симметрии круга достаточно вычислить площадьчетверти круга, а затем умножить результат на 4. Полярный угол, соответствующий площадиизменяется в пределах. По формуле (7) находим

что согласуется с общеизвестной формулой.