
- •Лекция 1
- •Классификация нагрузок
- •Основные гипотезы
- •2. Упругие свойства материала во всех направлениях одинаковы, т. Е. Материал тела обладает упругой изотропией.
- •3. Тело считается абсолютно упругим.
- •4. Деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в этой точке (закон Гука).
- •2. Метод сечений
- •Метод сечений
- •3. Напряжения и деформации
- •4. Условия прочности.
- •5.Типы задач сопротивления материалов
- •Вопросы для контроля знаний
- •Лекция 2
- •1 Участок:
- •2 Участок:
- •3 Участок:
- •2. Напряжения и расчет стержней на прочность
- •2. Подбора поперечного сечения (известны и ):
- •3. Определения грузоподъемности (известны и ):
- •3. Деформации и перемещения при
- •Базовые вопросы
- •I Условные обозначения и основные математические зависимости
- •II. Последовательность построения эпюр и выполнение расчетов
- •III Решение задач
III Решение задач
Задача 1. Для бруса, изображенного на рис. 1, а, построить эпюры внутренних сил, напряжений и перемещений по длине бруса.
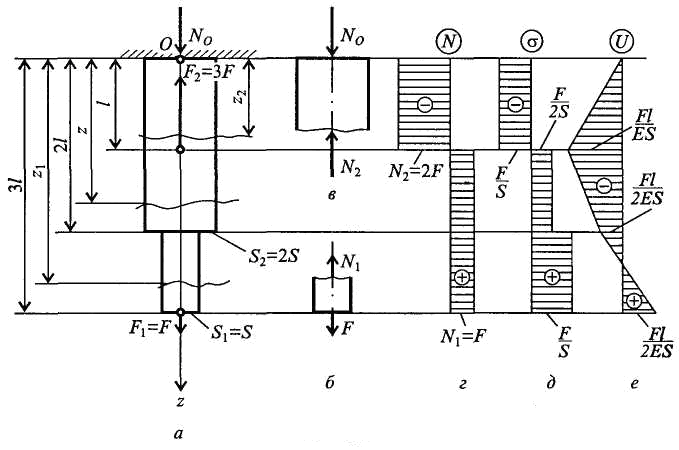
Рис. 1
Решение.
1. Выбираем начало отсчета в неподвижном сечении (точка О); положительное направление оси z направим по оси бруса, т.е. вниз.
2. Определим реакцию, составив одно уравнение равновесия:
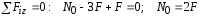 .
.
3. Построим эпюру внутренних сил N. Для этого на расстоянии z1 рассечем брус и рассмотрим равновесие нижней части (рис. 1, б):
 ,
,
что
справедливо для
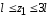 .
В этих пределах в брусе возникает
растяжение, так какN1
направлена от сечения.
.
В этих пределах в брусе возникает
растяжение, так какN1
направлена от сечения.
Теперь
выберем второй участок бруса
 и рассмотрим равновесие верхней части
(рис. 1,в):
и рассмотрим равновесие верхней части
(рис. 1,в):
 .
.
Поскольку N2 направлена к сечению, то брус под действием сил N0 и N2 сжимается.
После того как определили все внутренние нормальные силы, переходим к построению эпюры нормальных сил (рис. 1, г). Вправо будем откладывать положительные значения, а влево - отрицательные значения нормальных сил.
Анализируя построенную эпюру N, заметим, что внутренние силы не зависят от размеров поперечного сечения, а зависят только от приложенных внешних сил. Поэтому длину бруса разбивают на такое число участков, сколько сил на его длине приложено. В данном случае было два участка.
При проверке правильности построения эпюры N следует обратить внимание на то, что на эпюре внутренних сил в тех сечениях, где были приложены внешние силы, должны быть скачки, равные приложенной внешней силе.
4. Построим эпюру напряжений σ. Брус следует разбить на участки. Поскольку σ = N/S, то участков на эпюре будет столько, сколько раз меняется поперечное сечение; при этом следует обращать внимание, чтобы при постоянной площади поперечного сечения нормальная сила на эпюре N оставалась неизменной. С учетом этого на эпюре σ будут три различных значения σ (рис. 1, д):
 .
.
5. Строим эпюру перемещений U. Начинать следует от неподвижного сечения, т.е. от сечения О. Выразим перемещение сечения, находящегося от неподвижного на расстоянии z2:
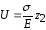 .
.
Если
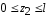 ,
то дляz2
=l
перемещение
,
то дляz2
=l
перемещение

Для

 ,
,
или
 ;
;
при z = 2l
 .
.
Для
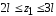
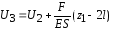 ;
;
при z1=3l
 .
.
Откладываем вычисленные перемещения на эпюре U (рис. 1, е).
Определить диаметры поперечных сечений бруса (материал - незакаленная сталь 30), нагруженного по схеме, приведенной на рис. 1, а. Сила F=1000 Н.
Сначала необходимо построить эпюры N и σ. Определяем коэффициент запаса. Поскольку материал пластичный, принимаем коэффициент запаса nT = 1,5.
Вычисляем допускаемое напряжение. Из табл. 2.1 для стали 30 выписываем σтр = σmc = 330 Н/мм2. После этого можно определить допускаемое напряжение при растяжении и сжатии:
 Н/мм2.
Н/мм2.
Проанализировав эпюру напряжений (рис. 1, д), установили, что на двух участках возникает одинаковое напряжение σнаи6 = F/S. Поскольку данный материал работает одинаково на растяжение и сжатие, то можно для любого из этих двух участков записать условие σнаи6≤ [σ]:
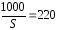 .
.
Определяем диаметры круглого бруса из полученного уравнения: S = 4,55 мм2. Зная, что S = πr2, определяем r1 = 1,2 мм; d1 = 2,4 мм. На участке, где площадь S2 = 2S, диаметр d2 будет равен 3,35 мм.
Задача 2. Построить эпюру продольных сил для стержня, нагруженного продольными силами (рис. 2.1, а).
Решение. Стержень имеет два участка: I и II. Выберем начало координат в левом крайнем сечении.

Рис. 2.1. Определение продольных сил на участках I и II
Найдем закономерности изменения продольной силы на каждом участке. Для этого используем метод сечений — в произвольных местах на участках I и II проведем сечения 1—1 и 2—2 и каждый раз будем отбрасывать правую часть стержня, содержащую закрепление, для того чтобы предварительно не определять опорную реакцию. Оставшиеся левые части уравновесим положительными (растягивающими) продольными силами N1 и N2 (рис. 2.1, б, а).
Заметим, что во избежание ошибки следует неизвестное внутреннее усилие принимать всегда положительным, так как знак усилия, получаемый из решения, позволит установить:
правилен ли был выбор направления силы N;
какой вид деформации при этом возникает — растяжение или сжатие.
Для оставшихся (левых) частей запишем уравнения равновесия:
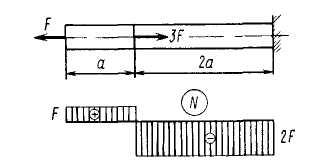
Рис. 2.2. Построение эпюры продольных сил
I.
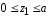 :
:

II.
 :
:
 .
.
Из полученного решения видно, что в пределах каждого участка продольная сила остается постоянной, т. е. не зависит от продольной координаты z, и на участке II вместо предполагаемой растягивающей силы продольная сила будет сжимающей (рис. 2.1, в она показана пунктиром).
По полученным выражениям для N1 и N2 построим эпюру продольных сил, изображенную на рис. 2.2.
Задача
3. Построить
эпюру
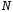 (рис. 3).
(рис. 3).

Рис. 3
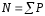 справа
справа
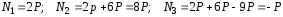 .
.
Задача
4. Построить
эпюру
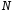 (рис. 4).
(рис. 4).
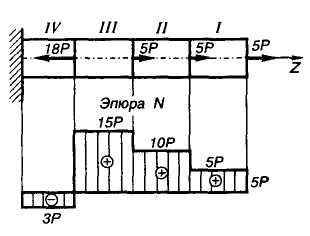
Рис. 4

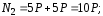
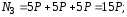
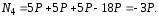
Задача
5. Построить
эпюру
 (рис. 5).
(рис. 5).
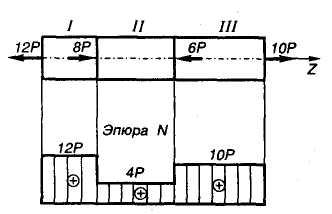
Рис. 5
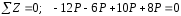 .
.
Здесь
«Идем» справа:



«Идем» слева:


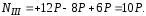
Задача
6. Для
стального бруса (рис. 6) постройте эпюру
продольных
сил, эпюру напряжений, проверьте
прочность, если:
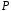 =50
кН,
=50
кН,
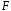 =10см2,
=10см2,
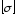 = 160МПа.
= 160МПа.
Решение. По эпюре напряжений выбираем максимальное напряжение и записываем условие прочности:
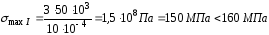 ;
;
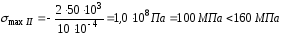 ;
;
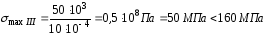
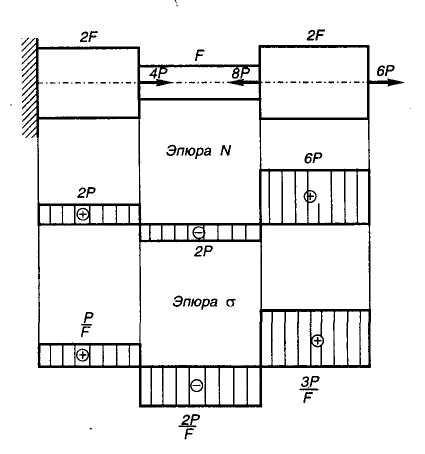
Рис. 6
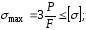
Условие прочности выполняется; прочность бруса обеспечена.
Задача
7.
Построим эпюру N
для стержня, изображенного на рис. 7, а.
Установим с помощью метода сечений
законы изменения N
в пределах каждого из двух характерных
участков стержня. Для этого проведем
сечения в пределах этих участков,
отбросим мысленно одну из частей стержня
и заменим ее влияние продольной силой
N.
Составим уравнение равновесия ΣХ=
0 оставшейся части.




Участок
х≥1,2
м
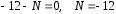 кH.
кH.
Истинное направление N показано пунктиром (рис. 7, б). В пределах рассматриваемого участка продольная сила является сжимающей и имеет постоянное значение.
Участок 0≤ х ≤< 1,2 м
 .
.

Рис. 7
Определим величину N в начале и в конце участка (рис. 7, в):
х = 0, N=-18 кН (сжатие);
х=1,2м, N = 6 кН (растяжение).
В пределах данного участка продольная сила изменяется по линейному закону. Опорная реакция в месте закрепления стержня равна значению N в этом сечении: R = 18 кН.
Отложив в соответствующем масштабе ординаты N на прямой, параллельной оси стержня, построим эпюру N (рис. 7, г). Отметим ее особенность — в сечении, где приложена сосредоточенная сила P1 = 18 кН, на эпюре N имеется разрыв (скачок), равный по величине этой силе.

