
- •Лекция 1
- •Классификация нагрузок
- •Основные гипотезы
- •2. Упругие свойства материала во всех направлениях одинаковы, т. Е. Материал тела обладает упругой изотропией.
- •3. Тело считается абсолютно упругим.
- •4. Деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в этой точке (закон Гука).
- •2. Метод сечений
- •Метод сечений
- •3. Напряжения и деформации
- •4. Условия прочности.
- •5.Типы задач сопротивления материалов
- •Вопросы для контроля знаний
- •Лекция 2
- •1 Участок:
- •2 Участок:
- •3 Участок:
- •2. Напряжения и расчет стержней на прочность
- •2. Подбора поперечного сечения (известны и ):
- •3. Определения грузоподъемности (известны и ):
- •3. Деформации и перемещения при
- •Базовые вопросы
- •I Условные обозначения и основные математические зависимости
- •II. Последовательность построения эпюр и выполнение расчетов
- •III Решение задач
1 Участок:
 .
.

Рис. 3.2
2 Участок:
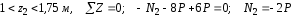 .
.
(направление
 — в обратную
сторону).
— в обратную
сторону).
3 Участок:
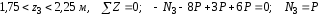 .
.
Приведенные
уравнения статики
показывают, что продольная сила
 ,
действующая
в каком-то сечении, является
равнодействующей
всех внешних сил, действующих по одну
сторону проведенного
сечения:
,
действующая
в каком-то сечении, является
равнодействующей
всех внешних сил, действующих по одну
сторону проведенного
сечения:
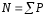 с
одной стороны. (3.1)
с
одной стороны. (3.1)
Скачок
на эпюре
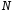 равен
приложенной в
этом сечении сосредоточенной силе.
равен
приложенной в
этом сечении сосредоточенной силе.
В
сечении А
(рис. 3.2)
(заделка) есть реакция
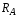 ,
которую
можно найти из
,
которую
можно найти из
 .
.
2. Напряжения и расчет стержней на прочность
При центральном растяжении (сжатии) в поперечном сечении возникают нормальные напряжения:
 ,
,
где
 —
продольная сила;
—
продольная сила;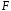 - площадь поперечного сечения.
- площадь поперечного сечения.
Эти напряжения распределены по поперечному сечению равномерно (рис. 3.3).

Рис. 3.3
Пример
1. Построить
эпюру продольной силы
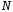 (в долях
(в долях
 )
и эпюру напряжений
)
и эпюру напряжений (в долях
(в долях
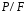 — рис. 3.4,
а).
— рис. 3.4,
а).
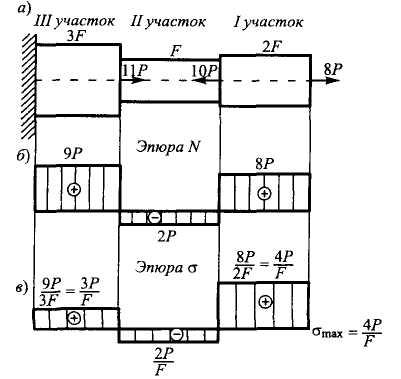
Рис. 3.4
Решение.
Строим эпюру
 (рис. 3.4, б)
(рис. 3.4, б)
1
участок:
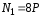 .
.
2
участок:
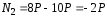 .
.
3
участок:
 .
Строим
эпюру напряжений
.
Строим
эпюру напряжений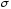 (рис. 3.4,в)
(рис. 3.4,в)
1
участок:
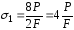 .
.
2
участок:
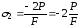 .
.
3
участок:
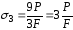 .
.
Расчет на прочность конструкций из пластичного материала отличается от расчета на прочность конструкций из хрупкого материала.
Для
конструкции из пластичного
материала
допускаемое
напряжение
 на
растяжение
и сжатие одинаково.
на
растяжение
и сжатие одинаково.
Условие прочности:
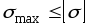 ,
(3.2)
,
(3.2)
где
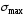 —
наибольшее поабсолютной
величине напряжение.
—
наибольшее поабсолютной
величине напряжение.
Хрупкий материал значительно хуже работает на растяжение, чем на сжатие:
 ,
,
где
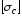 — допускаемое напряжение на сжатие;
— допускаемое напряжение на сжатие;
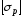 — допускаемое напряжение на растяжение.
— допускаемое напряжение на растяжение.
Условие прочности для хрупкого материала:
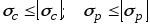 ,
(3.3)
,
(3.3)
где
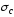 и
и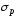 — наибольшие расчетные сжимающие и
растягивающиенапряжения.
— наибольшие расчетные сжимающие и
растягивающиенапряжения.
Условие прочности
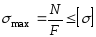
может быть использовано для:
Проверочного расчета напряжений (известны
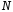 и
и
 ):
):
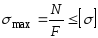
2. Подбора поперечного сечения (известны и ):
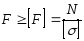 .
.
3. Определения грузоподъемности (известны и ):
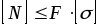 .
.
По
полученному значению
 ,
используя
эпюру продольных сил, определяем
допустимую внешнюю нагрузку
,
используя
эпюру продольных сил, определяем
допустимую внешнюю нагрузку
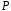 .
.
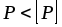 ,
,
где
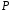 — действующая
внешняя нагрузка.
— действующая
внешняя нагрузка.
3. Деформации и перемещения при
РАСТЯЖЕНИИ — СЖАТИИ
При растяжении и сжатии бруса меняются его продольные и
поперечные размеры (рис. 3.5).
При растяжении длина бруса меняется на:
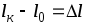 ,
,
а ширина бруса меняется на:
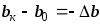 .
.
При сжатии:
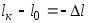 ,
,
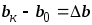
где
 — абсолютная продольная деформация
(см,
м);
— абсолютная продольная деформация
(см,
м);
 — абсолютная
поперечная деформация
(см,
м).
— абсолютная
поперечная деформация
(см,
м).
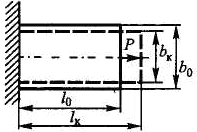
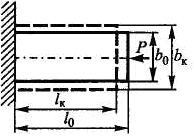
Рис. 3.5
Перейдем к относительным деформациям (безразмерным):
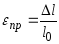 - относительная
продольная деформация;
- относительная
продольная деформация;
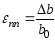 - относительная
поперечная деформация.
- относительная
поперечная деформация.
При растяжении бруса
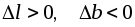 ;
;
при сжатии
 ,
,
т.
е. и при растяжении, и при сжатии
 и
и
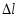 ,
а следовательно,
,
а следовательно,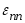 и
и
 имеют разные знаки, поэтому отношение
этих величин (всегда отрицательное)
берется по абсолютной величине.
имеют разные знаки, поэтому отношение
этих величин (всегда отрицательное)
берется по абсолютной величине.
Коэффициент поперечной деформации, или коэффициент Пуассона (табл. 3.1):
 .
(3.4)
.
(3.4)
Таблица 3.1
|
Материал |
|
|
Сталь легированная Чугун серый |
0,25 – 0,3 0,23 — 0,27 |
Закон Гука выражает прямо пропорциональную зависимость между нормальным напряжением и относительной деформацией:
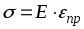 .
(3.5)
.
(3.5)
Закона Гука можно представить в другом виде:
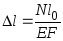 .
(3.6)
.
(3.6)
Из последнего выражения легко получить выражение (3.5):
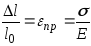 ,
,
где E—модуль продольной упругости (физическая постоянная материала, характеризующая его способность сопротивляться упругому деформированию, табл. 2);
EF—жесткость поперечного сечения бруса при растяжении — сжатии.
Таблица 3.2
|
Материал |
|
|
Сталь легированная Чугун серый Стекло Медь прокатная Алюминиевая проволока |
(2,1 — 2,2) • 105 (1,15 —1,6) • 105 0,56 105 1,10 105 0,70 105 |
Деформация бруса (растяжение или сжатие) вызывает перемещение поперечных сечений. На рис. 3.6 показан брус, каждое волокно которого удлиняется на величину
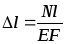 -
(здесь
-
(здесь
 ),
),
а
сечение
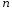 —
—
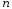 перемещается
в положение
перемещается
в положение
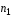 —
—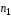 на
величину
на
величину
 .
.

Рис. 3.6 Рис. 3.7
В этом случае:
 .
.
Рассмотрим
брус, показанный на рис. 3.7. Левый участок
бруса деформируется и сечение
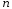 —
—
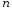 перемещается в положение
перемещается в положение
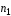 —
—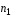 на
величину
на
величину
 ;
правый участок недеформируется
(нет продольной силы) и каждое его сечение
оказывается
перемещенным на эту же величину
;
правый участок недеформируется
(нет продольной силы) и каждое его сечение
оказывается
перемещенным на эту же величину
 .
Сечениет
—
т
переместится
на столько же, насколько переместилось
сечение
.
Сечениет
—
т
переместится
на столько же, насколько переместилось
сечение
 —
—
 :
:
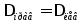 .
.
Рассмотрим
случай, когда продольная сила есть на
обоих участках
рассматриваемого бруса (рис. 3.8).
Перемещение сечения т
—
т
(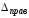 )
(правое сечение) зависит от перемещения
сечения
)
(правое сечение) зависит от перемещения
сечения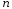 —
—
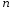 (
( )
и перемещения сечения т
—
т
относительно
сечения п
— п (
)
и перемещения сечения т
—
т
относительно
сечения п
— п ( ):
):
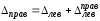 ,
,
где
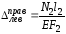 .
.
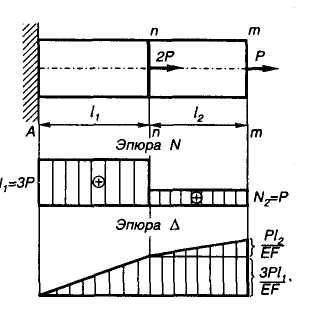
Рис. 3.8
Для рассматриваемого примера (EF= const):
 ;
;
 .
.
Перемещение
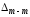 можно получить, используя не внутренние
усилия
можно получить, используя не внутренние
усилия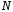 ,
а
внешние силы. Рассуждаем так: сила
,
а
внешние силы. Рассуждаем так: сила
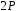 растягивает
только
участок длиной
растягивает
только
участок длиной
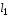 сила
сила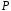 растягивает
весь брус длиной
растягивает
весь брус длиной
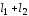 :
:
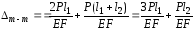 .
.
Используя
полученные значения, построим эпюру
перемещений (рис.
3.8). Учитываем, что в заделке перемещение
равно нулю (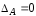 ).
).
При
перемещении бруса от действия
собственного
веса
(рис. 3.9), считая вес груза сосредоточенным
в середине длины
 ,
получим
,
получим
 ,
,
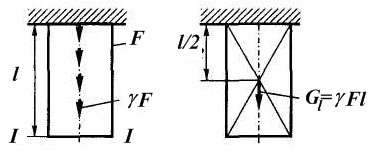
Рис. 3.9
где
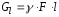 —
вес бруса длиной
—
вес бруса длиной
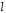 ;
;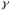 —
удельный вес материала.
—
удельный вес материала.

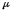
 ,
МПа
,
МПа