
- •Сопротивление материалов Задача 1. Расчет стержней при центральном растяжении ( сжатии).
- •3.4.1. Практические рекомендации для расчета
- •II.Построение эпюр поперечных сил и изгибающих моментов
- •III. Подбор сечения балки
- •II.Построение эпюр поперечных сил (рис.14.Г)
- •III.Построение эпюр изгибающих моментов (рис.14.Д)
- •III. Подбор сечения балки
- •1. Круглое сечение
III.Построение эпюр изгибающих моментов (рис.14.Д)
На участке I изгибающий момент изменяется по линейному закону.
 .
.
Знак минус перед силой F поставлен по той причине, что левая часть балки на этом участке от силы F изгибается выпуклостью вверх, т.е. сжатые волокна балки находятся снизу.
При

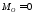 ,
,
при
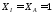 м
м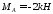 м.
м.
На участке II эпюра момента также имеет линейный вид:
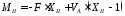 .
.
Здесь
сила VA
приложена к балке снизу, поэтому от нее
балка изгибается выпуклостью вниз, т.е.
сжатые волокна расположены сверху.
Плечо момента от силы VA
до рассматриваемого сечения с координатой
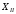 равно
равно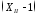 ,
т.к. оно короче плеча до силыF
на 1м.
,
т.к. оно короче плеча до силыF
на 1м.
Подставляем крайние значения текущей координаты.
При
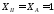 м
м ,
,
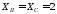 м
м
 .
.
На
участке III для сечения с координатой
 начинает действовать распределенная
нагрузка, что является причиной для
изменения характера эпюры момента; она
становится квадратичной параболой.
начинает действовать распределенная
нагрузка, что является причиной для
изменения характера эпюры момента; она
становится квадратичной параболой.
 .
.
В
этом выражении составляющая изгибающего
момента от распределенной нагрузки
имеет 3 сомножителя. Второй сомножитель
 является расстоянием от сечения с
координатой
является расстоянием от сечения с
координатой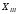 до сечения, где начинает действовать
распределенная нагрузка, т.е. до точки
до сечения, где начинает действовать
распределенная нагрузка, т.е. до точки .
Суммарное воздействие на балку от
распределенной нагрузки, равное
.
Суммарное воздействие на балку от
распределенной нагрузки, равное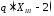 ,
эквивалентно сосредоточенной нагрузке
того же значения, но приложенной точно
посередине этого участка. По этой причине
плечо эквивалента распределенной
нагрузки до рассматриваемого сечения
всегда вдвое короче длины нагруженного
распределенной нагрузкой участка, а
именно:
,
эквивалентно сосредоточенной нагрузке
того же значения, но приложенной точно
посередине этого участка. По этой причине
плечо эквивалента распределенной
нагрузки до рассматриваемого сечения
всегда вдвое короче длины нагруженного
распределенной нагрузкой участка, а
именно: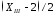 .
.
Следует обратить внимание, что в точке С приложен сосредоточенный момент, что вызывает соответствующий скачок изгибающего момента на эпюре. Сосредоточенный момент берется со знаком минус, т.к. он гнет левую часть балки выпуклостью вверх (сжатые волокна снизу).
При
 м
м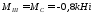 ,
,
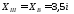
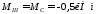 .
.
Найдем
вершину квадратичной параболы, т.е.
экстремальное значение изгибающего
момента в той координате
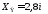 ,
которой соответствует нулевое значение
QIII.
,
которой соответствует нулевое значение
QIII.
 .
.
Для IV участка изгибающий момент имеет следующий вид
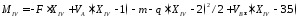 .
.
По крайним значениям строим эпюру, которая также имеет вид квадратичной параболы, выпуклой частью обращенной навстречу распределенной нагрузке.
При
 м
м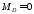 .
.
Примечание к данному пункту.
Построение эпюр Q и М на IV участке можно осуществить и на основе других выражений, что может одновременно послужить и способом самоконтроля для проверки правильности вычисления Q и М.
Значения
Q для этого участка удобнее определять,
рассматривая правую отсеченную часть
балки. В этом случае начало координат
размещается на правом конце балки, а
ось Х - в противоположном направлении
вдоль оси балки, т.е.
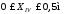 .
Это позволяет существенно упростить
выражение для QIV
, а именно:
.
Это позволяет существенно упростить
выражение для QIV
, а именно:
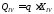 .
.
При
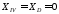 QD
= 0,
QD
= 0,
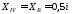 QB
=2кН.
QB
=2кН.
Результат, как видим, полностью совпадает с предыдущими вычислениями.
По аналогии изгибающий момент на IV участке
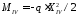 .
.
При
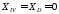
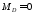 ,
,
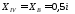
 .
.
Оценивая построенные эпюры Q и М с точки зрения правил п.3.4.2 можно сделать заключение, что обе они соответствуют приведенным там критериям проверки.
III. Подбор сечения балки
Опасным
является сечение в точке А, где действует
максимальный по абсолютному значению
изгибающий момент
 .
.
Условие
прочности для балки из пластичного
материала
 .
.
