4.Дифференциальные уравнения плоского движения твердого тела.

Дифференциальные уравнения плоскопараллельного дви­жения твердого тела представляют собой совокупность уравне­ний поступательного движения плоской фигуры вместе с цен­тром масс и вращательного движения относительно оси, прохо­дящей через центр масс:

,

,

.

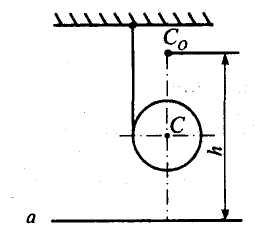
Задача 3. Однородный круглый цилиндр массы М обмотан посредине тонкой нитью, конец В которой закреплен неподвижно. Ци­линдр падает без начальной скорости, разматывая нить. Опре­делить скорость оси цилиндра, после того как он опустится на высоту h, и найти натяжение нити .

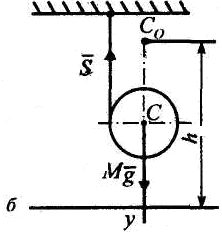
Решение. Изобразим цилиндр в произвольном положении. Покажем силы: вес и силунатяжения нити . Запишем дифференциальные уравнения плоскопараллельного движения:

;

.

Заменим и умножим первое уравнение наR, а затем его сложим со вторым. Получим

.

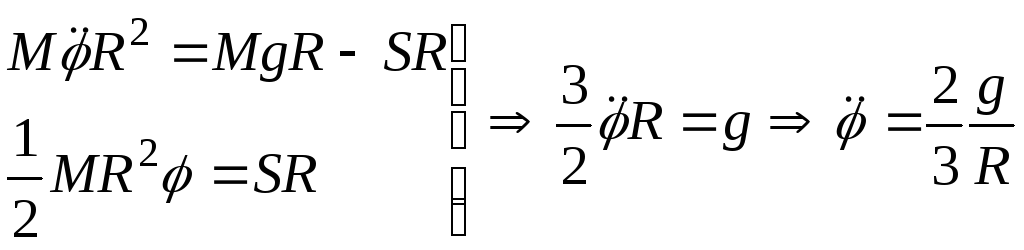Заменим .

После интегрирования получим

.

Так как , то.

Натяжение нити

.

Задача 4. Шкив массой т = 90 кг и радиусом r = 30 см враща­ется с угловой скоростью ω = 20 с^–1. Для его остановки на шкив оказывается действие через невесомый ремень, натяжения ветвей которого равны Т₁= 40 Н и Т₂ = 20 Н (рис. 55). Радиус инерции шкива ρ = 20 см. Определить время торможения шкива t₁ и угол φ₁, на который он повернется за это время.

Рис. 55 Рис. 56

Решение. Рассмотрим все силы, действующие на шкив и прилежащую к нему часть ремня: силы натяжения вет­вей ремня Т₁ и Т₂ , силу тяжести шкива G, составляющие реакции в подшипниках Х₀ и У₀ (рис. 56). Применим к шкиву дифференциальное уравнение вращательного движения относительного его оси z

.

Здесь кгм² — осевой момент инер­ции шкива. Стоящий в правой час­ти уравнения главный момент вне­шних сил относительно оси враще­ния обозначим для краткости . Он будет в данном случае равен Нм, по­скольку силы G, Х₀ и У₀ имеют ну­левые моменты относительно оси z (моменты сил, действующих по дви­жению, должны браться со знаком «плюс», а против движения — со знаком «минус»).

Таким образом, дифференциальное уравнение враща­тельного движения имеет вид

Для интегрирования этого уравнения делим переменные, учитывая что =const и J_z = const

, (*)

после чего в левой и правой частях ставим интегралы.

После интегрирования , по­лучим

,

oткуда

,

где постоянная интегрирования C₁ может быть найдена из начального условия ω = ω₀ при t = 0. Подставив в уравне­ние эти значения, получим J_z, и тогда J_z, откуда

.

Используя последнее соотношение, можно найти вре­мя торможения шкива, т. е. время t_l за которое угловая скорость обратится в ноль

и тогда

Для определения угла поворота φ, заменив в уравнении для угловой скорости ω=dφ/dt, получим

Деля здесь переменные и интегрируя с использованием определенных интегралов (учиты­вая, что φ = 0 при t = 0), находим

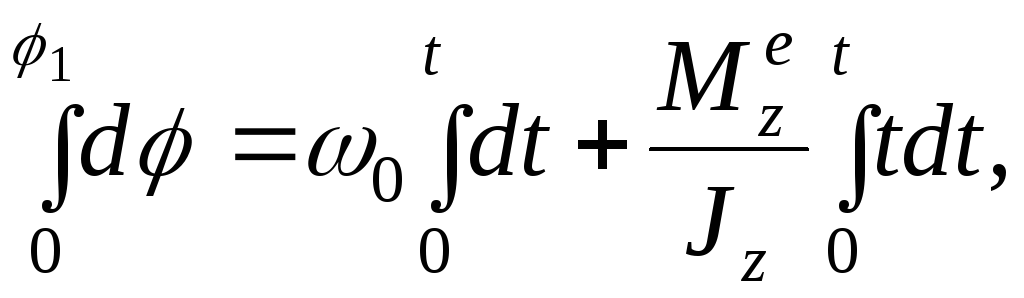
откуда

.

Окончательно имеем рад, что соответствует числу N оборотов шкива: = 19,1 оборотов.

Ответ: t₁ = 12 с; φ₁ = 120 рад.