§ 7. Разыгрывание непрерывной случайной величины.

Метод обратных функций

Пусть требуется разыграть непрерывную случай­ную величину X, т. е. получить последовательность ее возможных значений x_i(i=1,2, ...), зная функцию распределения F(х).

Теорема. Если r_i,—случайное число, то возможное зна­чение x_i разыгрываемой непрерывной случайной величины Х с заданной функцией распределения F(х), соответствующее r_i, является корнем уравнения

F(х_i)=r_i. (»)

Доказательство. Пусть выбрано случайное число r_i (0≤r_i<1). Так как в интервале всех возможных зна­чений Х функция распределения F(х) монотонно возра­стает от 0 до 1, то в этом интервале существует, причем только одно, такое значение аргумента х_i,, при котором функция распределения примет значение r_i. Другими словами, уравнение (*) имеет единственное решение

х_i=F^-1(r_i),

где F^-1—функция, обратная функции у=F(х).

Докажем теперь, что корень х_i уравнения (*) есть возможное значение такой непрерывной случайной вели­чины (временно обозначим ее через ξ, а потом убедимся, что ξ=Х). С этой целью докажем, что вероятность попа­дания ξ в интервал, например (с, d), принадлежащий интервалу всех возможных значений X, равна прираще­нию функции распределения F(х) на этом интервале:

Р(с<ξ<d)=F(d)—F(с).

Действительно, так как F(х)—монотонно возрастаю­щая функция в интервале всех возможных значений X, то в этом интервале большим значениям аргумента соот­ветствуют большие значения функции, и обратно. Поэтому, если с <х_i< d, то F(c)<r_i<F(d), и обратно [учтено, что в силу (*) F(х_i)=r_i].

Из этих неравенств следует, что если случайная величина ξ заключена в интервале

с< ξ < d, ξ (**)

то случайная величина R заключена в интервале

F(с)<R<F(d), (***)

и обратно. Таким образом, неравенства (**) и (***) рав­носильны, а, значит, и равновероятны:

Р(с<ξ<d)=Р[F(с)<R<F(d)]. (****)

Так как величина R распределена равномерно в ин­тервале (0,1), то вероятность попадания R в некоторый интервал, принадлежащий интервалу (0,1), равна его длине (см. гл. XI, § 6, замечание). В частности,

Р[F(с)<R<F(d) ] =F(d) - F(с).

Следовательно, соотношение (****) можно записать в виде

Р(с<ξ<d)= F(d) - F(с).

Итак, вероятность попадания ξ в интервал (с,d) равна приращению функции распределения F(х) на этом интер­вале, а это означает, что ξ=Х. Другими словами, числа х_i, определяемые формулой (*), есть возможные значения величины Х с заданной функцией распределения F(х), что и требовалось доказать.

Правило 1. Для того чтобы найти возможное значение х_i, непрерывной случайной величины X, зная ее функцию распределения F(х), надо выбрать случайное число r_i приравнять его функции распределения и решить отно­сительно х_i, полученное уравнение

F(х_i)= r_i.

Замечание 1. Если решить это уравнение в явном виде не удается, то прибегают к графическим или численным методам.

Пример I. Разыграть 3 возможных значения непрерывной слу­чайной величины X, распределенной равномерно в интервале (2, 10).

Решение. Напишем функцию распределения величины X, рас­пределенной равномерно в интервале (а, b) (см. гл. XI, § 3, пример):

F(х)=(х-а)/(b-а).

По условию, а =2, b =10, следовательно,

F(х)=(х-2)/8.

Используя правило настоящего параграфа, напишем уравнение для отыскания возможных значений х_i, для чего приравняем функцию распределения случайному числу:

(х_i -2)/8=r_i.

Отсюда х_i=8 r_i+2.

Выберем 3 случайных числа, например, r_i=0,11, r_i=0,17, r_i=0,66. Подставим эти числа в уравнение, разрешенное относительно х_i, в итоге получим соответствующие возможные значения X: х₁=8·0,11+2==2,88; х₂=1.36; х₃=7,28.

Пример 2. Непрерывная случайная величина Х распределена по показательному закону, заданному функцией распределения (параметр λ > 0 известен)

F(х)=1 - е^-λх (х>0).

Требуется найти явную формулу для разыгрывания возможных зна­чений X.

Решение. Используя правило настоящего параграфа, напишем уравнение

1 - е^-λхi

Решим это уравнение относительно х_i:

е^-λхi=1 - r_i, или -λх_i=ln(1 - r_i).

Отсюда

х_i=1п(1 – r_i)/λ.

Случайное число r_i заключено в интервале (0,1); следовательно, число 1 - r_i, также случайное и принадлежит интервалу (0,1). Дру­гими словами, величины R и 1 - R распределены одинаково. Поэтому для отыскания х_i можно воспользоваться более простой формулой:

x_i=-ln r_i/λ.

Замечание 2. Известно, что (см. гл. XI, §3)

В частности,

Отсюда следует, что если известна плотность вероятности f(x), то для разыгрывания Х можно вместо уравнений F(x_i)=r_i решить относительно x_i уравнение

Правило 2. Для того чтобы найти возможное значение х_i (непрерывной случайной величины X, зная ее плот­ность вероятности f(x) надо выбрать случайное число r_i и решить относительно х_i, уравнение

или уравнение

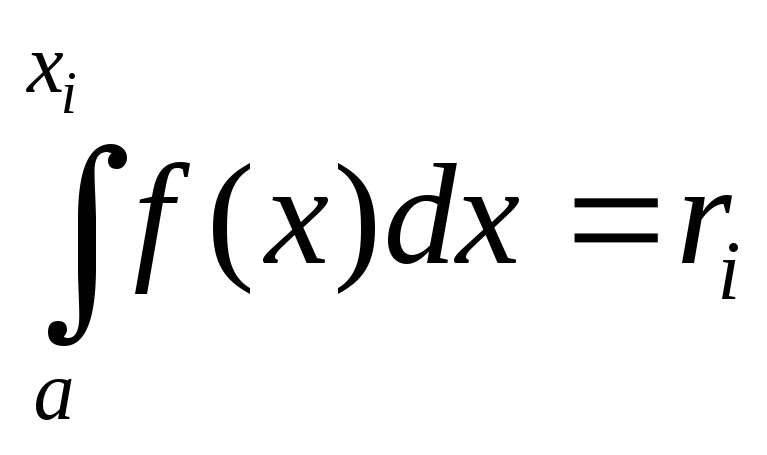
где а—наименьшее конечное возможное значение X.

Пример 3. Задана плотность вероятности непрерывной случайной величины Х f(х)=λ(1—λх/2) в интервале (0; 2/λ); вне этого интер­вала f(х)=0. Требуется найти явную формулу для разыгрывания возможных значений X.

Решение. Напишем в соответствии с правилом 2 уравнение

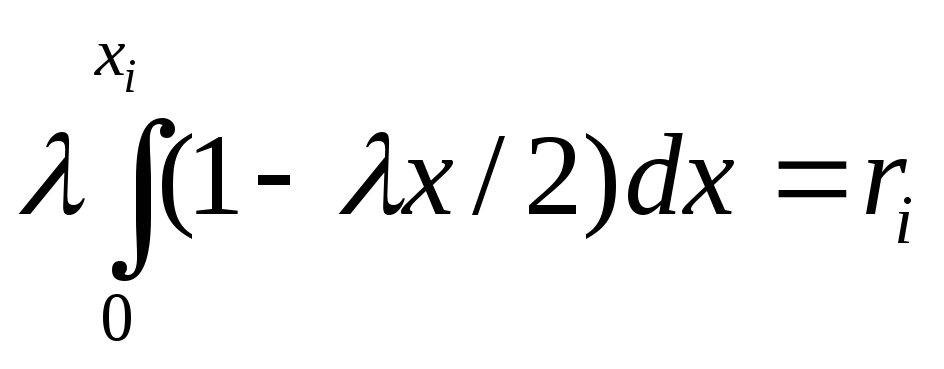
Выполнив интегрирование и решив полученное квадратное уравнение относительно х_i, окончательно получим