2.5. Метод разделения переменных. Струна с закреплёнными концами

Метод разделения переменных, метод Фурье, является одним из наиболее распространенных методов решения уравнений с частными производными.

Посмотрим как работает метод на примере задачи о колебаниях струны, закрепленной на концах:

,

, ,

.

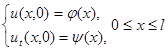Уравнение линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Имея достаточно большое число частных решений, можно попытаться при помощи суммирования их с некоторыми коэффициентами найти искомое решение.

Рассмотрим вспомогательную задачу.

Найти решение уравнения 

не равное тождественно нулю, удовлетворяющее однородным граничным условиям , 

и представимое в виде произведения

.

Подставляя предполагаемое решение  в уравнение, получим равенство

,

Правая и левая часть которого могут быть только константой (не зависят ни от  ни от ):

.

Тогда функции  и  – решения задач

 

(имеется в виду, что функция отлична от тождественного нуля);

 

(имеется в виду, что функция отлична от тождественного нуля).

Для функции получили задачу о собственных значениях (задачу Штурма-Лиувилля).

Найти те значения параметра , при которых существуют нетривиальные решения задачи

а также найти эти решения.

Такие значения параметра называются собственными значениями, а соответствующие им нетривиальные решения — собственными функциями задачи.

Нетривиальные решения задачи Штурма-Лиувилля существуют только при

.

Этим собственным значениям соответствуют собственные функции

.

Для этих значений  имеем

С произвольными постоянными  и .

Тогда функции

являются частными решениями уравнения, удовлетворяющими граничным условиям.

В силу линейности и однородности уравнения сумма частных решений

также удовлетворяет данному уравнению и граничным условиям.

Начальные условия позволяют определить  и :

, .

Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция , заданная в промежутке ,разлагается в ряд Фурье и, следовательно,

, ,

, .

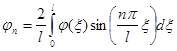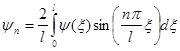Тогда, поскольку

 и 

имеем

, .

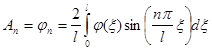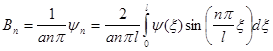Задача решена. Проанализируем полученное решение.

Функцию

можно представить в виде

,

где , .

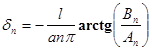Каждая точка струны  совершает гармонические колебания с амплитудой

Движение струны такого типа называется стоячей волной. Точки , , в которых ,

в течение всего процесса остаются неподвижными и называются узлами стоячей волны.

Точки , , в которых , совершают колебания с максимальной амплитудой и называются пучностями стоячей волны.

Профиль стоячей волны в любой момент времени представляет синусоиду

,

, .

В моменты времени, при которых  отклонения максимальны, а скорость равна нулю.

В моменты времени, при которых  отклонения равны нулю, а скорость максимальна.

Колебания струны воспринимаются нами обычно по звуку, издаваемому струной. Можно сказать, что звук струны является наложением «простых тонов»,соответствующих стоячим волнам, на которые разлагается колебание.

Это разложение звука на простые тоны не является операцией только математического характера. Выделение простых тонов можно произвести экспериментально при помощи резонаторов.

Высота тона зависит от частоты колебаний, соответствующих этому тону.

Сила тона определяется его энергией и, следовательно, его амплитудой.

Самый низкий тон, который может издавать струна, определяется самой низкой собственной частотой  и называется основным тоном струны.

Остальные тоны, соответствующие частотам, кратным, называются обертонами. Тембр звука зависит от присутствия наряду с основным тоном обертонов и от распределения энергии по гармоникам.

Низший тон струны и ее тембр зависят от способа возбуждения колебаний.

Действительно, способ возбуждения колебаний определяет начальные условия

 

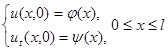
через которые выражаются коэффициентыи .

Если, то низшим тоном будет тон, соответствующий частоте ,где  — наименьшее число, для которого  или отлично от нуля.

Формулы  и ,  определяющие соответственно частоту и период основного колебания, объясняют законы колебания струн, открытые впервые экспериментально (законы Мерсена).

1. Для струн одинаковой плотности и одинакового натяжения период колебания струны пропорционален ее длине.

2. При заданной длине струны период меняется обратно пропорционально корню квадратному из натяжения.

3. При заданной длине и натяжении период меняется пропорционально корню квадратному из линейной плотности струны.

В примере 1 приведен фрагмент рабочего документа Mathcad, содержащего вычисление решения этой смешанной задачи, и продемонстрирована динамика поведения решения.

4.1. Распространение тепла в ограниченном стержне
1. Рассмотрим вначале задачу о распространении тепла в стержне, концы которого поддерживаются при нулевой температуре. Эта задача состоит в отыскании решения уравнения теплопроводности в полуполосе
	(4.1)
при граничных условиях
	(4.2)
и при начальном условии
	(4.3)
где непрерывна, имеет кусочно-непрерывную производную и
Согласно методу Фурье, для частного решения уравнения (4.1) вида получим два уравнения
	(4.4)
	(4.5)
Для удовлетворения граничным условиям (4.2) необходимо потребовать, чтобы
	(4.6)
Изученная ранее спектральная задача (4.5), (4.6) имеет нетривиальные решения вида:
	(4.7)
Значениям параметра соответствуют решения уравнения(4.4)
где произвольные постоянные. Рассмотрим решение исходной задачи(4.1)-(4.3) в виде ряда
	(4.8)
Требуя выполнения начального условия (4.3), получим
	(4.9)
При сделанных выше предложениях на функцию ряд(4.9) с коэффициентами определяемыми по формулам Фурье
	(4.10)
равномерно и абсолютно сходится к Так как при
то ряд (4.8) при также сходится абсолютно и равномерно ви удовлетворяет начальному и граничным условиям. Остаётся показать, что функцияудовлетворяет уравнению(4.1) в области Это следует из того, что ряды, полученные из(4.8) почленным дифференцированием по один раз и подва раза, также абсолютно и равномерно сходятся вв силу того, что при любом
если достаточно велико.

Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает

• электростатическое поле,

• стационарное поле температуры,

• поле давления,

• поле потенциала скорости в гидродинамике.

Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид: 

где — оператор Лапласа или лапласиан, а — вещественная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму:

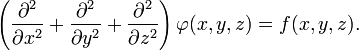
В декартовой системе координат оператор Лапласа записывается в форме и уравнение Пуассона принимает вид:

Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):

Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».

Содержание   [убрать]  1 Электростатика 2 Потенциал точечного заряда 3 Потенциал гауссовой объёмной плотности заряда 4 См. также 5 Ссылки