
- •1. Классификация уравнений второго порядка
- •Лекция 4. Вывод уравнения теплопроводности
- •Начальные условия и граничные условия.
- •Решение первой начально-краевой задачи для уравнения теплопроводности.
- •Лекция 2. Вывод уравнения колебания струны
- •Начальные условия и граничные условия.
- •I. Граничные условия первого рода
- •II. Граничные условия второго рода
- •III. Граничные условия третьего рода
- •Уравнение Лапласа
- •2.5. Метод разделения переменных. Струна с закреплёнными концами
- •[Править]Электростатика
- •[Править]Потенциал точечного заряда
- •[Править]Потенциал гауссовой объёмной плотности заряда
I. Граничные условия первого рода
U|x=0 = g1(t), U|x=l = g2(t)
(5)
Эти условия физически означают, что на концах заданы режимы колебаний.
II. Граничные условия второго рода
Ux|x=0 = g1(t), Ux|x=l = g2(t)
(6)
Такие условия соответствуют тому, что на концах заданы силы.
III. Граничные условия третьего рода
(Ux-σ1U)|x=0 = g1(t) , (Ux –σ2U)|x=l = g2(t)
(7)
Эти условия соответствуют упругому закреплению концов.
Граничные условия (5), (6) и (7) называются однородными, если правые части g1(t) и g2(t) тождественно равны нулю при всех значениях t. Если хотя бы одна из функций в правых частях не равна нулю, то граничные условия называются неоднородными.
Аналогично формулируются граничные условия и в случае трех или четырех переменных при условии, что одна из этих переменных - время. Границей в этих случаях будет или замкнутая кривая Г, ограничивающая некоторую плоскую область, или замкнутая поверхность Ω, ограничивающая область в пространстве. Соответственно изменится и производная от функции, фигурирующая в граничных условиях второго и третьего рода. Это будет производная по нормали n к кривой Г на плоскости или к поверхности Ω в пространстве, причем, как правило, рассматривают нормаль, внешнюю по отношению к области(см.рис.5).
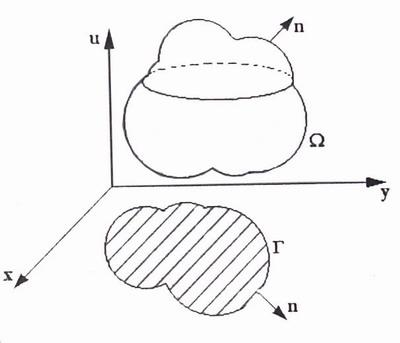
Рис. 5
К
примеру, граничное условие (однородное)
первого рода на плоскости записывается
в виде U|Γ=О,
в пространствеU|Ω=0.
Граничное условие второго рода на
плоскости имеет вид 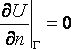 ,а
в пространстве
,а
в пространстве 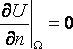 .
Конечно, физический смысл этих условий
разный для различных задач.
.
Конечно, физический смысл этих условий
разный для различных задач.
При постановке начальных и граничных условий возникает задача об отыскании решения дифференциального уравнения, удолетворяющего заданным начальным и граничным (краевым) условиям. Для волнового уравнения (3) или (4), начальных условий U(x,0)=φ(x), Ut(x,0)=ψ(x) и в случае граничных условий первого рода (5), задача называетсяпервой начально-краевой задачей для волнового уравнения. Если вместо граничных условий первого рода задавать условия второго рода (6) или третьего рода (7), то задача будет называться, соответственно, второй и третьей начально-краевой задачей. Если граничные условия на разных участках границы имеют различные типы, то такие начально-краевые задачи называют смешанными.
Рассмотрим две типичных электростатических задачи [1]:
1) Найти потенциал электрического поля при неизвестном местоположении исходных зарядов, но заданном электрическом потенциале на границах области. (Например, задача о распределении потенциала электрического поля, создаваемого системой неподвижных проводников, помещенных в вакуум и подключенных к батареям. Здесь можно измерить потенциал каждого проводника, но задать распределение электрических зарядов на проводниках, зависящее от их формы, весьма сложно.)
2)
Найти потенциал электрического поля,
создаваемого заданным распределением
в пространстве электрических зарядов ![]() .
.
Хорошо
известно, что прямой метод вычисления
потенциала электрического поля ![]() в
этих задачах состоит в решении уравнения
Лапласа (задача
1)
в
этих задачах состоит в решении уравнения
Лапласа (задача
1)
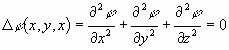 (1)
(1)
и уравнения Пуассона (задача 2)
![]() .
(2)
.
(2)
Уравнения (1), (2) относится к классу дифференциальных уравнений в частных производных эллиптического типа.
Далее мы будем рассматривать только частный случай эллиптических уравнений для поля , зависящего от двух пространственных переменных. Совершенно очевидно, что для полного решения задачи уравнения (1), (2) необходимо дополнить граничными условиями. Различают три типа граничных условий:
1) граничные условия Дирихле (значения задаются на некоторой замкнутой кривой в плоскости (х,у) и, возможно, на некоторых дополнительных кривых, расположенных внутри области (рис. 1));
2) граничные условия Неймана (на границе задается нормальная производная потенциала );
3) смешанная краевая задача (на границе задается линейная комбинация потенциала и его нормальной производной).
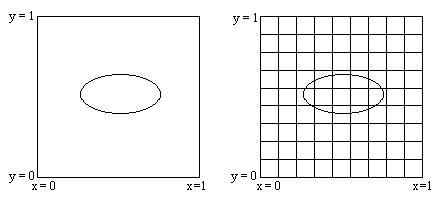
Рис.1
