
- •1. Классификация уравнений второго порядка
- •Лекция 4. Вывод уравнения теплопроводности
- •Начальные условия и граничные условия.
- •Решение первой начально-краевой задачи для уравнения теплопроводности.
- •Лекция 2. Вывод уравнения колебания струны
- •Начальные условия и граничные условия.
- •I. Граничные условия первого рода
- •II. Граничные условия второго рода
- •III. Граничные условия третьего рода
- •Уравнение Лапласа
- •2.5. Метод разделения переменных. Струна с закреплёнными концами
- •[Править]Электростатика
- •[Править]Потенциал точечного заряда
- •[Править]Потенциал гауссовой объёмной плотности заряда
Уравнение Лапласа
[править]
Материал из Википедии — свободной энциклопедии
Уравнение Лапласа — дифференциальное уравнение в частных производных. В трёхмерном пространстве уравнение Лапласа записывается так:
![]()
и является частным случаем уравнения Гельмгольца.
Уравнение рассматривают также в двумерном и одномерном пространстве. В двумерном пространстве уравнение Лапласа записывается:
![]()
Также и в n-мерном пространстве. В этом случае нулю приравнивается сумма n вторых производных.
С помощью дифференциального оператора
![]()
— (оператора
Лапласа) —
это уравнение записывается (для любой
размерности) одинаково как ![]()
В этом случае размерность пространства указывается явно (или подразумевается).
Уравнение Лапласа относится к эллиптическому виду. Функции, являющиеся решениями уравнения Лапласа, называются гармоническими функциями. Неоднородное уравнениеЛапласа называется уравнением Пуассона.
Замечание: всё сказанное выше относится к декартовым координатам в плоском пространстве (какова бы ни была его размерность). При использовании других координат представление оператора Лапласа меняется, и, соответственно, меняется запись уравнения Лапласа (пример — см. ниже). Эти уравнения также называются уравнением Лапласа, однако для устранения неоднозначности терминологии при этом обычно явно добавляется указание системы координат (и, при желании полной ясности, размерности), например: "двумерное уравнение Лапласа в полярных координатах".
. Уравнение колебаний струны
1.1. Уравнение малых поперечных колебаний
Уравнение
колебаний струны относится к уравнениям
гиперболического типа.
Каждую
точку струны можно охарактеризовать
значением ее абсциссы x.
Для определения положения струны в
момент времени t достаточно
знать компоненты вектора смещения
точки x![]() в
момент времени t.
Будем
предполагать, что смещения струны лежат
в одной плоскости (x,U)
и что вектор смещения
в
момент времени t.
Будем
предполагать, что смещения струны лежат
в одной плоскости (x,U)
и что вектор смещения
![]() перпендикулярен
в любой момент времени к оси x;
тогда процесс колебания можно описать
одной функцией U(x,t)
(смотри рисунок) .
перпендикулярен
в любой момент времени к оси x;
тогда процесс колебания можно описать
одной функцией U(x,t)
(смотри рисунок) .
Функция U(x,t) характеризует вертикальное перемещение струны.
|
а=const- зависит от упругости, жесткости, массы и т. д.
Существуют следующие методы решения уравнения колебаний струны:
|
|
1.2. Метод Даламбера (метод бегущих волн, метод характеристик)
Рассмотрим неограниченную струну и зададим начальные условия:
Уравнение решается в явном виде с помощью замены переменных:
Интегрируя это равенство по η при фиксированном ξ, получим:
Вернемся к старой переменной:
Функция (3) является общим интегралом уравнения (1). Теперь необходимо удовлетворить начальным условиям (2):
Интегрируя (5), получим:
Из равенств (4) и (6) находим
Выражения (7), (8) подставляем в (3).
| ||||||||||||||||||||||
|
|


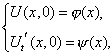
 ,
где
,
где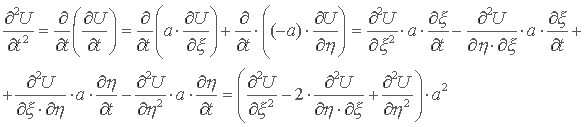
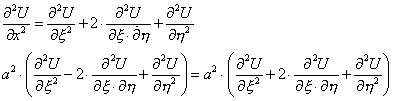
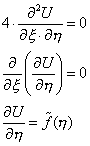
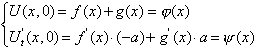 .
.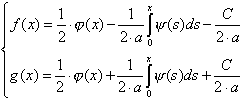 .
. .
.