
Учебное пособие по начертательной геометрии
.pdf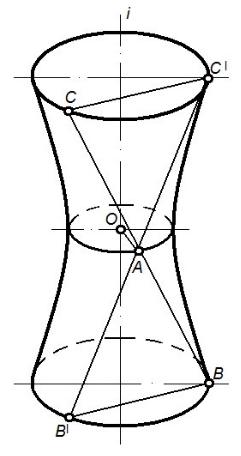
Рисунок 51 – Поверхность вращения – однополостный гиперболоид
7.4 Поверхности, образуемые при вращении окружности
Сфера
Тело, полученное от вращения полукруга вокруг диаметра, называется шаром, а поверхность, образуемая при этом окружностью, называется сферической (рисунок 52).
Можно также сказать, что эта поверхность есть геометрическое место точек, одинаково удаленных от одной и той же точки, называемой центром. Отрезок, соединяющий центр с какой-нибудь точкой поверхности, называется радиусом, а отрезок, соединяющий две точки поверхности и проходящий через центр, называется диаметром сферы.
61
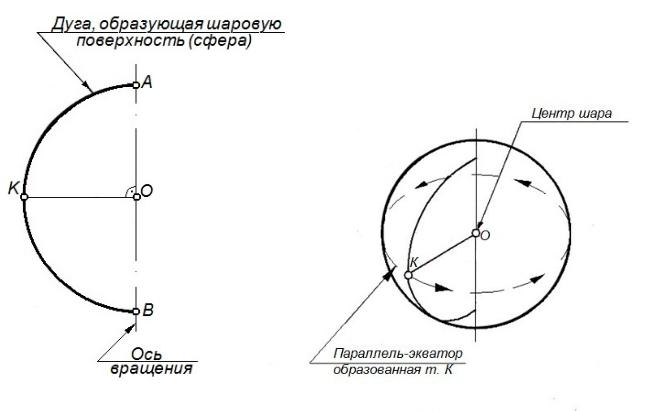
На рисунке 52 ось вращения сферической поверхности совпадает с вертикальным диаметром.
Всякая проекция сферической поверхности является окружностью, очерками проекций на плоскость П1 является проекция экватора, на плоскость П2 и П3 являются проекции меридианов.
Рисунок 52 – Поверхность вращения - сфера
На рисунке 53 отмечены проекции оси i, экватора b, фронтального меридиана а и профильного l.
Задача 1. Построить проекции точек А и В, принадлежащие сфере рисунок 53.
Недостающие проекции точек, определяются с помощью параллелей, которым эти точки принадлежат.
Видимость точек А и В определена в зависимости от того, на какой части сферы они лежат (на видимой части – видимы, на невидимой – невидимы).
62
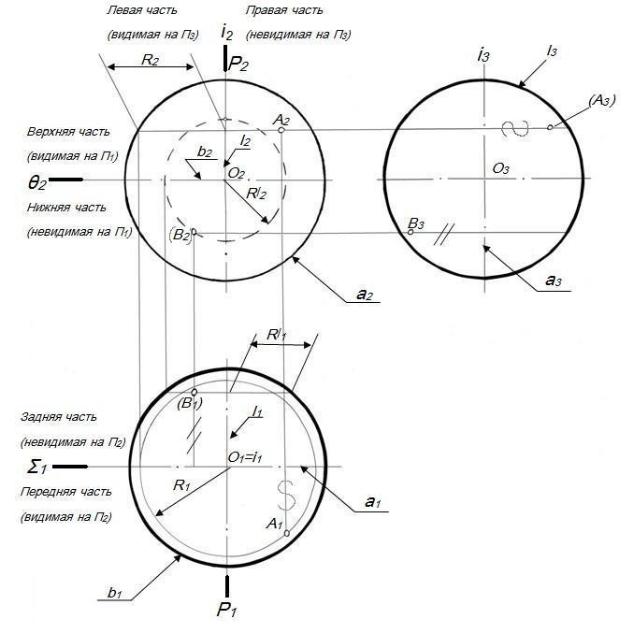
Рисунок 53 – Определение видимости сферы
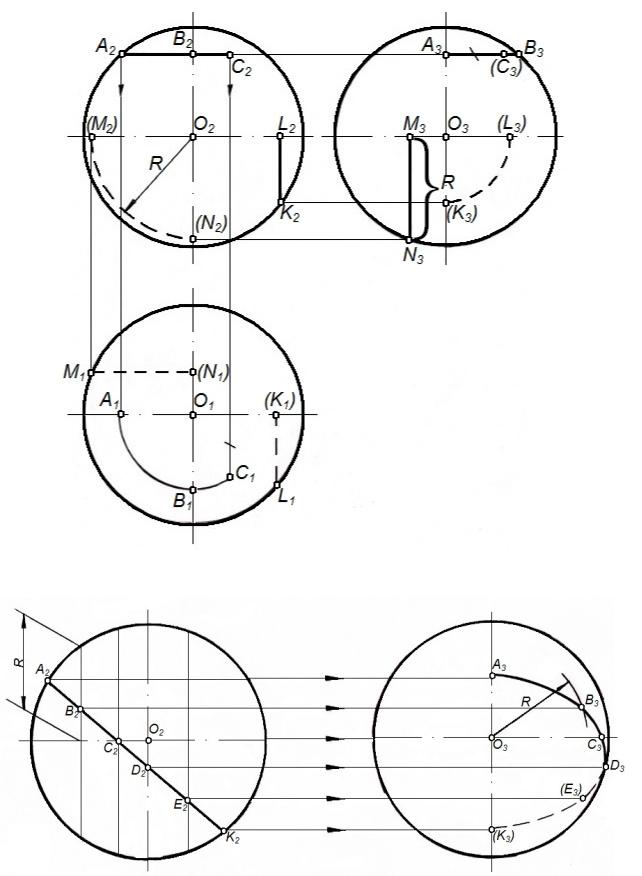
Задача 2. Построить недостающие проекции видимых линий, принадлежащих поверхности сферы.
На рисунке 54а показано построение А1В1С1 и А3В3С3 по заданной А2В2С2; L1K1 и L3K3 по заданной L2K2; M2N2 и M1N1 по заданной M3K3.
На рисунке 54б показано построение А3В3С3D3E3K3 по заданной
А2В2С2D2E2K2.
63
а)
б)
Рисунок 54 – Построение линий на поверхности сферы
64
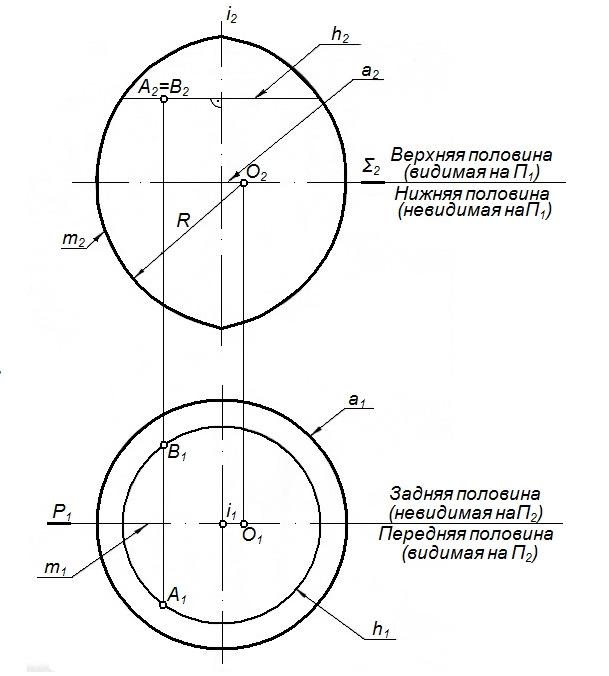
Закрытый тор
Закрытый тор образован вращением дуги окружности радиуса R вокруг оси i, расположенной в плоскости окружности, но не проходящий через ее центр, причем ось вращения имеет с окружностью две общие точки (рисунок
55).
Рисунок 55 – Поверхность вращения - закрытый тор
65
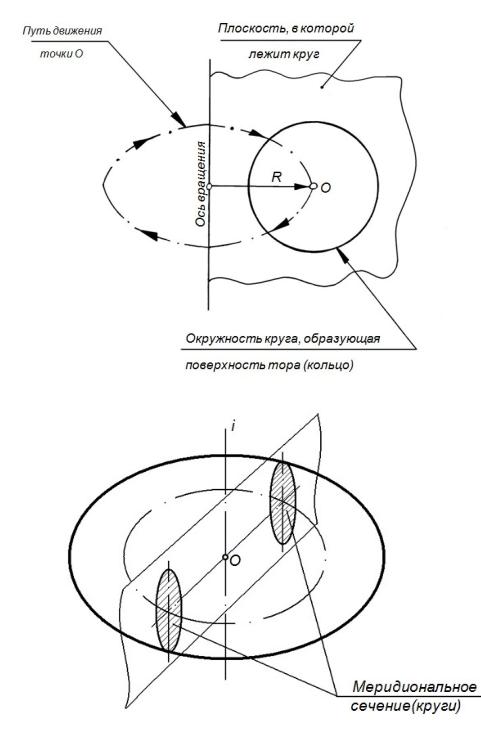
Открытый тор (круговое кольцо)
Открытым тором называется тело, полученное от вращения окружности (образующей) вокруг оси, расположенной в её плоскости, но не проходящей через ее центр, причем ось вращения не имеет общих точек с окружностью (рисунок 56).
Рисунок 56 – Поверхность вращения – открытый тор
66
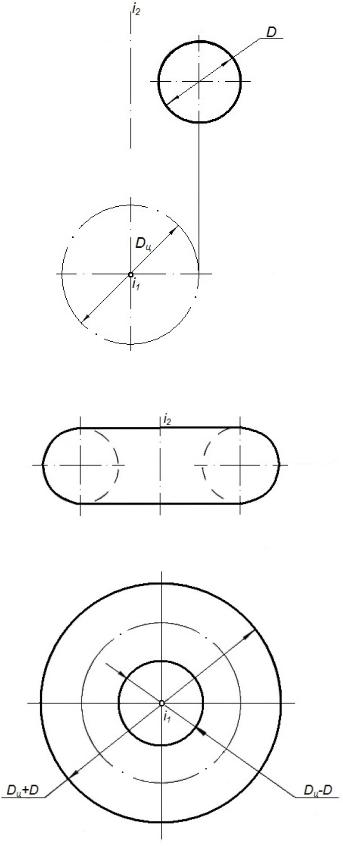
а)
б)
Рисунок 57 - Комплексный чертеж тора
67
i – ось кольца ( П1) D – диаметр окружности центров образующих окружностей (рисунок 57а). Горизонтальная проекция кольца (рисунок 57б) выразится двумя концентрическими окружностями Dц+D и Dс-d. Фронтальная проекция кольца выразится двумя образующими окружностями, сопряженными прямыми.
Принадлежность линии и точки поверхности тора
Задача 1 Задать точку на поверхности тора.
Рисунок 58 – Точки на поверхности тора
Построение проекций точек, принадлежащих тору, выполняется с помощью окружностей, которым точки принадлежат. На поверхности тора можно выделить два семейства окружностей. Например, точка А принадлежит
68
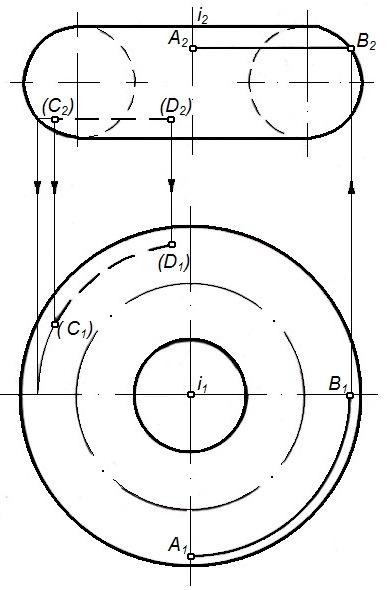
окружности m, радиус которой измеряется от оси тора до очерка наружной поверхности, а точка В принадлежит окружности n, радиус которой измеряется от оси до очерка внутренней поверхности тора (рисунок 58).
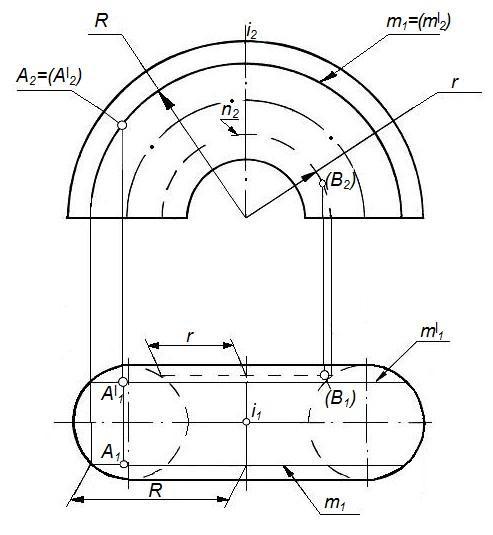
Задача 2 Построить недостающие проекции линий, принадлежащих поверхности тора.
Рисунок 59 – Построение недостающих проекций на поверхности тора
На рисунке 59 показано построение недостающих проекций А2В2 и С1D1, если заданы A1B1 и C2D2.
69
8 Позиционные задачи понятия и определения
Круг задач, ответы на которые могут быть получены графическим путем, чрезвычайно широк. При этом независимо от степени сложности их решения, все они могут быть отнесены к одному из двух классов: метрические или позиционные. Это деление является условным, но, несмотря на это, распределение задач по классам в методическом отношении имеет большой смысл, так как позволяет установить единые алгоритмы решения задач, входящих в один класс.
Под позиционными задачами подразумеваются задачи, решение которых позволяет получить ответ о принадлежности элемента (точки) или подмножества (линии) множеству (поверхности).
Первая группа позиционных задач может быть объединена под общим названием – задачи на принадлежность (эта группа задач рассмотрена ранее).
Ко второй группе относятся задачи на пересечение. Эта группа содержит три типа задач:
1.пересечение линии с линией;
2.пересечение поверхности с поверхностью;
3.пересечение линии с поверхностью.
С точки зрения единства принципа, положенного в основу решения позиционных задач, их можно не делить на две группы. Подходя к позиционным задачам с таких позиций, можно считать, что все многообразие позиционных задач может быть сведено к решению задач первой группы – задач на принадлежность. Вот почему ранее в данном пособии было обращено большое внимание на решение задач первой группы:
1.принадлежность точки линии;
2.принадлежность точки поверхности;
3.принадлежность линии поверхности.
70
