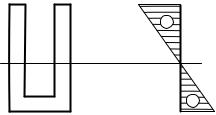
87 ÌÏà

Ýσ

–

+

70 ÌÏà

Рисунок 2.11

2.6. Расчет на жесткость при изгибе балки

При решении задач на жесткость при прямом изгибе перемещения в заданной точке оси балки (прогиб f или угол поворота сечения θ) определяют с помощью интеграла Мора

где n — число силовых участков балки; MP — аналитическое выражение изгибающего момента как функции от координаты z при действии внешних сил (включая реакции опор); M1P то же при действии только единичной силы, приложенной в заданной точке; M1M — при действии только единичного момента; EIx — жесткость сечения балки в плоскости изгиба.

При определении перемещений рассматривают два состояния системы: первое — «основное» с приложенными действующими нагрузками, второе — «единичное», когда действует лишь одна безразмерная сосредоточенная сила P = 1 (при определении линейного перемещения f ) или один безразмерный сосредоточенный момент M = 1 (при определении угла поворота θ). Единичную силу или единичный момент прикладывают в точке балки, где определяют соответствующее перемещение, по направлению искомого перемещения. Строят эпюры изгибающего момента для каждого состояния — грузовую ЭMP и единич- ную ЭM1.

68

При вычислении интеграла для упрощения расчетов используют графоаналитические способы.

Способ Верещагина. Перемещение в точке определяют по формуле

δ = ΩMc ,

EIx

где Ω — площадь грузовой эпюры изгибающего момента; Mc — ордината единичной эпюры под центром тяжести площади грузовой эпюры (рисунок 2.12, а).

Эпюры должны удовлетворять следующим условиям:

1)грузовая эпюра ЭMP непрерывна и сохраняет знак на всем участке интегрирования;

2)площадь и положение центра тяжести грузовой эпюры известны или легко определяются;

3)единичная эпюра является линейной;

4)жесткость сечения EIx постоянная.

Эпюры разбивают на n простых фигур (участков), удовлетворяющих перечисленным условиям, и перемещение вычисляют по формуле

69

Формула Мюллера-Бреслау. Перемещение в точке определяют по формуле

ãäå li — длина i-го участка эпюры; величины Аi, Âi, ai, bi, fi показаны на рисунке 2.12, б.

Формула Симпсона. Перемещение в точке определяют по формуле

ãäå Ài, Âi, Ñi, ai, bi, ci показаны на рисунке 2.12, в.

Пример 10

Для балки прямоугольного сечения, показанной на рисунке 2.13, изготовленной из пластичного материала, требуется:

1)построить эпюры внутренних силовых факторов;

2)из условия прочности определить допускаемое значение параметра нагрузки Pmax,

3)определить прогиб балки в точке А и угол поворота се- чения в точке В.

70

Исходные данные: размеры сечения балки — ширина b, высота h; параметр длины балки l = 0,1 м; коэффициент запаса nò = 2,0. Остальные данные приведены в таблице 2.12.

Решение

1.Изображаем реальную схему задачи (рисунок 2.14, а).

2.Записав уравнения равновесия балки, определяем реакции опор RyB è RyC:

Используя метод сечений, строим эпюры поперечной силы ЭQ и изгибающего момента ЭМ (рисунок 2.14, б).

3. Расчет грузоподъемности балки выполняем с использованием условия прочности при изгибе

Для сечения прямоугольной формы момент сопротивления Wx определяем по формуле

Следовательно, значение параметра нагрузки

71

A

0,5l

ÝM1

â

M = 1

B

1

ÝM1

ã

Рисунок 2.14

72

Итак, допускаемое значение параметра нагрузки

Pmax = 2,13 10−3 МН или 2,13 кН .

4. Для определения прогиба в точке А по методу Мора необходимо приложить в рассматриваемой точке единичную силу, построить эпюру моментов от действия этой силы (единичную эпюру ЭМ1) и умножить ее на полученную ранее грузовую эпюру ЭМP. Для построения эпюры моментов ЭМ1 с расчетной схемы балки убираем все внешние силы и моменты, в точке А прикладываем силу, равную 1 (рисунок 2.14, в).

Записав уравнения равновесия, определяем реакции опор:

RyВ = 0,5; RyC = 0,5 . Эпюра ЭМ1 показана на рисунке 2.14, в.

При перемножении эпюр используем графоаналитические способы: способ Верещагина, формулу Мюллера-Бреслау и формулу Симпсона. Для иллюстрации их применения вычислим прогиб в точке А каждым из способов.

Способ Верещагина:

Формула Мюллера-Бреслау:

73

С учетом того, что момент инерции сечения

величина прогиба в точке А

Таким образом, прогиб в точке А

fА = 34,1 10−6 м = 3,41 10−2 мм .

Знак «+» означает, что направление перемещения сечения балки совпадает с направлением действия приложенной единичной силы.

5. Для определения угла поворота сечения в точке В по методу Мора необходимо приложить в рассматриваемой точке единичный момент, построить единичную эпюру ЭМ1 и умножить ее на полученную ранее грузовую эпюру ЭМP.

Для построения эпюры моментов ЭМ1 удаляем с расчетной схемы балки все внешние силы и моменты, в точке В прикладываем момент M = 1 (рисунок 2.14, г).

Записав уравнения равновесия, определяем реакции опор:

RyB = − 1 , RyC = 1 .

2l 2l

Эпюра ЭМ1 показана на рисунке 2.14, г.

Угол поворота сечения В определим перемножением эпюр с использованием формулы Симпсона:

Окончательно величина угла поворота сечения В с учетом полученного выше значения момента инерции

74

Таким образом, угол поворота сечения В

θВ = −1,4 10−3 рад = −0,16° .

Знак «–» означает, что поворот сечения направлен противоположно приложенному единичному моменту.

75

ЧАСТЬ 3

РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ

Статически неопределимыми называют стержневые системы, у которых число связей превышает число уравнений равновесия для этой системы. Поэтому для определения реакций опор необходимо составлять дополнительные уравнения — уравнения перемещений.

Степень статической неопределимости равна числу «лишних» связей, удаление которых превращает стержневую систему в статически определимую геометрически неизменяемую систему. Полученная в результате этого система называется основной системой. В основной системе перемещения по направлениям отброшенных связей должны быть равны нулю. Следовательно, реакции отброшенных связей должны иметь такие значения, при которых перемещения по их направлениям равнялись бы нулю. Для определения этих реакций записывают систему канонических уравнений метода сил, которая представляет собой условие эквивалентности заданной и основной систем:

ãäå X1...Xn — неизвестные реакции отброшенных связей; δ11... δnn — единичные перемещения; 1P... nP — перемещения в основной системе.

Число канонических уравнений равно числу отброшенных связей, т.е. степени статической неопределимости заданной системы.

Первый из каждого двойного индекса показывает номер отброшенной связи и соответствующее направление перемещения, второй дает причину перемещения. iP есть перемещение

76

в основной системе в направлении i-й отброшенной связи (т.е. перемещение в точке, где находилась i-я «лишняя» связь, под влиянием внешних сил, действующих в основной системе). Коэффициент δik представляет собой перемещение по направлению i-й отброшенной связи, вызванное единичной силой, действующей в направлении k-й отброшенной связи.

Для определения перемещений необходимо построить грузовую эпюру момента ЭMP для основной системы, нагруженной внешними силами, и эпюры моментов для основной системы при действии åдиничных сил, приложенных в местах удаленных связей ЭMi .

Перемещение kP вычисëяют путем умножения эпюры ЭMP на единичную эпюру ЭMk , а перемещение δik — путем перемножения единичных эпюр ЭMi è ЭMk :

kP = ЭMP × ЭMk , δik = ЭMi × ЭMk .

Затем систему канонических уравнений решают относительно неизвестных Xi и строят окончательную эпюру моментов для заданной стержневой системы. В дальнейшем выполняют расчет конструкции на прочность.

Пример 11

Для плоской статически неопределимой рамы (рисунок 3.1) необходимо:

1)построить эпюры внутренних силовых факторов;

2)из расчета на прочность определить размеры коробча- того сечения.

Исходные данные: параметр нагрузки P = 60 кН, допускаемые напряжения [σ] = 160 МПа. Остальные данные приведены

âтаблице 3.1.

Решение

1.Изображаем реальную схему задачи (рисунок 3.2, а).

2.Определяем степень статической неопределимости стержневой системы.

77

На раму наложены пять связей (рисунок 3.2, а), обозначенные реакциями RyA, RyB, RzB, RyC, RzC. Для плоской системы мы можем записать три уравнения равновесия. Таким образом, степень статической неопределимости рамы S = 5 – 3 = 2, система дважды статически неопределима.

Для превращения рамы в статически определимую основную систему отбрасываем две «лишние» связи — в точке А в направлении оси y и в точке С в направлении оси x (рисунок 3.2, б).

Система канонических уравнений метода сил имеет вид

δ11X1 + δ12 X2 + 1P = 0

δ + δ + =

21X1 22 X2 2P 0.

Здесь 1P, 2P — перемещения в основной системе в точ- ках расположения удаленных связей в направлении этих удаленных связей от действия внешних сил (т.е. в точке А в направлении оси y и в точке С в направлении оси z);

78

δ11 — перемещение в основной системе (с удаленными «лишними» связями) в точке первой удаленной связи по направлению этой связи от действия единичной силы, приложенной в этой точке и направленной вдоль первой удаленной связи (т.е. в точке А в направлении оси y от единичной силы, приложенной в этой точке и направленной вдоль оси y);

δ12 — перемещение в точке А от действия единичной силы, приложенной в точке второй удаленной связи по направлению этой связи (т.е. в точке А в направлении оси у от единичной силы, приложенной в точке C и направленной вдоль оси z);

δ21 — соответственно перемещение в точке С в направлении оси z от единичной силы, приложенной в точке А и направленной вдоль оси y;

δ22 — перемещение в точке С в направлении оси z от единичной силы, приложенной в этой же точке и направленной вдоль оси z.

3. Для основной системы определяем реакции опор RyB, RzB, RyC с использованием уравнений равновесия

ΣPz = RzB − P = 0,

ΣPy = RyB + RyC − 3P = 0,

ΣMB = P 2l − 3P l + RyC 2l = 0,

RyB = 5P/ 2 , RzB = P, RyC = P/ 2 .

Эпюра зигибающего момента для основной системы ЭMP показана на рисунке 3.2, б.

4. Получаем эпюру изгибающего момента ЭM1 от единич- ной силы, приложенной в направлении первой удаленной связи. Для этого, удалив все внешние силы, в точке А основной системы прикладываем силу P = 1 (рисунок 3.2, в) и определяем реакции опор:

ΣZi = RzB = 0,

ΣYi = RyB + RyC −1 = 0,

ΣMB = 1 2l + RyB 2l = 0,

RyB = 1,5, RzB = 0, RyC = −0,5.

79

á

1 1·l

ЭM1

â

Рисунок 3.2 (а, б, в)

80

ã

ä

Рисунок 3.2 (г, д)

81

Эпюра ЭM1 показана на рисунке 3.2, в. Аналогичным образом строим эпюру изгибающего момента ЭM2 от действия единичной силы, приложенной в направлении второй удаленной связи (рисунок 3.2, г).

5. Используя формулу Симпсона, рассчитываем перемеще-

82

Подставив вычисленные значения перемещений в систему канонических уравнений, после упрощений получаем

Решаем систему уравнений относительно неизвестных X1 è X2:

В результате получаем статически определимую стержневую систему (рисунок 3.2, д). Для этой системы окончательно определяем реакции опор и строим эпюры внутренних силовых факторов — продольной силы ЭN, поперечной силы ЭQ и изгибающего момента ЭМ (рисунок 3.2, д).

Проверка правильности построения итоговой эпюры изгибающего момента ЭM выполняется ïóòåì ïåðåмножения ее на любую из «единичных» эпюр — ЭM1 èëè ЭM2 . Это произведение должно быть равно нулю.

6. Анализ силовой схемы показывает, что стержни рамы находятся в условиях комбинированного нагружения — соче- тания поперечного изгиба и растяжения (сжатия). Напряженное состояние при этом одноосное, т.к. и при изгибе, и при растяжении (сжатии) в точках поперечного сечения возникают напряжения, действующие вдоль продольной оси стержня — нормальные напряжения. Поэтому в точке сечения полное нормальное напряжение вычисляем как сумму двух составляющих — от действия продольной силы и от действия изгибающего момента:

σ = N + M ymax .

F Ix

7. Для заданного сечения (см. рисунок 3.1) определяем необходимые геометрические характеристики: площадь сечения F, момент инерции Ix и координату опасной точки ymax:

83

F = 15a 30a −13a 28a = 86a2 ,

ymax = 15a.

Для расчета толщины стенки сечения a записываем условие прочности для каждого из стержней рамы:

Приведенные уравнения позволяют получить значение толщины стенки для каждого из стержней:

a1 ≥ 6,3 (мм), a2 ≥ 5,5 (мм), a3 ≥ 7,7 (мм) .

Исходя из полученных данных, опасным является третий стержень, поэтому для всей конструкции принимаем величину толщины стенки сечения a = 8 мм. Соответственно, ширина коробчатого профиля должна быть 120 мм, высота — 240 мм.

84