
Министерство образования и науки РФ
Новосибирский государственный университет экономики и управления
Кафедра прикладных информационных технологий
КУРСОВАЯ РАБОТА
по дисциплине «Информационные технологии»
на тему:
Разработка программного обеспечения для проверки качества одномерной линейной регрессионной модели.
Выполнил: студент группы 8095
ФИО: Русановский Константин Сергеевич
№ зачетной книжки 081625
Проверил: Осипов Александр Леонидович
Оценка ____________________________
Дата ______________________________
Новосибирск 2012
Оглавление
Введение 2
Цели и задачи курсовой работы 4
Регрессионный анализ 5
Нахождение уравнения регрессии 12
Проверка адекватности модели регрессии 14
Построение точечного прогноза 20
Интерейс 21
Список литературы 22
Введение
Математическая постановка задачи регрессии заключается в следующем. Зависимость величины (числового значения) определенного свойства случайного процесса или физического явления Y от другого переменного свойства или параметра Х, которое в общем случае также может относиться к случайной величине, зарегистрирована на множестве точек xk множеством значений yk, при этом в каждой точке зарегистрированные значения yk и xk отображают действительные значения Y(хk) со случайной погрешностью k, распределенной, как правило, по нормальному закону. По совокупности значений yk требуется подобрать такую функцию f(xk, a0, a1, …, an), которой зависимость Y(x) отображалась бы с минимальной погрешностью.
Цели и задачи курсовой работы
Цель работы – овладеть методикой построения линейных моделей парной регрессии, оценки их существенности и значимости, расчетом показателей парной регрессии и корреляции.
Постановка
задачи. По данным изучаемых регионов
(таблица 1) изучить зависимость общего
коэффициента рождаемости (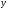 )
от уровня бедности, % (
)
от уровня бедности, % (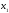 )
и среднедушевого дохода, тыс. руб. (
)
и среднедушевого дохода, тыс. руб. ( ).
).
Таблица 1. Исходные данные для корреляционно-регрессионного анализа
|
Регион |
x1 |
x2 |
y |
|
1Орловская область |
7,2 |
19,9 |
9,6 |
|
2 Рязанская область |
8,1 |
17,1 |
9,4 |
|
3 Смоленская область |
8,4 |
17,4 |
9,6 |
|
4 Тамбовская область |
8,6 |
13,5 |
8,9 |
|
5 Тверская область |
8,6 |
14,8 |
10,2 |
|
6 Тульская область |
8,4 |
14,2 |
8,4 |
|
7 Ярославская область |
9,9 |
15,1 |
9,9 |
|
8 Республика Карелия |
10,1 |
17 |
10,6 |
|
9 Республика Коми |
16,2 |
14,5 |
11,9 |
|
10 Архангельская область |
11,6 |
16,1 |
11,9 |
|
11 Вологодская область |
10,5 |
14,8 |
11,6 |
|
12 Калининградская область |
11,4 |
12,4 |
10,9 |
|
13 Ленинградская область |
10,6 |
12,6 |
8,3 |
|
14 Мурманская область |
15,2 |
15,5 |
10,3 |
|
15 Новгородская область |
8,6 |
20,3 |
10,7 |
|
16 Псковская область |
7,9 |
17,1 |
9,7 |
|
17 Республика Адыгея |
5,8 |
30,4 |
11,8 |
|
18 Республика Дагестан |
8 |
13,8 |
17 |
|
19 Респ-ка Ингушетия |
4 |
44,8 |
16,7 |
|
20 Кабардино-Балкарская Республика |
6,6 |
18,3 |
12,8 |
|
21 Респ-ка Калмыкия |
4,5 |
44,2 |
14,5 |
|
22 Карачаево-Черкесская Республика |
6,9 |
18,3 |
14,2 |
|
23 Республика Северная Осетия - Алания |
7,9 |
12,9 |
13,6 |
|
24 Чеченская Республикака |
… |
... |
27,1 |
|
25 Краснодарский край |
9,8 |
19,2 |
11,3 |
Регрессионный анализ
Одной из типовых задач обработки многомерных ЭД является определение количественной зависимости показателей качества объекта от значений его параметров и характеристик внешней среды. Примером такой постановки задачи является установление зависимости между временем обработки запросов к базе данных и интенсивностью входного потока. Время обработки зависит от многих факторов, в том числе от размещения искомой информации на внешних носителях, сложности запроса. Следовательно, время обработки конкретного запроса можно считать случайной величиной. Но вместе с тем, при увеличении интенсивности потока запросов следует ожидать возрастания его среднего значения, т.е. считать, что время обработки и интенсивность потока запросов связаны корреляционной зависимостью.
Постановка задачи регрессионного анализа формулируется следующим образом.
Имеется совокупность результатов наблюдений. В этой совокупности один столбец соответствует показателю, для которого необходимо установить функциональную зависимость с параметрами объекта и среды, представленными остальными столбцами. Будем обозначать показатель через y* и считать, что ему соответствует первый столбец матрицы наблюдений. Остальные т–1 (m > 1) столбцов соответствуют параметрам (факторам) х2, х3, …, хт .
Требуется: установить количественную взаимосвязь между показателем и факторами. В таком случае задача регрессионного анализа понимается как задача выявления такой функциональной зависимости y* = f(x2 , x3 , …, xт), которая наилучшим образом описывает имеющиеся экспериментальные данные.
Допущения:
количество наблюдений достаточно для проявления статистических закономерностей относительно факторов и их взаимосвязей;
обрабатываемые ЭД содержат некоторые ошибки (помехи), обусловленные погрешностями измерений, воздействием неучтенных случайных факторов;
матрица результатов наблюдений является единственной информацией об изучаемом объекте, имеющейся в распоряжении перед началом исследования.
Функция f(x2 , x3 , …, xт), описывающая зависимость показателя от параметров, называется уравнением (функцией) регрессии. Термин "регрессия" (regression (лат.) – отступление, возврат к чему-либо) связан со спецификой одной из конкретных задач, решенных на стадии становления метода, и в настоящее время не отражает всей сущности метода, но продолжает применяться.
Решение задачи регрессионного анализа целесообразно разбить на несколько этапов:
предварительная обработка ЭД;
выбор вида уравнений регрессии;
вычисление коэффициентов уравнения регрессии;
проверка адекватности построенной функции результатам наблюдений.
Предварительная обработка включает стандартизацию матрицы ЭД, расчет коэффициентов корреляции, проверку их значимости и исключение из рассмотрения незначимых параметров (эти преобразования были рассмотрены в рамках корреляционного анализа). В результате преобразований будут получены стандартизованная матрица наблюдений U (через y будем обозначать стандартизованную величину y* ) и корреляционная матрица .
Стандартизованной матрице U можно сопоставить одну из следующих геометрических интерпретаций:
в т-мерном пространстве оси соответствуют отдельным параметрам и показателю. Каждая строка матрицы представляет вектор в этом пространстве, а вся матрица – совокупность п векторов в пространстве параметров;
в
п-мерном
пространстве оси соответствуют
результатам отдельных наблюдений.
Каждый столбец матрицы – вектор в
пространстве наблюдений. Все вектора
в этом пространстве имеют одинаковую
длину, равную
![]() .
Тогда угол между двумя векторами
характеризует взаимосвязь соответствующих
величин. И чем меньше угол, тем теснее
связь (тем больше коэффициент корреляции).
.
Тогда угол между двумя векторами
характеризует взаимосвязь соответствующих
величин. И чем меньше угол, тем теснее
связь (тем больше коэффициент корреляции).
В корреляционной матрице особую роль играют элементы левого столбца – они характеризуют наличие или отсутствие линейной зависимости между соответствующим параметром ui (i =2, 3, …, т) и показателем объекта y. Проверка значимости позволяет выявить такие параметры, которые следует исключить из рассмотрения при формировании линейной функциональной зависимости, и тем самым упростить последующую обработку.
Выбор вида уравнения регрессии
Задача определения функциональной зависимости, наилучшим образом описывающей ЭД, связана с преодолением ряда принципиальных трудностей. В общем случае для стандартизованных данных функциональную зависимость показателя от параметров можно представить в виде
y = f(u1, u2, ...up) +
где f – заранее не известная функция, подлежащая определению;
- ошибка аппроксимации ЭД.
Указанное уравнение принято называть выборочным уравнением регрессии y на u. Это уравнение характеризует зависимость между вариацией показателя и вариациями факторов. А мера корреляции измеряет долю вариации показателя, которая связана с вариацией факторов. Иначе говоря, корреляцию показателя и факторов нельзя трактовать как связь их уровней, а регрессионный анализ не объясняет роли факторов в создании показателя.
Расчеты для конкретного примера
Для построения без использования специализированных программных продуктов модели парной регрессии, используя статистический материал, приведенный в таблице 4.1, необходимо следующее.
Рассчитать параметры уравнения линейной парной регрессии.
Оценить тесноту связи с помощью показателей корреляции и детерминации.
Используя коэффициент эластичности, определить степень связи факторного признака с результативным.
Определить среднюю ошибку аппроксимации.
Оценить с помощью F-критерия Фишера статистическую надежность моделирования.
Таблица 4.1
|
№ п/п |
Область |
Доля денежных доходов, направленных на прирост сбережений во вкладах, займах, сертификатах и на покупку валюты, в общей сумме среднедушевого денежного дохода, % |
Среднемесячная начисленная заработная плата, у.д.е. |
|
yi |
xi | ||
|
1 |
Калужская |
8,4 |
343 |
|
2 |
Костромская |
6,1 |
356 |
|
3 |
Орловская |
9,4 |
289 |
|
4 |
Рязанская |
11,0 |
341 |
|
5 |
Смоленская |
6,4 |
327 |
|
Итого |
|
41,3 |
1656 |
Для определения неизвестных параметров b0 , b1 уравнения парной линейной регрессии (4.3) используем стандартную систему нормальных уравнений, которая имеет вид:
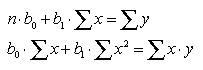 (4.3)
(4.3)
Для решения этой системы вначале необходимо определить значения величин Σ x2 и Σ ху. Эти значения определяем из таблицы исходных данных, дополняя ее соответствующими колонками (табл. 4.2).
Таблица 4.2
Данные для определения Σ x2 и Σ ху
|
№ п/п |
yi |
xi |
x2i |
xi yi |
|
1 |
8,4 |
343 |
117649 |
2881,2 |
|
2 |
6,1 |
356 |
126736 |
2171,6 |
|
3 |
9,4 |
289 |
83251 |
2716,6 |
|
4 |
11,0 |
341 |
116281 |
3751,0 |
|
5 |
6,4 |
327 |
106929 |
2092,8 |
|
Итого |
41,3 |
1656 |
551116 |
13613,2 |
Тогда система (4.3) приобретает вид:
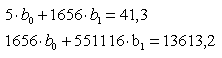 (4.4)
(4.4)
Выражая из первого уравнения b0 и подставляя полученное выражение во второе, получим:
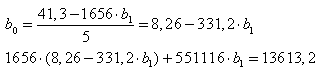
Производя почленное умножение и раскрывая скобки, получим:
![]() .
.
Откуда
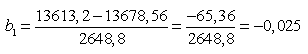 ,
,
тогда
![]() .
.
Окончательно уравнение парной линейной регрессии, связывающее величину доли денежных доходов населения, направленных на прирост сбережений (у), с величиной среднемесячной начисленной заработной платы (х) имеет вид:
![]() (4.5)
(4.5)
Далее, в соответствии с заданием необходимо оценить тесноту статистической связи зависимой переменной у с объясняющей переменной х с помощью показателей корреляции и детерминации.
Так как построено уравнение парной линейной регрессии, то определяем линейный коэффициент корреляции по зависимости:
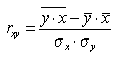 ,
(4.6)
,
(4.6)
где σx, σy — значения среднеквадратических отклонений соответствующих параметров.
Для расчета линейного коэффициента корреляции по зависимости (4.6) выполним промежуточные расчеты:
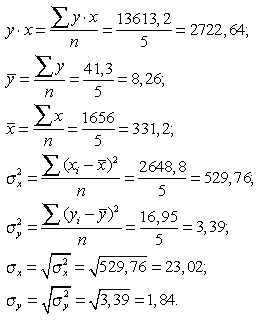
Подставляя значения найденных параметров в выражение (4.6), получим:
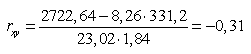 .
.
Полученное значение линейного коэффициента корреляции свидетельствует о наличии слабой обратной статистической связи между величиной доли денежных доходов населения, направленных на прирост сбережений (у), и величиной среднемесячной начисленной заработной платы (х).
Коэффициент детерминации равен:
rxy2 = (-0,31)2 = 0,0961 ,
что означает, что только 9,6% объясняются регрессией объясняющей переменной х на величину у. Соответственно, величина 1 - rxy2 , равная 90,4%, характеризует долю дисперсии переменной у, вызванную влиянием всех остальных, неучтенных в эконометрической модели объясняющих переменных.
Коэффициент эластичности определяется по зависимости (4.5) и равен:
 .
.
Следовательно, при изменении среднемесячной начисленной заработной платы на 1% величина доли денежных доходов населения, направленных на прирост сбережений, также снижается на 1%, причем при увеличении заработной платы наблюдается снижение величины доли денежных доходов населения, направленных на прирост сбережений. Данный вывод противоречит здравому смыслу и может быть объяснен только некорректностью сформированной математической модели.
Для
определения средней ошибки аппроксимации
воспользуемся зависимостью (4.6).
Для удобства расчетов преобразуем
таблицу 4.1 в таблицу 4.3. В данной таблице
в колонке
рассчитаны
текущие значения объясняющей переменной
с использованием зависимости (4.5).
Таблица. 4.3
К расчету средней ошибки аппроксимации
|
№ п/п |
yi |
x i |
|
|
|
1 |
8,4 |
343 |
8,0 |
0,048 |
|
2 |
6,1 |
356 |
7,6 |
0,246 |
|
3 |
9,4 |
289 |
9,3 |
0,011 |
|
4 |
11,0 |
341 |
8,0 |
0,273 |
|
6 |
6,4 |
327 |
8,4 |
0,313 |
|
Итого |
41,3 |
1656 |
41,3 |
0,89 |
Тогда средняя ошибка аппроксимации равна:
 .
.
Полученное значение превышает 12—15%, что свидетельствует о существенности среднего отклонения расчетных данных от фактических, по которым построена эконометрическая модель.
Надежность статистического моделирования выполним на основе F-критерия Фишера. Теоретическое значение критерия Фишера FT определяется из соотношения значений факторной (Dфакторная ) и остаточной (Dост ) дисперсий, рассчитанных на одну степень свободы по формуле:
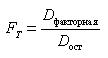 .
(4.7)
.
(4.7)
Промежуточные расчеты (4.7):
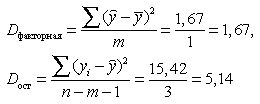
где n — число наблюдений;
m — число объясняющих переменных (для рассматриваемого примера m =1).
Тогда
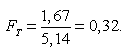
Критическое значение FКРИТ определяется по статистическим таблицам и для уровня значимости α = 0, 05 равняется 10,13. Так как FT <FКРИТ , то нулевая гипотеза не отвергается и полученное уравнение регрессии принимается статистически незначимым.
