Магазинные автоматы

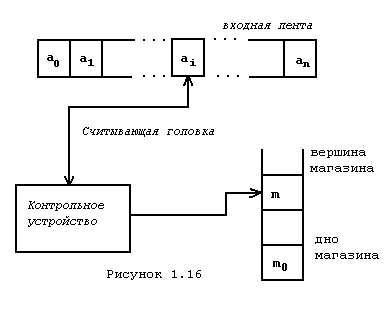
Магазинный автомат - это односторонний в общем случае недетерминированный распознаватель, у которого в качестве вспомогательной памяти используется магазин (рис.1.16). Магазин можно представить в виде строки символов, правый символ которой называют дном магазина, а левый вершиной магазина. Из строки можно считать в определенный момент времени только символ вершины магазина. Причем при считывании символа он удаляется из магазина и вершиной магазина становится следующий (правый) по порядку символ. При записи символов в магазин они помещается слева от вершины магазина и в дальнейшем последний из них рассматривается как новая вершина магазина.

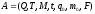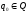Магазинный автомат или автомат с магазинной памятью (МП - автомат) - это семерка , где Q - конечное множество состояний; T - конечный входной алфавит; M - конечный алфавит магазинных символов (стековый алфавит); - начальное состояние автомата; - начальный символ магазина; - конечное множество заключительных состояний; t - функция переходов отображает тройки, образованные состоянием, текущим входным символом на входной ленте или пустым символом и вершиной магазина в множество всех подмножеств 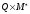. В начале работы на входной ленте записано исходное предложение, ограниченное с двух сторон концевыми маркерами, считывающая головка установлена на первый символ предложения, магазин пуст и содержит начальный символ магазина, магазинный автомат находится в начальном состоянии. В процессе функционирования строка на входной ленте просматривается слева направо без возвратов. На каждом шаге автомат переходит из одной конфигурации в следующую.

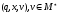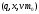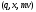Под конфигурацией магазинного автомата понимают тройку - содержимое магазина, - текущее состояние магазинного автомата, - часть исходной строки на входной ленте, начинающаяся с текущего символа (на который указывает считывающая головка) и кончающаяся последним символом строки. Конфигурацию можно также записать в виде или , или , где - символ на вершине магазина. 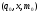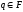Начальная конфигурация в этом случае записывается в виде , заключительная конфигурация - , где и . Для записи перехода автомата из одной конфигурации в другую применяется бинарное отношение ├, определенное на конфигурациях автомата. Будем писать 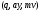├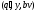, где если пара и . Символ считается допущенным, если автомат читает его из входной строки и переходит из конфигурации в конфигурацию . При этом читающая головка перемещается на один символ вправо и символ m в вершине магазина заменяется строкой магазинных символов b. Если 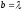, то происходит сокращение содержимого магазина на символ m, при этом в вершине магазина будет содержаться следующий магазинный символ.

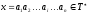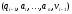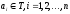Строка символов , где допускается магазинным автоматом, если существует последовательность конфигураций такая, что ├, где . Поскольку разработчиков компиляторов мало интересуют пустые символы в строках, уберем их из определения допускаемой строки. Тогда строка , где , допускается автоматом A, если существует аналогичная строка, допускаемая автоматом A, в которой . Последовательность конфигураций, которые принимает магазинный автомат при распознавании строки x обозначается ├, где . Если конечное состояние магазина совпадает с начальным 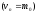, говорят, что строка допускается автоматом A с опустошенным магазином ├

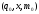Если автомат имеет пустой начальный символ магазина 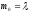, то говорят, что он допускает строку x с пустым магазином. ├

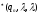
Язык T(A), допускаемый магазинным автоматом, представляет собой множество строк, определяемых формулой и ├

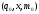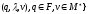
Рассмотренный магазинный автомат позволяет на каждом шаге, либо удалить символ в вершине магазина, либо заменить его строкой магазинных символов конечной длины. Это ограничение снято при определении расширенного магазинного автомата [1], который позволяет заменять строки конечной длины , прилегающие к вершине магазина. Данный магазинный автомат является недетерминированным, поскольку или имеют множество значений (которое может содержать и более одного элемента) и в общем не существует правила для выбора единственного значения из множества. Множество может быть и пустым, тогда автомат не может допускать следующие входные символы.

Описанные выше магазинные автоматы могут применяться в качестве недетерминированных распознавателей контекстно-свободных языков. Доказано, что каждой КС грамматике соответствует магазинный автомат A, такой, что . Недетерминированный магазинный автомат в виде нисходящего распознавателя строится следующим образом. Определим множества, описывающие автомат A. 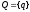- множество состояний; T - входной алфавит состоит из терминальных символов; - алфавит магазинных символов содержит терминальные и нетерминальные символы; - начальное состояние;

- начальный символ магазина; 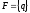- множество конечных состояний.

Функция перехода t определяется следующим образом:

• если множество продукций P содержит правил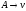о , то 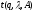содержит 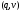для всех продукций с нетерминалом A в левой части;

• для .