
Графы и деревья.
Рассмотрим
мн-во
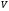 ,
соединенных некоторым образом точек.
Назовем
,
соединенных некоторым образом точек.
Назовем
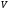 мн-вом вершин, а его элементы
мн-вом вершин, а его элементы
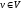 вершинами. Направленным графом
вершинами. Направленным графом
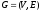 называется совокупность конечного
мн-ва вершин и определенного на этом
мн-ве отношения
называется совокупность конечного
мн-ва вершин и определенного на этом
мн-ве отношения
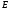 .
Направленный граф можно представить
графически следующим образом. Расположим
на листе бумаги все вершины мн-ва
.
Направленный граф можно представить
графически следующим образом. Расположим
на листе бумаги все вершины мн-ва
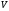 .
Каждую вершину изобразим в виде
окружности, внутри которой вписан
элемент множества
.
Каждую вершину изобразим в виде
окружности, внутри которой вписан
элемент множества
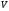 .
Две вершины
.
Две вершины
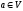 и
и
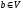 соединим отрезком линии, если существует
пара
соединим отрезком линии, если существует
пара
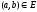 .
В этом случае будем говорить, что граф
.
В этом случае будем говорить, что граф
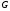 содержит ребро
содержит ребро
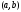 .
.
Если
в графе имеется некоторая последовательность
вершин
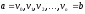 ,
где
,
где
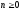 и
и
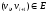 для
для
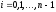 ,
говорят, что в графе существует путь
длиной
,
говорят, что в графе существует путь
длиной
 из вершины
из вершины
 в вершину
в вершину
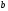 .
Для
.
Для
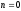
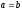 .
Граф
.
Граф
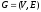 может содержать подграфы вида
может содержать подграфы вида
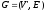 ,
если
,
если
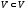 и
и
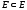 .
Два подграфа, не имеющие общих вершин,
называются раздельными подграфами.
.
Два подграфа, не имеющие общих вершин,
называются раздельными подграфами.
Рекурсивное
определение дерева. Деревом
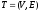 называют такой направленный граф,
который имеет либо одну единственную
вершину, называемую корнем
называют такой направленный граф,
который имеет либо одну единственную
вершину, называемую корнем
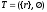 ,
либо совокупность корня, нескольких
раздельных подграфов-деревьев
,
либо совокупность корня, нескольких
раздельных подграфов-деревьев
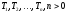 и ребер от корня дерева
и ребер от корня дерева
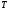 до вершин-корней деревьев
до вершин-корней деревьев
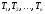 .
Дерево представляют в виде расположенного
вверху корня и направленных сверху вниз
ребер. В этом случае можно не указывать
направление ребер. Вершину дерева из
которой не выходит ни одного ребра
называют листом, остальные вершины -
внутренними вершинами дерева.
.
Дерево представляют в виде расположенного
вверху корня и направленных сверху вниз
ребер. В этом случае можно не указывать
направление ребер. Вершину дерева из
которой не выходит ни одного ребра
называют листом, остальные вершины -
внутренними вершинами дерева.
Строки.
Под
строкой всегда понимается некоторая
последовательность символов
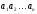 ,
каждый из которых принадлежит некоторому
конечному алфавиту
,
каждый из которых принадлежит некоторому
конечному алфавиту
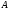 .
В дальнейшем для обозначения отдельных
символов будем использовать строчные
буквы
.
В дальнейшем для обозначения отдельных
символов будем использовать строчные
буквы
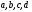 ,
а для обозначения строк - буквы
,
а для обозначения строк - буквы
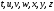 .
Строка, состоящая из
.
Строка, состоящая из
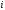 символов
символов
 ,
будет обозначаться
,
будет обозначаться
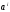 .
Длина произвольной строки
.
Длина произвольной строки
 представляет собой число символов в
строке и обозначается. В общем случае
существует пустая строка
представляет собой число символов в
строке и обозначается. В общем случае
существует пустая строка
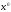 ,
которая имеет нулевую длину
,
которая имеет нулевую длину
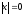 и обозначается
и обозначается
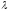 .
.
Формально
строки символов в алфавите
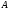 определяются следующим образом:
определяются следующим образом:
-
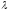 -
строка в
-
строка в
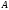 ;
; -
если
 - строка в
- строка в
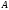 и
и
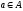 ,
то
,
то
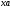 - строка в
- строка в
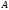 ;
; -
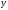 -
строка тогда и только тогда, когда она
является таковой в силу первых двух
положений.
-
строка тогда и только тогда, когда она
является таковой в силу первых двух
положений.
Если
 и
и
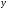 строки, то строка
строки, то строка
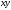 называется конкатенацией (сцеплением
или объединением)
называется конкатенацией (сцеплением
или объединением)
 и
и
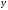 .
Причём
.
Причём
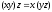 ,
но
,
но
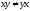 .
Для пустой строки справедливо следующее
утверждение
.
Для пустой строки справедливо следующее
утверждение
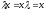 для любого
для любого
 .
Обращением строки
.
Обращением строки
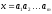 называется строка, записанная в обратном
порядке
называется строка, записанная в обратном
порядке
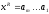 .
.
Пусть
 ,
,
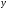 и
и
 произвольные строки в некотором алфавите
произвольные строки в некотором алфавите
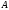 и строка
и строка
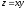 ,
тогда строка
,
тогда строка
 называется префиксом строки
называется префиксом строки
 ,
а строка
,
а строка
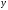 -
суффиксом строки
-
суффиксом строки
 .
.
Формальные языки.
Обозначим
через
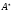 множество определенных над алфавитом
множество определенных над алфавитом
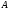 строк. Например, для
строк. Например, для
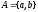
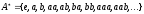
Множество
всех строк в
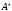 за исключением
за исключением
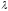 обозначается
обозначается
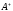 .
Таким образом
.
Таким образом
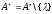 .
.
Формальным
языком
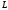 над алфавитом
над алфавитом
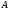 называется произвольное подмножество
множества
называется произвольное подмножество
множества
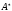 .
Пусть
.
Пусть
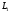 и
и
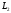 - два формальных языка, тогда их
конкатенация (объединение)
- два формальных языка, тогда их
конкатенация (объединение)
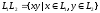 также является формальным языком.
Например, для языков
также является формальным языком.
Например, для языков
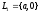 и
и
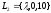 ,
,
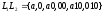 .
Конкатенация формального языка
.
Конкатенация формального языка
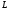 с самим собой записывается в виде
с самим собой записывается в виде
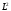 .
В общем случае это выглядит так
.
В общем случае это выглядит так
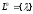 ,
,
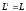 ,
,
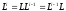 для
для
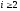 .
Тогда
.
Тогда
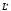 можно определить как
можно определить как
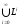 ,
а
,
а
