Конечные автоматы
Конечный
автомат представляет собой пятерку

где,
Q - конечное множество состояний автомата,
T - непустое конечное множество входных
символов, входной алфавит,
 - начальное состояние,
- начальное состояние,
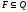 - непустое множество заключительных
состояний автомата, t-
переходная функция
- непустое множество заключительных
состояний автомата, t-
переходная функция

Такой
автомат работает как распознаватель
следующим образом (рис.1.11). На ленте
записана входная строка, ограниченная
с двух сторон концевыми маркерами.
Управляющее устройство находится в
начальном состоянии
 .
Входная лента последовательно
просматривается слева направо по одному
символу. Допустим, что с помощью
считывающей головки оказались просмотрены
символы
.
Входная лента последовательно
просматривается слева направо по одному
символу. Допустим, что с помощью
считывающей головки оказались просмотрены
символы
 и управляющее устройство находится в
состоянии
и управляющее устройство находится в
состоянии
 .
Символ
.
Символ
 допускается, если существует хотя бы
одно состояние
допускается, если существует хотя бы
одно состояние
 .
.

Если такого состояния не существует, автомат останавливает свою работу. В общем случае таких состояний может быть несколько, и распознаватель будет недетерминированным, т.е. речь в этом случае будет идти о недетерминированном конечном автомате.
Строка
 допускается автоматом, если существует
последовательность состояний
допускается автоматом, если существует
последовательность состояний
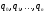 ,
такая, что
,
такая, что
 ,
где
,
где
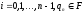 и после прочтения последнего символа
и после прочтения последнего символа
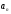 строки был встречен концевой маркер.
Предполагается, что начальный маркер
читается в состоянии
строки был встречен концевой маркер.
Предполагается, что начальный маркер
читается в состоянии
 .
Этот факт можно записать с помощью
функции перехода следующим образом
.
Этот факт можно записать с помощью
функции перехода следующим образом
 .
В этом случае функцию перехода,
соответствующую одному такту работы
распознавателя, можно рассматривать
как частный случай ее общей формы записи
для строки x содержащей один символ
.
В этом случае функцию перехода,
соответствующую одному такту работы
распознавателя, можно рассматривать
как частный случай ее общей формы записи
для строки x содержащей один символ
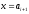 и состояния
и состояния
 .
Таким образом, функцию t можно определить
рекурсивно
.
Таким образом, функцию t можно определить
рекурсивно
 ,
если строка
,
если строка
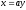 ,
где
,
где
 и
и
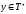 .
.
Множество
всех строк T(A), допускаемых автоматом
A, может быть записано в виде

Если
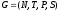 праволинейная грамматика, то существует
конечный автомат такой, что
праволинейная грамматика, то существует
конечный автомат такой, что
 .
Этот автомат строится из грамматики
следующим образом. Множество состояний
можно получить объединением множества
нетерминальных символов и специально
введенного конечного состояния
.
Этот автомат строится из грамматики
следующим образом. Множество состояний
можно получить объединением множества
нетерминальных символов и специально
введенного конечного состояния
 ,
т.е.
,
т.е.
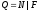 .
Соответственно начальное состояние
совпадет с начальным символом грамматики
.
Соответственно начальное состояние
совпадет с начальным символом грамматики
 .
В качестве входного алфавита используется
множество терминальных символов T.
Определим функцию перехода для каждой
продукции грамматики.
.
В качестве входного алфавита используется
множество терминальных символов T.
Определим функцию перехода для каждой
продукции грамматики.
 ,
если существует правило
,
если существует правило
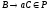 и
и
 ;
;
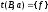 ,
если существует правило
,
если существует правило
 ;
;
 во
всех остальных случаях.
во
всех остальных случаях.
Таким образом, число элементов области определения функции переходов, для которых ее значение не пустое множество, в точности равно числу продукций в грамматике.
Практика
показала, что одним из удобных способов
задания функции переходов является
граф переходов или его еще называют
граф состояний. Граф состояний
 является направленным графом и строится
следующим образом. Каждому состоянию
множества Q соответствует одна вершина
множества V.
является направленным графом и строится
следующим образом. Каждому состоянию
множества Q соответствует одна вершина
множества V.
Все
вершины, кроме заключительных, обозначаются
на рисунках в виде окружностей. На
начальную вершину, соответствующую
начальному состоянию автомата, указывает
стрелка. Заключительная вершина
изображается прямоугольником. Ребро
 существует на графе, если для символа
существует на графе, если для символа
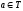 и состояния
и состояния
 значение функции
значение функции
 t(B,a)
не пусто и равно
t(B,a)
не пусто и равно
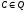 .
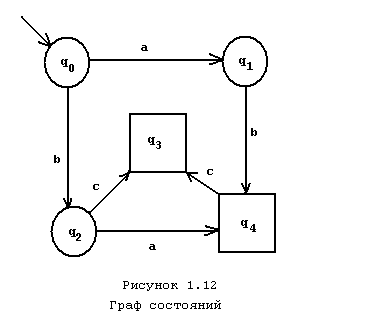
На рис. 1.12 изображен граф состояний
автомата A.
.
На рис. 1.12 изображен граф состояний
автомата A.
 ,
где
,
где
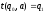

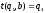

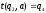
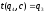
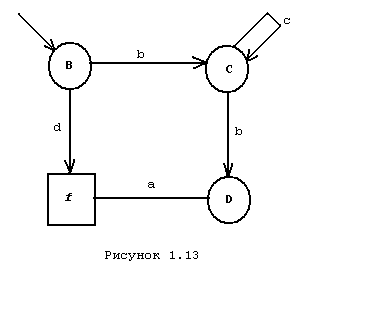
Граф
состояний автомата, построенного на
основе праволинейной грамматики
 ,
показан на рис. 1.13. Покажем соответствие
между продукциями грамматики G и
элементами функции перехода автомата.
,
показан на рис. 1.13. Покажем соответствие
между продукциями грамматики G и
элементами функции перехода автомата.
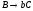
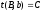
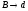

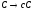



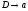

где f - заключительное состояние автомата.