
Формальные грамматики.
синтаксис - определения, которые точно устанавливают какие строки имеют смысл в данном языке(для его описания ф-лы Бэкуса - Наура и синтаксические диаграммы, формальные грамматики.). семантика языка - правила интерпретации синтаксических определений, задающие смысл допустимым конструкциям языка. Грамматика - математическая система, порождающая язык. Строки языка строятся способом, точно определенным правилами грамматики.
Формальная
грамматика
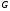 - это четверка
- это четверка
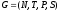 где
где
 - конечное мн-во нетерминалов;
- конечное мн-во нетерминалов;
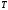 - конечное мн-во терминалов,
- конечное мн-во терминалов,
 ;
;
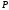 - конечное мн-во правил-продукций вида
- конечное мн-во правил-продукций вида
 ,
где
,
где
 - строка левой части продукции
- строка левой части продукции
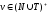 ,
,
 - строка правой части продукции
- строка правой части продукции
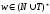 ,
,
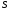 - начальный символ грамматики
- начальный символ грамматики
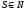 .
Символ
.
Символ
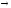 в продукции
в продукции
 означает возможность замены строки
означает возможность замены строки
 на строку
на строку
 .
.
Грамматика
рекурсивным образом определяет
порождаемый язык, который содержит
мн-во выводимых из начального символа
строк. Строка
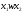 называется выводимой
строкой
грамматики
называется выводимой
строкой
грамматики
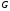 ,
если
,
если
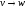 продукция из множества
продукция из множества
 и
и
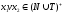 строка терминальных и нетерминальных
символов длиной 1. Выводимая строка
получается путем замены строки
строка терминальных и нетерминальных
символов длиной 1. Выводимая строка
получается путем замены строки
 на строку
на строку
 в строке
в строке
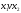 .
Такое преобразование строки записывают
в виде
.
Такое преобразование строки записывают
в виде
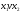

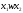 .
Преобразование
.
Преобразование
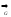 можно рассматривать как отношение на
множестве
можно рассматривать как отношение на
множестве
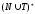 .
Это отношение является рефлексивным,
так как допустима замена строки
.
Это отношение является рефлексивным,
так как допустима замена строки
 на самое себя. Однако оно определено не
для всех элементов
на самое себя. Однако оно определено не
для всех элементов
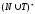 ,
нетранзитивно и несимметрично.
,
нетранзитивно и несимметрично.
Отношение
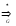 на множестве
на множестве
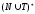 задается как
задается как
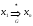 ,
если существует последовательность
,
если существует последовательность
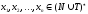 для
для
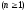 и
и
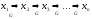 .
В этом случае говорят, что строка
.
В этом случае говорят, что строка
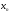 выводится из строки
выводится из строки
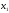 за один более шагов. Отношение
за один более шагов. Отношение
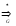 рефлексивно
и транзитивно, но несимметрично.
рефлексивно
и транзитивно, но несимметрично.
Если
строка
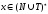 является выводимой из начального символа
строкой (
является выводимой из начального символа
строкой (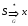 ),
то ее называют сентенциальной
формой.
),
то ее называют сентенциальной
формой.
Не
содержащая нетерминальных символов
сентенциальная форма называется
предложением
(или сентенцией).
Множество всех предложений грамматики
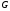 называют языком, порождаемым этой
грамматикой и обозначают
называют языком, порождаемым этой
грамматикой и обозначают
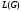 .
Таким образом
.
Таким образом
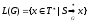
Если
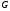 и
и
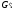 порождают один и тот же язык
порождают один и тот же язык
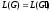 .
О таких грамматиках говорят, что они
эквивалентны.
.
О таких грамматиках говорят, что они
эквивалентны.
Классификация грамматик.
Грамматика
 называется :
называется :
праволинейной
или автоматной
(тип 3), если
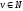 ,
,
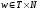 или
или
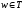 ,
т.е. каждое правило из множества продукций
,
т.е. каждое правило из множества продукций
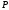 имеют вид
имеют вид
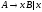 ,
где
,
где
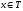 и
и
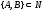
контекстно-свободной
(тип
2), если
 ,
,
 ;
;
контекстно-зависимой
неукорачивающей
(тип 1), если
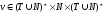 ,
,
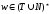 и длина строки
и длина строки
 не превышает длину строки
не превышает длину строки

 ;
;
контекстно-зависимой
без ограничений
(тип 0), если
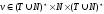 ,
,
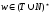 .
.
Язык,
порождаемый грамматикой типа
 ,
называется языком типа
,
называется языком типа
 .
.
Определенные
выше четыре типа языков и грамматик
называют иерархией Хомского. В приведенном
определении контекстно-свободной
грамматики недопустимыми являются так
называемые
 -
продукции, продукции вида
-
продукции, продукции вида
 .
Однако многие авторы включают такие
продукции в число допустимых продукций
контекстно-свободных грамматик, а
контекстно-свободные грамматики без
.
Однако многие авторы включают такие
продукции в число допустимых продукций
контекстно-свободных грамматик, а
контекстно-свободные грамматики без
 -
продукций называют
-
продукций называют
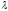 -свободными
грамматиками. Конечно при разработке
трансляторов более удобно использовать
именно такие грамматики без
-свободными
грамматиками. Конечно при разработке
трансляторов более удобно использовать
именно такие грамматики без
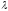 -
продукций. Но и при наличии в грамматике
-
продукций. Но и при наличии в грамматике
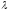 -
продукции ситуация не является
безнадежной, поскольку доказано, что
для любого контекстно-свободного языка
-
продукции ситуация не является
безнадежной, поскольку доказано, что
для любого контекстно-свободного языка
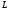 существует
существует
 -
свободная контекстно-свободная грамматика
-
свободная контекстно-свободная грамматика
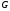 ,
такая, что
,
такая, что
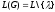 .
Построение такой грамматики несложно.
.
Построение такой грамматики несложно.
С точки зрения приложений к языкам программирования наиболее подходящими являются контекстно-свободные грамматики. Это связано с тем, что с помощью этих грамматик удается достаточно полно описать синтаксис существующих языков программирования. С точки зрения трансляции наиболее важным вопросом, на который необходимо иметь ответ, является вопрос о наличии нескольких выводов из начального символа одного и того же предложения языка.
Для
представления вывода
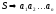 ,
где
,
где
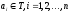 обычно используется дерево вывода.
Вершины дерева помечены символами из
множества
обычно используется дерево вывода.
Вершины дерева помечены символами из
множества
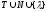 .
Корнем дерева является вершина, помеченная
начальным символом
.
Корнем дерева является вершина, помеченная
начальным символом
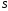 ,
а листьями вершины с терминальными
символами. Все промежуточные вершины
дерева помечены нетерминалами множества
,
а листьями вершины с терминальными
символами. Все промежуточные вершины
дерева помечены нетерминалами множества
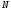 .
.
Схема
вывода предложения
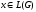 называется левосторонней(правосторонней),
если подстановка очередного правила
осуществляется всегда на место самой
левой (правой) сентенциальной формы.
называется левосторонней(правосторонней),
если подстановка очередного правила
осуществляется всегда на место самой
левой (правой) сентенциальной формы.
Контекстно-свободную
грамматику, в которой все возможные
схемы выводов строки
 соответствуют одному и тому же дереву
вывода будем называть однозначной..
соответствуют одному и тому же дереву
вывода будем называть однозначной..
