
Множества
Множество - это набор несовпадающих объектов. Объекты обозначаются своими именами и называются элементами множества. Если множество содержит конечное число элементов, то его можно задать простым перечислением имен объектов.
Задать
множество простым перечислением можно,
когда оно содержит конечное число
элементов. Для задания бесконечных
множеств используется некоторое общее
свойство, которым должен обладать
объект, чтобы стать элементом данного
множества. Такое общее свойство записывают
в виде утверждения (предиката), содержащего
одну или несколько переменных. Предикат
может принимать одно из двух значений
- истина или ложь. В этом случае множество
состоит из тех элементов, для которых
предикат истинен. Выбирать предикат
необходимо осторожно, поскольку может
оказаться, что определяемое множество
не существует (парадокс Рассела). Примером
бесконечного множества может служить
множество
 ,
содержащее целые числа.
,
содержащее целые числа. -простое число
-простое число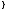 Переменная
Переменная
 ,
принимает значения из заданного множества
и может быть целым числом.
,
принимает значения из заданного множества
и может быть целым числом.
Может
оказаться так, что множество не имеет
ни одного элемента (предикат принимает
значения ложь для всех значений
переменных). Такое множество называют
пустым множеством и обозначают
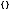 или
или
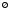 .
Множества могут быть элементами других
множеств, которые называют системами
множеств и обозначают
.
Множества могут быть элементами других
множеств, которые называют системами
множеств и обозначают
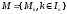 ,
где
,
где
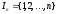
Говорят,
что множество
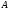 содержится в множестве
содержится в множестве
 и пишут
и пишут
 ,
если каждый элементмножества
,
если каждый элементмножества
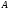 является элементом множества
является элементом множества
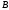 .
В этом случае множество
.
В этом случае множество
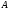 называют подмножеством множества
называют подмножеством множества
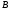 .
Если существует элемент
.
Если существует элемент
 ,
который не принадлежит
,
который не принадлежит

 ,
то множество
,
то множество
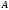 не является подмножеством множества
не является подмножеством множества
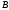 ,
что записывают в виде
,
что записывают в виде
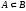 .
Следует отметить, что пустое множество
содержится в любых других множествах
.
Следует отметить, что пустое множество
содержится в любых других множествах
 ,
,
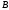 .
.
Два
множества
 и
и
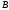 называются равными
называются равными
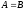 ,
если
,
если
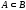 и
и
 .
.
Таким
образом, множества
 и
и
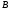 являются равными, если они совпадают
или другими словами содержат одни и те
же элементы.
являются равными, если они совпадают
или другими словами содержат одни и те
же элементы.
Из
множеств при помощи определенных
операций можно образовывать новые
множества. К основным операциям над
множествами относятся объединение
 ,
пересечение
,
пересечение
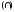 ,
вычитание
,
вычитание
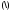 ,
дополнение
,
дополнение
 .
Предположим, что
.
Предположим, что
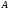 и
и
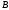 подмножества некоторого универсального
множества
подмножества некоторого универсального
множества
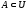 и
и
 .
Тогда основные операции можно определить
следующим образом:
.
Тогда основные операции можно определить
следующим образом:
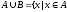 или
или
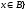 - объединение множеств, состоит из всех
элементов, принадлежащих, по крайней
мере одному из множеств
- объединение множеств, состоит из всех
элементов, принадлежащих, по крайней
мере одному из множеств
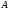 или
или
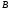 ;
;
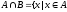 и
и
 - пересечение множеств, состоит из всех
элементов, относящихся одновременно к
обоим множествам
- пересечение множеств, состоит из всех
элементов, относящихся одновременно к
обоим множествам
 и
и
 ;
;
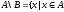 ,но
,но
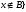 -
вычитание множеств, содержит все элементы
множества
-
вычитание множеств, содержит все элементы
множества
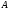 ,
которые не являются элементами множества
,
которые не являются элементами множества
 ;
;
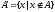 или
или
 дополнение, охватывает все те элементы
множества
дополнение, охватывает все те элементы
множества
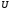 ,
которые не являются элементами множества
,
которые не являются элементами множества
 .
.
Для
любых множеств
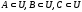 выполняются
следующие законы [2]:
выполняются
следующие законы [2]:
1) Ассоциативный закон:


2) Коммутативный закон:

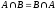
3) Закон о дополнении:

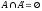
4) Закон идемпотенции:
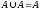

5) Закон эквивалентности:
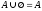
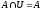
6) Закон существования пустого множества:

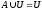
7) Закон инволюции:
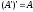
8) Закон Моргана:


9) Дистрибутивный закон:
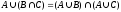
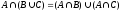
Поскольку
операции объединения и пересечения
множеств ассоциативны, их можно применять
для последовательности множеств
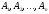 .
.
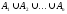 или
или

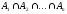 или
или
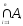 .
Особое место среди операций над
множествами занимает прямое (декартово)
произведение множеств. Под произведением
множеств
.
Особое место среди операций над
множествами занимает прямое (декартово)
произведение множеств. Под произведением
множеств
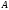 и
и
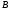 ,
обозначаемым через
,
обозначаемым через
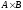 ,
понимают множество
,
понимают множество
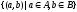 ,
состоящее из упорядоченных пар объектов.
Первый объект пары является элементом
множества
,
состоящее из упорядоченных пар объектов.
Первый объект пары является элементом
множества
 ,
второй - элементом множества
,
второй - элементом множества
Отметим,
что в общем случае
 ,
но
,
но
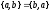 .
Аналогично можно определить произведение
трех и более множеств.
.
Аналогично можно определить произведение
трех и более множеств.
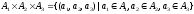

В
частности можно рассматривать произведение
 одинаковых множеств
одинаковых множеств

Любое
подмножество множества
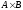 есть
отношение, при этом множество
есть
отношение, при этом множество
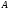 называют областью определения, а
множество
называют областью определения, а
множество
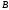 -
областью значений. Область определения
и область значений могут быть одним и
тем же множеством. Если
-
областью значений. Область определения
и область значений могут быть одним и
тем же множеством. Если
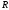 отношение из
отношение из
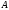 в
в
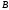 и
и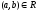 ,
то пишут
,
то пишут
 .
.
Отношение
 на множестве
на множестве
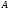 называют: рефлексивным , если
называют: рефлексивным , если
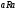 выполняется для всех
выполняется для всех
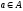 ;
симметричным , если из
;
симметричным , если из
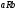 всегда следует
всегда следует
 ;
транзитивным , если из
;
транзитивным , если из
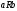 и
и
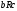 всегда следует
всегда следует
 .(
отношения эквивалентности)
.(
отношения эквивалентности)
Функция(отображение)
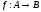 есть отношение, определенное на множестве
есть отношение, определенное на множестве
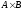 и представляющее собой множество пар
и представляющее собой множество пар
 ,
где
,
где
 и
и
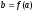 ,
причем, если
,
причем, если
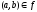 и
и
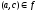 ,
то
,
то
 .
Такие функции называют однозначными.
Если функция определена на всех элементах
множества
.
Такие функции называют однозначными.
Если функция определена на всех элементах
множества
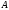 ,
то ее называют полной. Полная функция
будет взаимно однозначной , если из
того, что
,
то ее называют полной. Полная функция
будет взаимно однозначной , если из
того, что
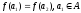 и
и
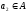 следует, что
следует, что
 .
Между множествами
.
Между множествами
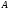 и
и
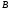 может быть установлено взаимно однозначное
соответствие, если существует полная
взаимно однозначная функция
может быть установлено взаимно однозначное
соответствие, если существует полная
взаимно однозначная функция
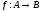 .
.
