5. Полная модель Гумеля-Пуна

При отказе от допущений раздела 4 в неравновесном состоянии

, т.е._.

При этом в формулах для определения токов I_e1иI_с1нуждается в определении полный заряд дырок в базе:

где , (3.6а), (3.6б)

Метод Гуммеля-Пуна позволяет найти этот заряд функцию от напряжений на р-ппереходах:

,.или.

Процедура нахождения этой функции поясняется рисунком 5.1 (он же 3.1).

, (4.1)

где — избыточная концентрация дарок в активной базе.

Первое слагаемоев правой части (4.1) можно представить в следующем виде:

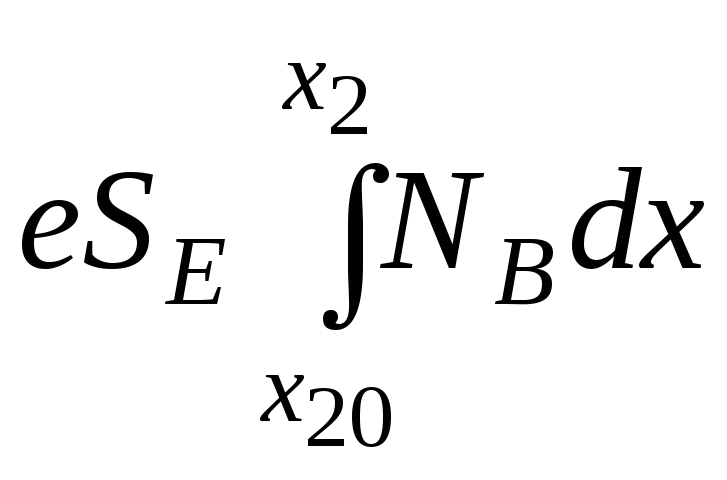. (4.2)

Интегралы в правой части (4.2) имеют следующий физический смысл:

— (4.3а)

равновесный заряд дырок в активной базе;

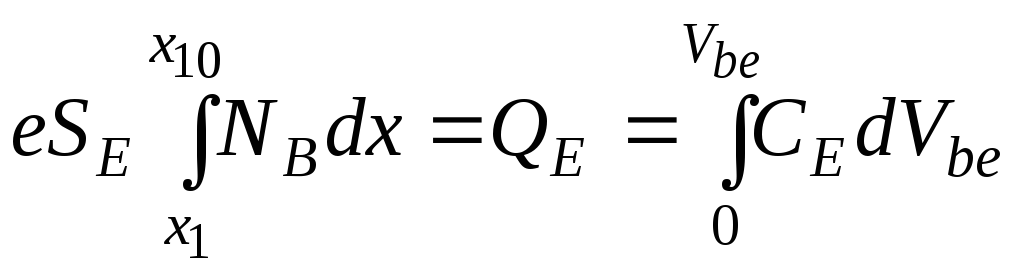— (4.3б)

заряд вбарьерной емкостиэмиттерного перехода;

— (4.3в)

заряд в барьерной емкостиактивной части коллекторного перехода.

Поскольку в интервале база электронейтральна (),второе слагаемоев правой части (4.1) соответствует заряду вдиффузионной емкости базы:

.

Этот заряд является суммой зарядов электронов, пролетающих через активную базу в прямом направлении за время T_F(создающих токI_e1) и электронов, пролетающих через базу в обратном направлении за времяT_R(создающих токI_с1). Поэтому

. (4.4)

Подставляя (4.3а-в) в (4.2), а затем (4.2) и (4.4) в (4.1), получим:

. (4.5)

В уравнении (4.5) функции определены уравнениями (3.6а,б) и (3.7а,б). После их подстановки получим квадратное уравнение относительно заряда(или), которое имеет следующее решение:

,

или, (4.6)

где , (4.7а). (4.7б)

Алгоритм вычислений, которые производятся при компьютерном моделировании на каждом временном шаге, имеет следующий вид:

Таким образом, для описания статических характеристик должны быть заданы следующие параметры:

I_ns , Q_B0 , I_KF , I_KR , B_F , B_R ,

параметры ВФХ барьерных емкостей С_E (V_be), С_C (V_bc),

и параметры ВАХ диодов I_ep (V_be), I_cp (V_bc), I_erg (V_be), I_crg (V_bc)и I_c2 (V_bc).

Для транзисторов с малыми топологическими размерами ВАХ диодов должны включать токи, протекающие через боковые периферийные поверхности р-ппереходов.

Механизм учета эффекта Эрли.

В нормальном режиме работы () в пренебрежении обратными токами через коллекторный переход

.

Зависимость коллекторного тока от напряжения (эффект Эрли) в модели Г-П отражена зависимостьюв формуле (4.6):

.

Таким же образом зависимость учитывает эффект Эрли в инверсном включении.

Для ускорения вычислений и облегчения процедуры экспериментальной верификации параметров модели вместо (4.6) используется приближенное соотношение

. (4.6а)

Здесь эффект Эрли учтен параметрами V_AFиV_AR , которые называютсяпрямым и инверсным напряжениями Эрли. Смысл и способ измерения прямого напряжения ЭрлиV_AFпоясняется рисунком 5.2.

Наклон ВАХ при -V_bc > 0

утрирован